Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 34.18 Профильный Уровень Мордкович — Подробные Ответы
Изобразите на комплексной плоскости множество всех тех чисел, у которых аргумент:
а) Положителен
б) Отрицателен
в) Больше чем
г) Меньше чем
Изобразить на комплексной плоскости множество всех тех чисел, у которых аргумент:
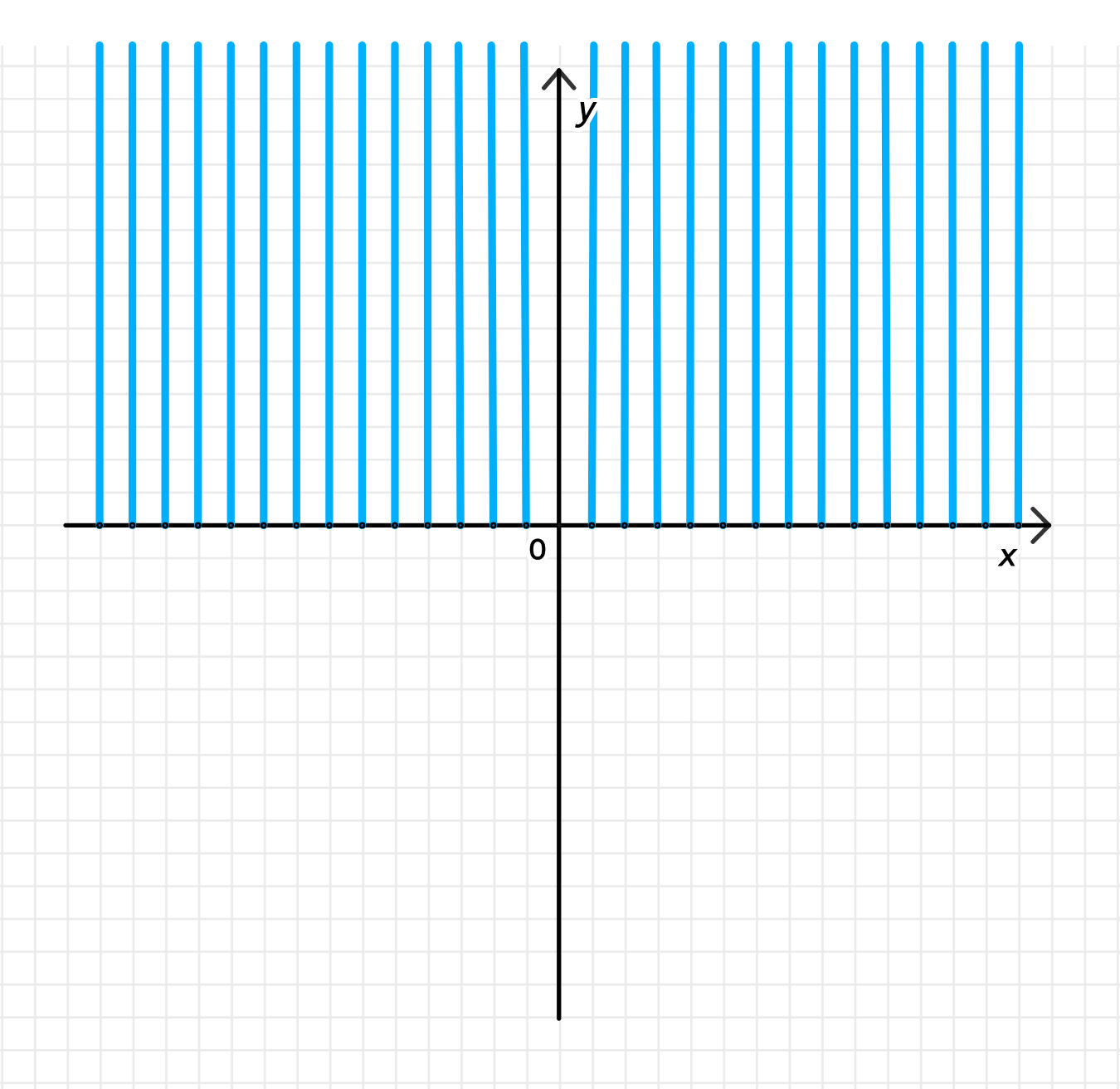
а) Положителен:
;
;
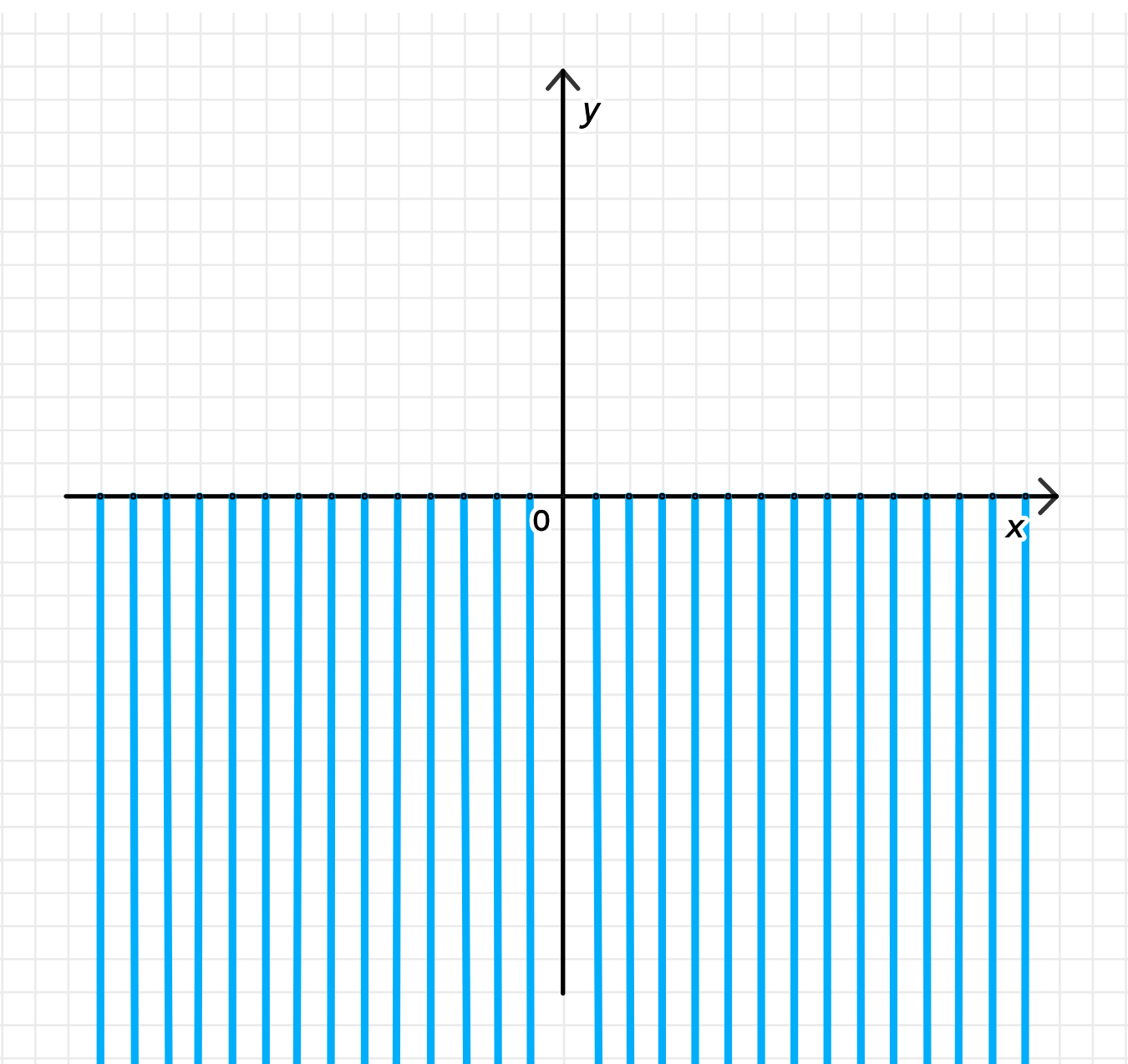
б) Отрицателен:
;
;
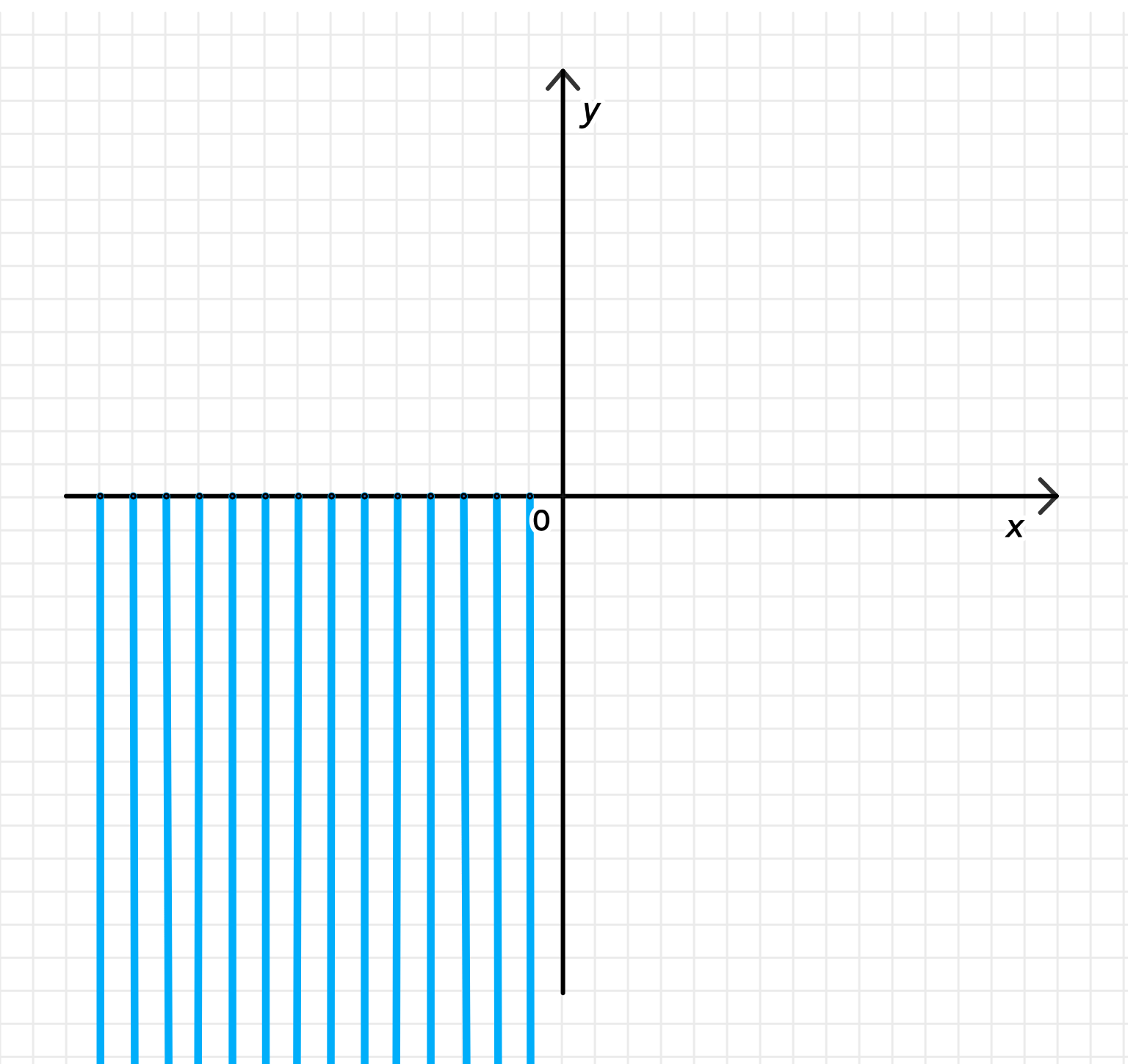
в) Больше чем :
;
;
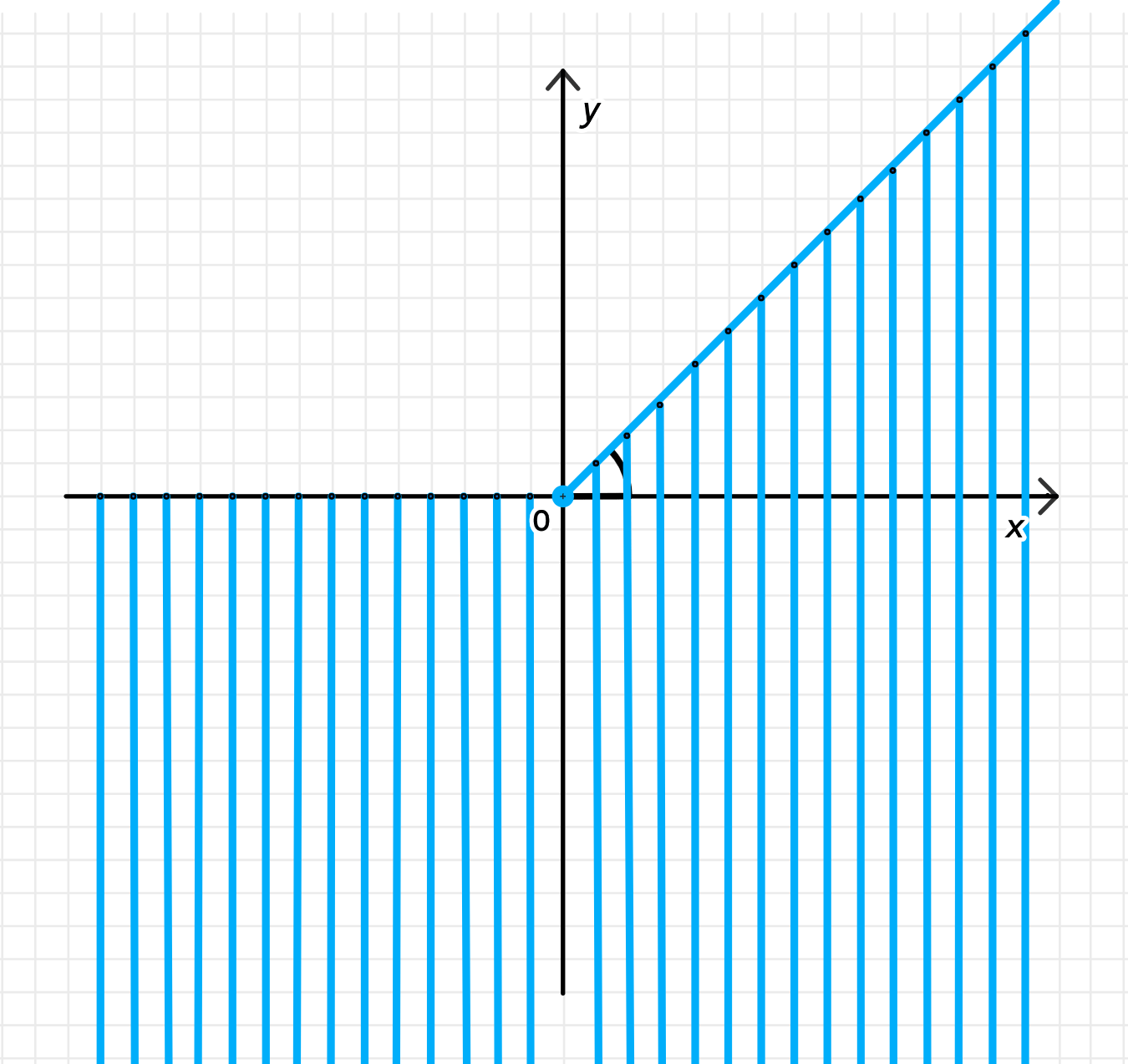
г) Меньше чем :
;
;
Изобразить на комплексной плоскости множество всех комплексных чисел , для которых аргумент (угол между положительной частью оси абсцисс и вектором ) принадлежит указанному промежутку.
Комплексное число:
Геометрически представляется точкой или вектором от начала координат до этой точки.
Аргумент числа :
Измеряется в радианах или градусах.
а) Аргумент положителен:
Пояснение:
- Угол больше нуля — значит, вектор лежит выше положительной части оси .
- Верхняя полуплоскость (включая ось , кроме положительной оси , которая соответствует ).
Геометрически:
- Вся верхняя полуплоскость, исключая положительную часть оси (т.е. точек вида ).
- Включается: 1-я и 2-я четверти.
- Граница: включена ось , включена отрицательная часть Ox, исключена положительная часть Ox.
б) Аргумент отрицателен:
Пояснение:
- Аргумент меньше нуля — значит, вектор находится ниже оси , но не на ней.
Геометрически:
- Вся нижняя полуплоскость, исключая ось (где аргумент = 0 или ).
- Включается: 3-я и 4-я четверти.
- Не включаются: положительная и отрицательная часть оси .
в) Аргумент больше :
Пояснение:
- Это часть 2-й четверти, от вертикали вверх (ось , не включается) до отрицательной оси (включается).
- Угол от до , т.е. от вертикали налево вверх.
Геометрически:
- Все точки, образующие угол между и .
- Это внутренность 2-й четверти, включая отрицательную часть оси , но исключая ось .
- Область лежит между лучами: от (ось ) до (отрицательная часть ).
г) Аргумент меньше :
Пояснение:
- Это все углы ниже , включая всю нижнюю полуплоскость и часть верхней (до 45°).
Геометрически:
- Объединение:
- Вся нижняя полуплоскость (углы ).
- Часть верхней полуплоскости, в пределах от до — т.е. небольшой сектор в 1-й четверти, между положительной осью и лучом с углом .
- Исключаются:
- Угол (т.е. ), так как он больше чем .
- Угол не включён (неравенство строгое).
- Ось полностью исключена (на ней аргумент равен ).