ГДЗ по Алгебре 10 Класс Номер 34.20 Профильный Уровень Мордкович — Подробные Ответы

Изобразите на комплексной плоскости множество всех тех чисел $z$, у которых:

а) $\frac{\pi}{2} < \arg(z) < \frac{3\pi}{4}$ и $|z| = 2$;

б) $\frac{\pi}{2} < \arg(z) < \frac{3\pi}{4}$ и $3 < |z| < 5$;

в) $-\frac{3\pi}{4} < \arg(z) < \frac{\pi}{6}$ и $|z| = 8$;

г) $-\frac{5\pi}{6} < \arg(z) < \frac{2\pi}{3}$ или $1 < |z| < 2$.

Изобразить на комплексной плоскости множество всех тех чисел $z$, у которых:

а)

$$\frac{\pi}{2} < \arg(z) < \frac{3\pi}{4} \quad \text{и} \quad |z| = 2;$$ $$90^\circ < a < 135^\circ \quad \text{и} \quad R = 2;$$

б)

$$\frac{\pi}{2} < \arg(z) < \frac{3\pi}{4} \quad \text{и} \quad 3 < |z| < 5;$$ $$90^\circ < a < 135^\circ \quad \text{и} \quad 3 < R < 5;$$

в)

$$-\frac{3\pi}{4} < \arg(z) < \frac{\pi}{6} \quad \text{и} \quad |z| = 8;$$ $$-135^\circ < a < 30^\circ \quad \text{и} \quad R = 8;$$

г)

$$-\frac{5\pi}{6} < \arg(z) < \frac{2\pi}{3} \quad \text{или} \quad 1 < |z| < 2;$$ $$-{150}^{\circ }<a<{120}^{\circ }\text{или}1<R<2;$$

$$-150^\circ < a < 120^\circ \quad \text{или} \quad 1 < R < 2;$$

Нам необходимо изобразить на комплексной плоскости множество всех чисел $z$, которые удовлетворяют заданным условиям для различных случаев (а), б), в), г)).

Для этого рассмотрим каждый случай отдельно. Мы будем использовать полярную форму комплексного числа для точности описания каждой области.

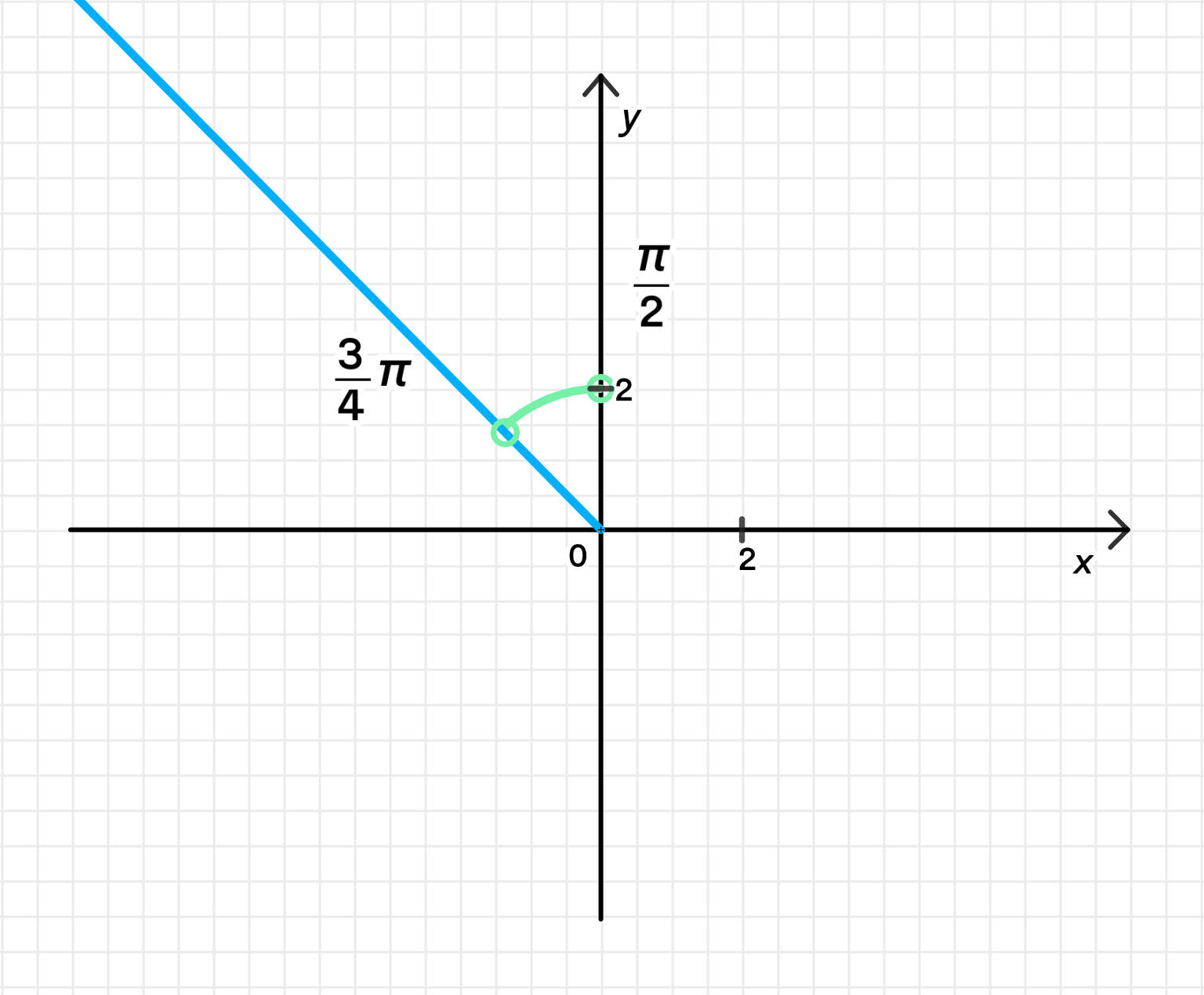
а)

Нам дано условие:

$$\frac{\pi}{2} < \arg(z) < \frac{3\pi}{4} \quad \text{и} \quad |z| = 2;$$ $$90^\circ < a < 135^\circ \quad \text{и} \quad R = 2;$$

Пояснение:

Угол аргумента $\arg(z)$: Условие $\frac{\pi}{2} < \arg(z) < \frac{3\pi}{4}$ ограничивает угол $a$ от $90^\circ$ до $135^\circ$, что соответствует сектору, который лежит в второй четверти комплексной плоскости. Это область, где вещественная часть числа отрицательна, а мнимая положительна.

Модуль $|z|$: Условие $|z| = 2$ говорит о том, что все числа должны находиться на окружности радиусом 2, которая имеет центр в начале координат. Таким образом, мы ограничены только кругом радиуса 2, и все числа $z$ должны лежать на этой окружности.

Рисунок:

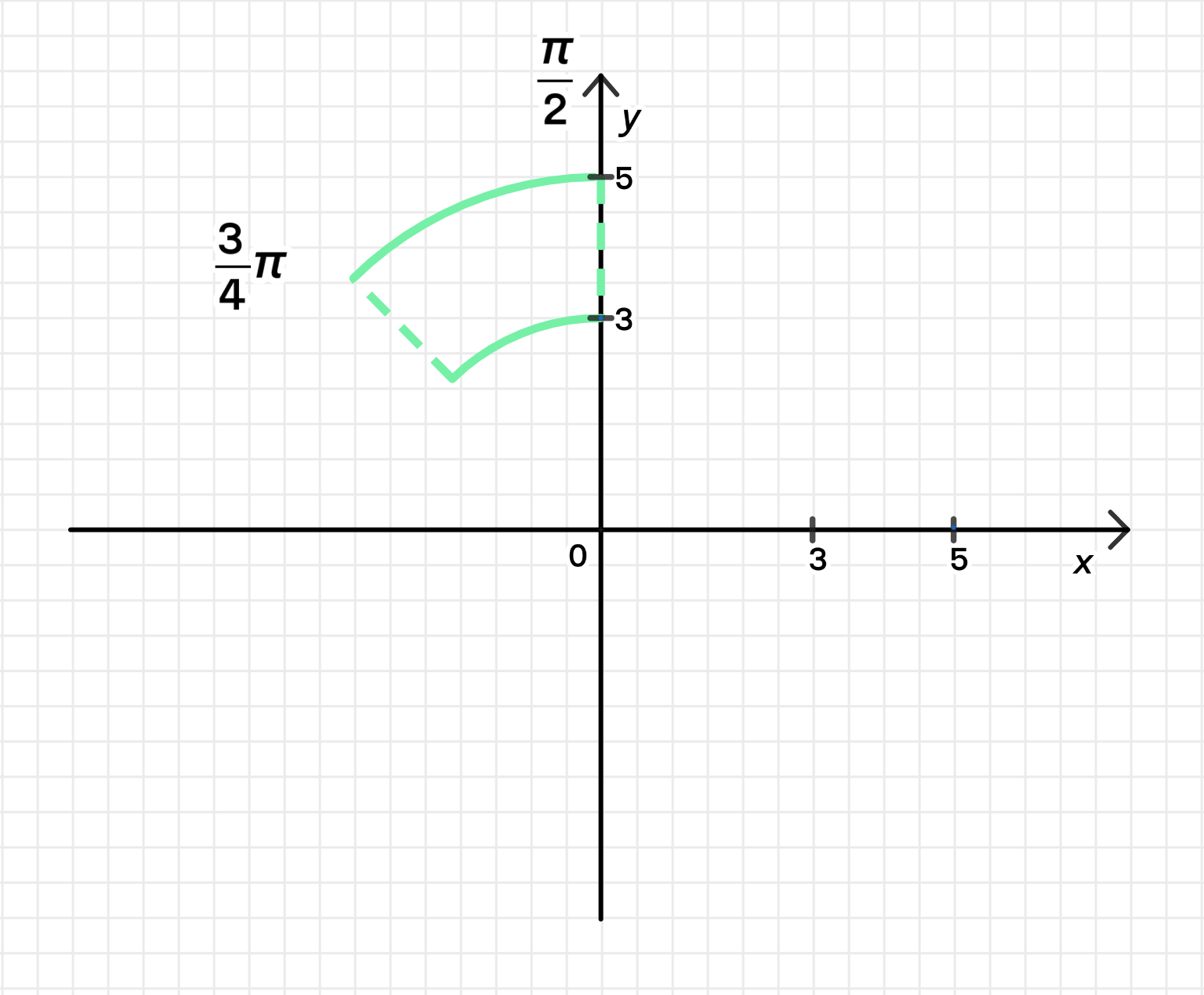
б)

Нам дано условие:

$$\frac{\pi}{2} < \arg(z) < \frac{3\pi}{4} \quad \text{и} \quad 3 < |z| < 5;$$ $$90^\circ < a < 135^\circ \quad \text{и} \quad 3 < R < 5;$$

Пояснение:

Угол аргумента $\arg(z)$: Как и в предыдущем случае, угол $a$ находится в пределах от $90^\circ$ до $135^\circ$, что также ограничивает сектор во второй четверти.

Модуль $|z|$: Условие $3 < |z| < 5$ означает, что числа должны лежать в кольце между двумя окружностями: одной радиусом 3 и другой радиусом 5. Мы рассматриваем только те числа, которые находятся в этом кольце.

Рисунок:

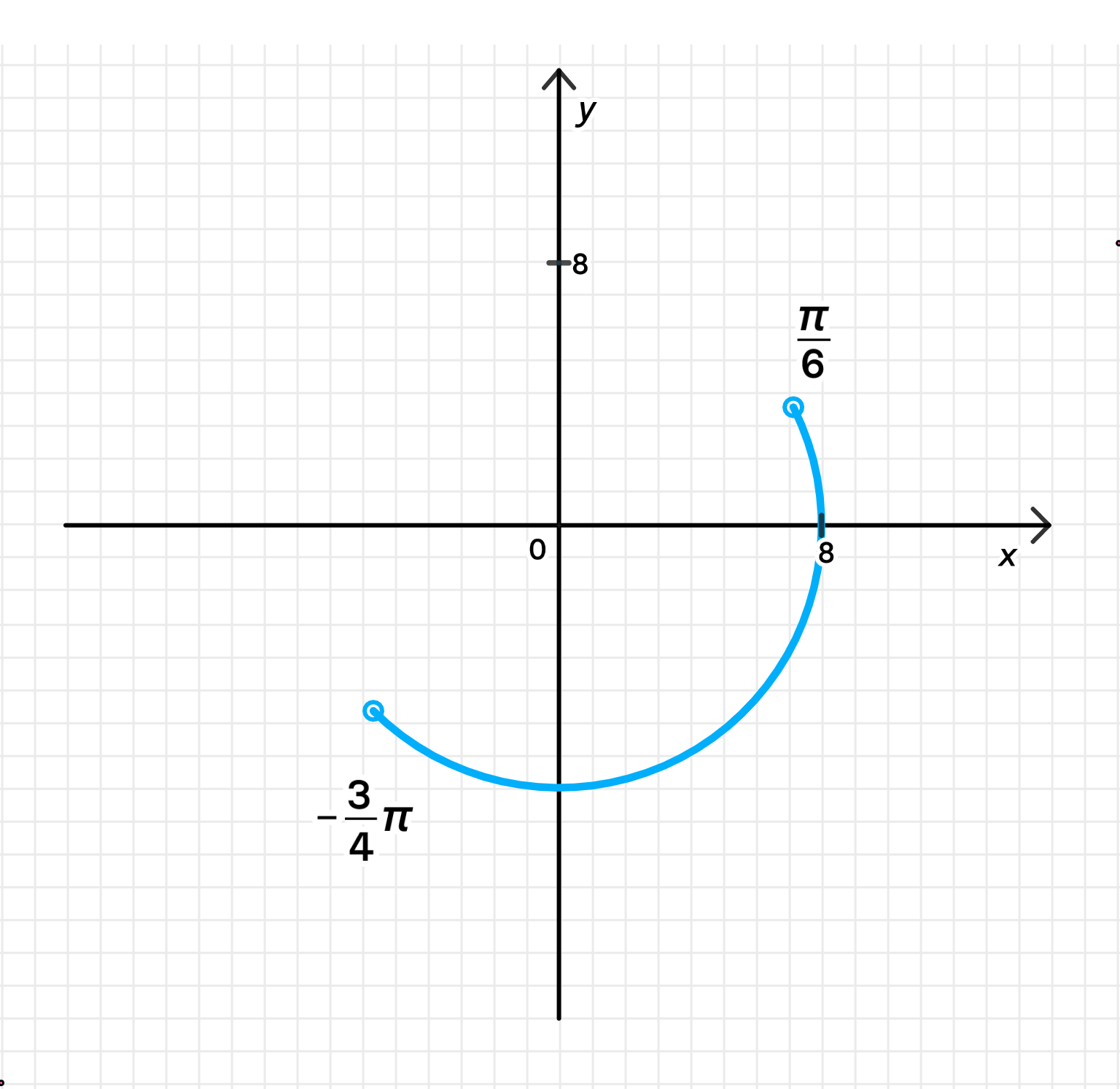
в)

Нам дано условие:

$$-\frac{3\pi}{4} < \arg(z) < \frac{\pi}{6} \quad \text{и} \quad |z| = 8;$$ $$-135^\circ < a < 30^\circ \quad \text{и} \quad R = 8;$$

Пояснение:

Угол аргумента $\arg(z)$: Условие $-\frac{3\pi}{4} < \arg(z) < \frac{\pi}{6}$ ограничивает угол $a$ от $-135^\circ$ до $30^\circ$. Это значит, что все числа находятся в четвертой и первой четвертях комплексной плоскости, то есть вещественная часть чисел положительна или отрицательна, а мнимая часть может быть как положительной, так и отрицательной.

Модуль $|z|$: Условие $|z| = 8$ говорит о том, что все числа находятся на окружности радиусом 8, которая имеет центр в начале координат.

Рисунок:

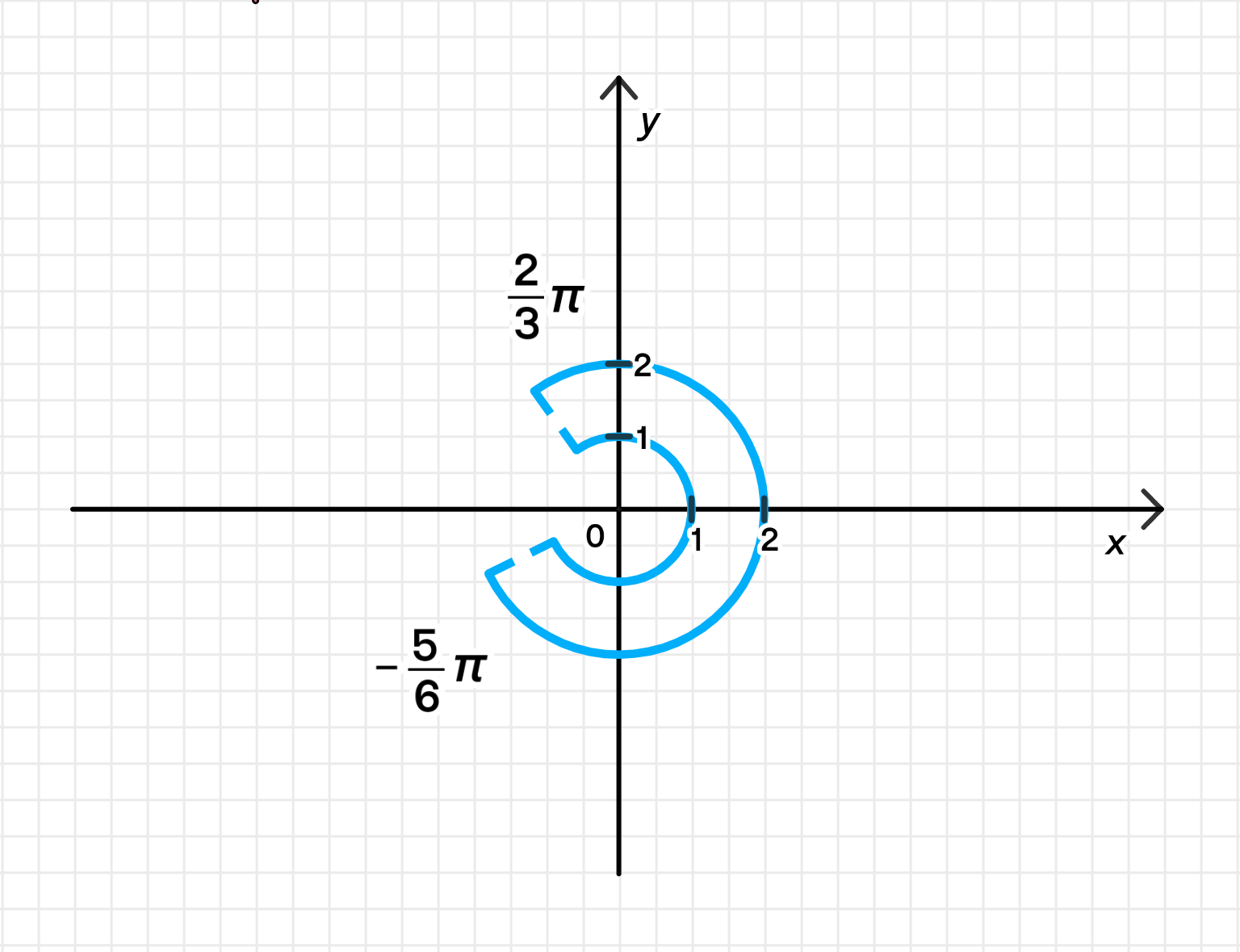
г)

Нам дано условие:

$$-\frac{5\pi}{6} < \arg(z) < \frac{2\pi}{3} \quad \text{или} \quad 1 < |z| < 2;$$ $$-150^\circ < a < 120^\circ \quad \text{или} \quad 1 < R < 2;$$

Пояснение:

Угол аргумента $\arg(z)$: Условие $-\frac{5\pi}{6} < \arg(z) < \frac{2\pi}{3}$ указывает на два диапазона углов:

• от $-150^\circ$ до $120^\circ$, что охватывает области второй, третьей и четвертой четвертей.

Кроме того, второе условие $1 < |z| < 2$ предполагает, что значения модуля чисел $z$ находятся в кольце между окружностями радиусов 1 и 2.

Модуль $|z|$: Условие $1 < R < 2$ говорит о том, что числа $z$ лежат в кольце радиусами 1 и 2.

Рисунок: