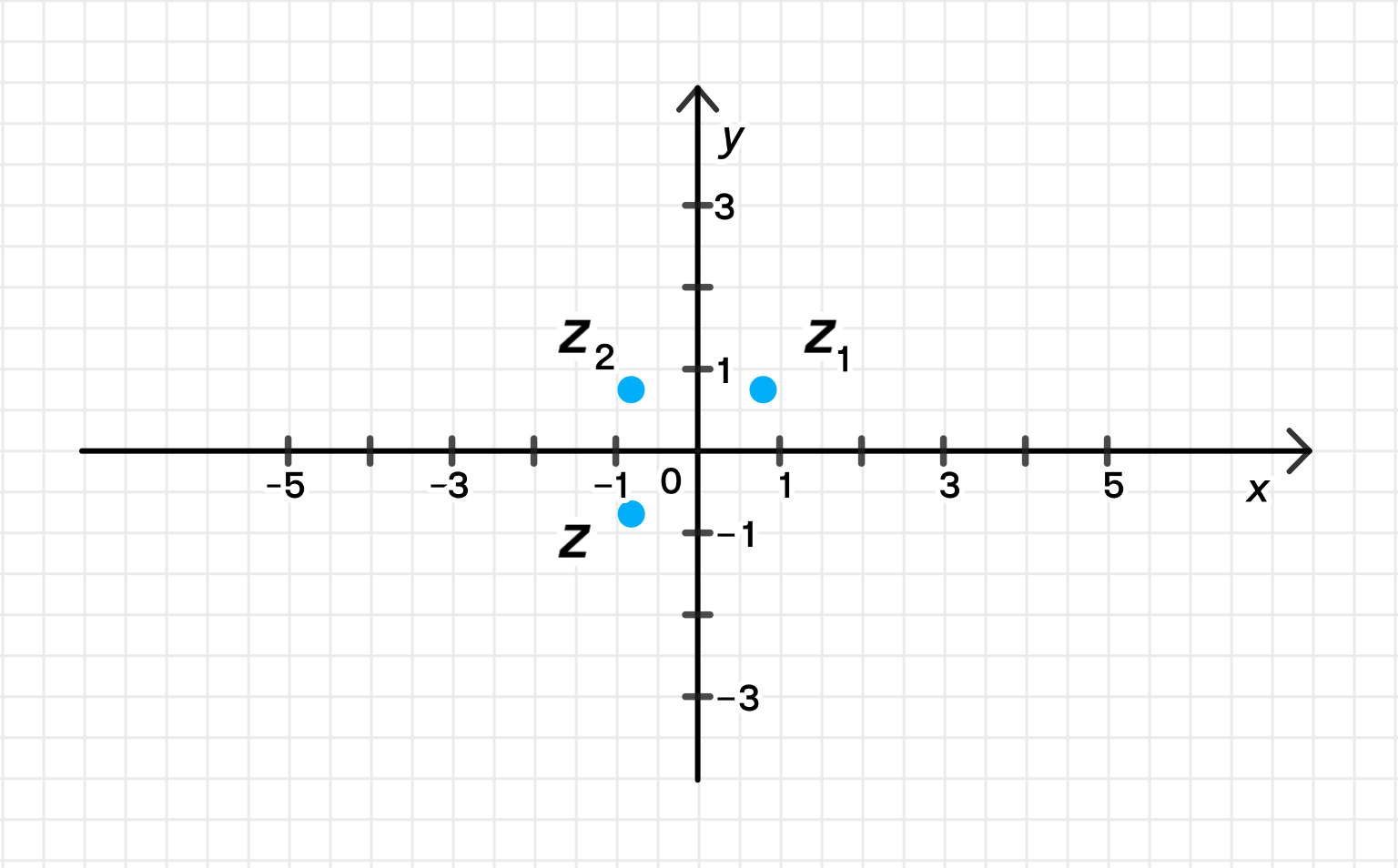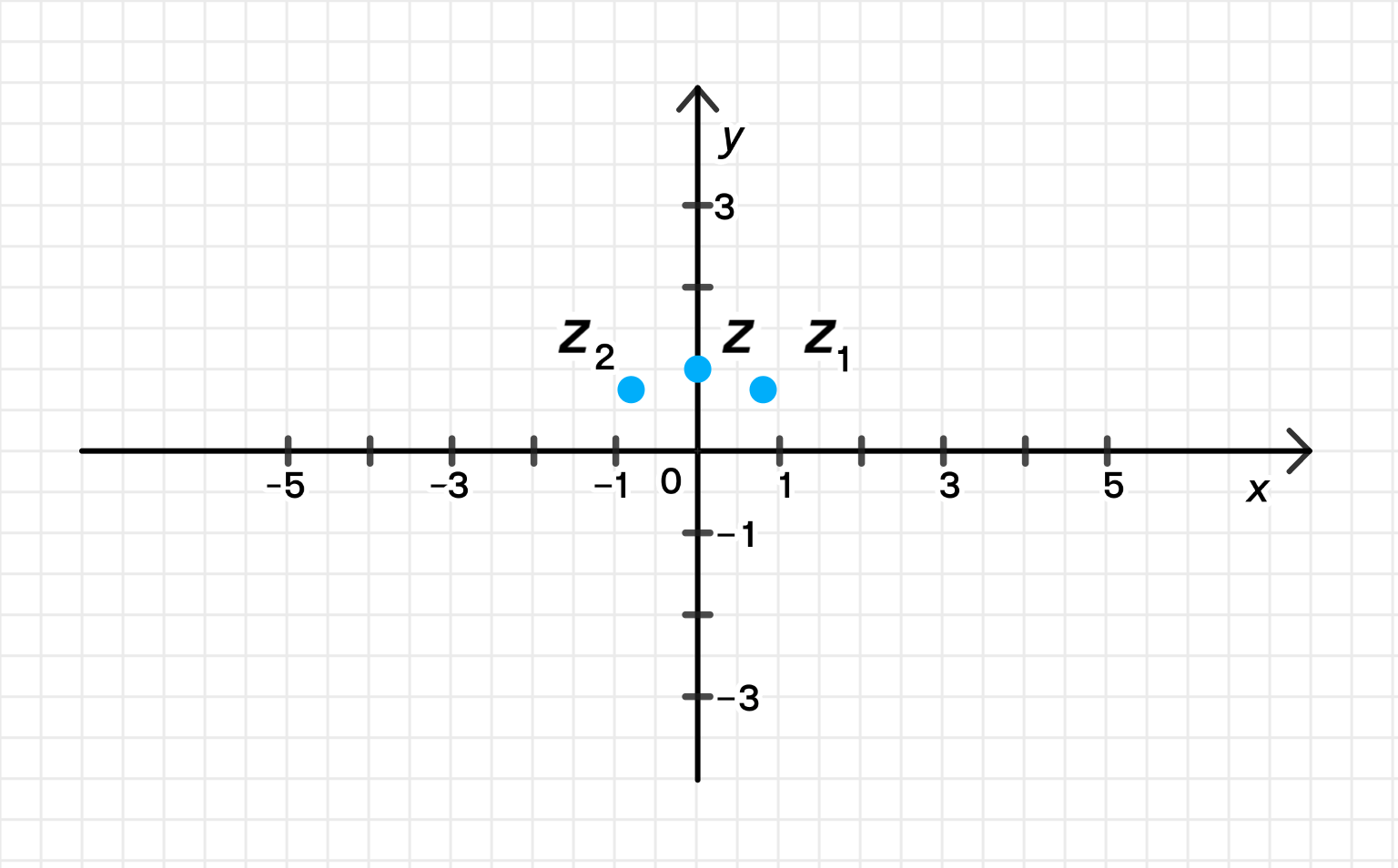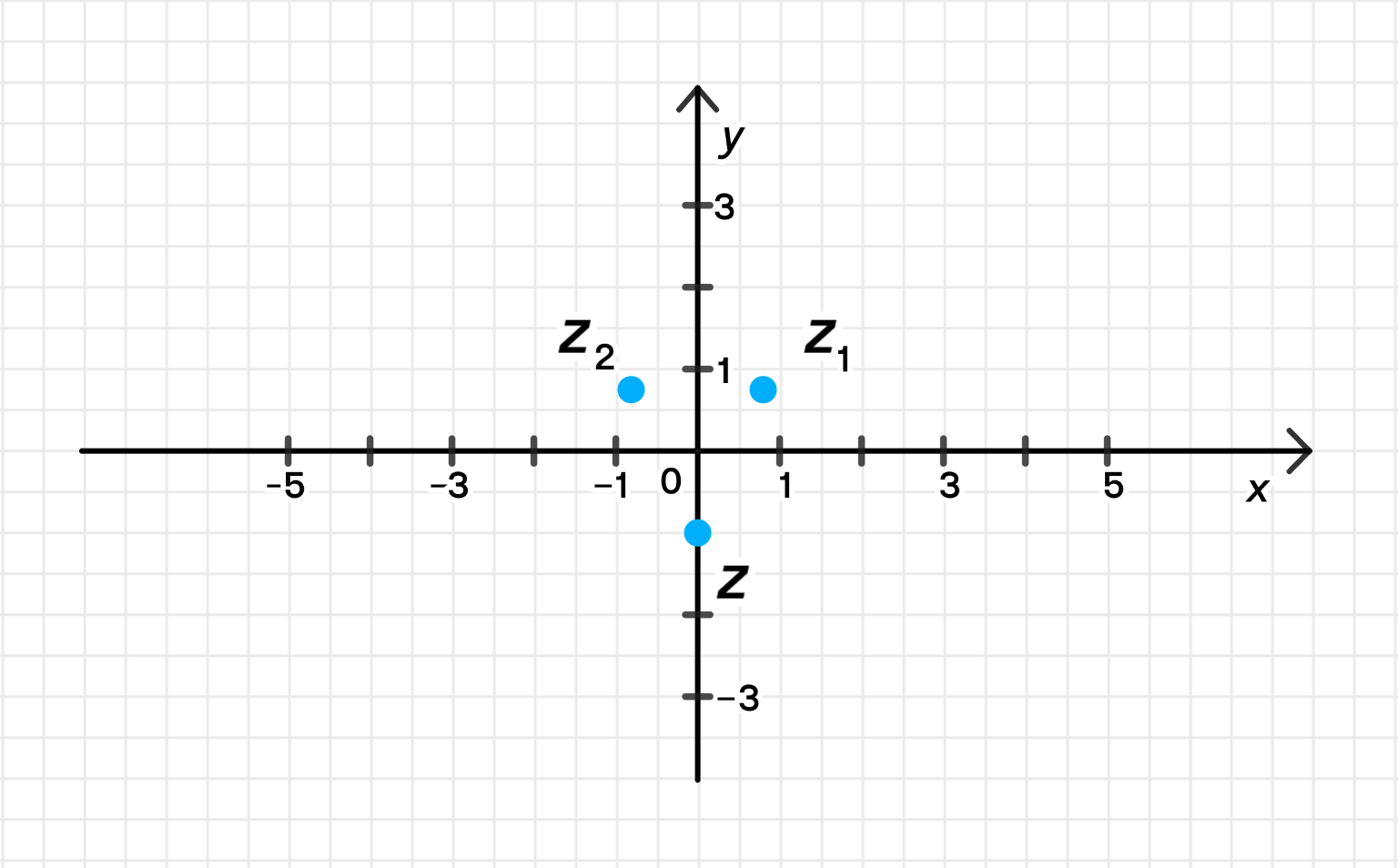ГДЗ по Алгебре 10 Класс Номер 34.33 Профильный Уровень Мордкович — Подробные Ответы

Даны комплексные числа:

$$z_1 = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4};$$ $$z_2 = -\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i = \cos \frac{3\pi}{4} + i \sin \frac{3\pi}{4};$$

а) $z = z_1 z_2 = 1 \cdot 1 \cdot \left( \cos \left( \frac{\pi}{4} + \frac{3\pi}{4} \right) + i \sin \left( \frac{\pi}{4} + \frac{3\pi}{4} \right) \right);$

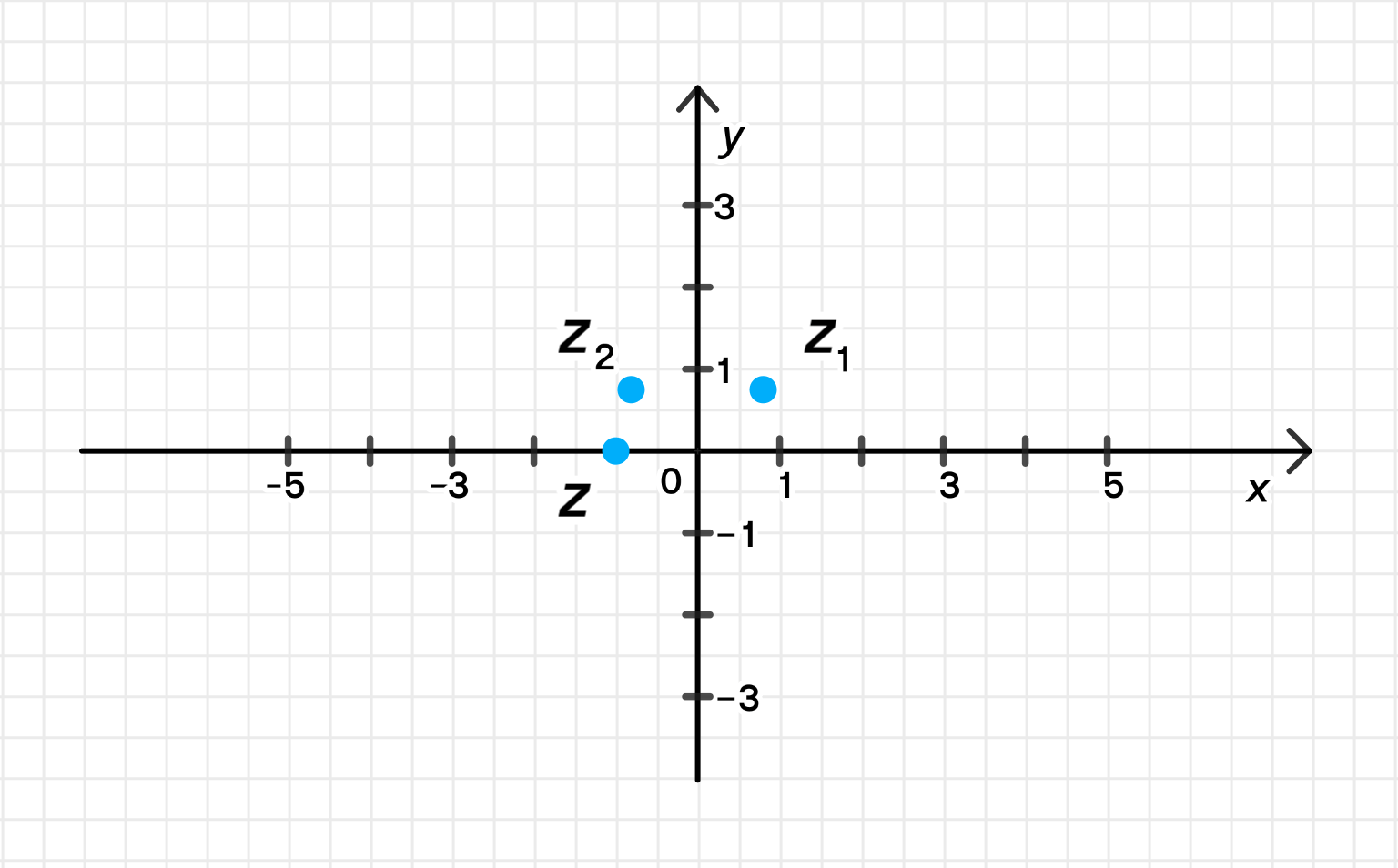
$$z = \cos \frac{4\pi}{4} + i \sin \frac{4\pi}{4} = \cos \pi + i \sin \pi = -1 + i \cdot 0 = -1;$$

Данные числа на комплексной плоскости:

Ответ: $\arg z = \pi$.

б) $z = (z_1)^2 z_2 = 1^2 \cdot 1 \cdot \left( \cos \left( \frac{2\pi}{4} + \frac{3\pi}{4} \right) + i \sin \left( \frac{2\pi}{4} + \frac{3\pi}{4} \right) \right);$

$$z = \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4} = \cos \left( -\frac{3\pi}{4} \right) + i \sin \left( -\frac{3\pi}{4} \right);$$

Данные числа на комплексной плоскости:

Ответ: $\arg z = -\frac{3\pi}{4}$.

в) $z = z_1 (z_2)^3 = 1 \cdot 1^3 \cdot \left( \cos \left( \frac{\pi}{4} + 3 \cdot \frac{3\pi}{4} \right) + i \sin \left( \frac{\pi}{4} + 3 \cdot \frac{3\pi}{4} \right) \right);$

$$z = \cos \frac{10\pi}{4} + i \sin \frac{10\pi}{4} = \cos \frac{5\pi}{2} + i \sin \frac{5\pi}{2} = \cos \frac{\pi}{2} + i \sin \frac{\pi}{2};$$ $$z = 0 + i \cdot 1 = i;$$

Данные числа на комплексной плоскости:

Ответ: $\arg z = \frac{\pi}{2}$.

г) $z = (z_1)^5 (z_2)^3 = 1^5 \cdot 1^3 \cdot \left( \cos \left( \frac{5\pi}{4} + 3 \cdot \frac{3\pi}{4} \right) + i \sin \left( \frac{5\pi}{4} + 3 \cdot \frac{3\pi}{4} \right) \right);$

$$z = \cos \frac{14\pi}{4} + i \sin \frac{14\pi}{4} = \cos \frac{7\pi}{2} + i \sin \frac{7\pi}{2} = \cos \left( -\frac{\pi}{2} \right) + i \sin \left( -\frac{\pi}{2} \right);$$ $$z = \cos \frac{\pi}{2} — i \sin \frac{\pi}{2} = 0 — i \cdot 1 = -i;$$

Данные числа на комплексной плоскости:

Ответ: $\arg z = -\frac{\pi}{2}$.

Дано:

• $z_1 = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4}$
• $z_2 = -\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i = \cos \frac{3\pi}{4} + i \sin \frac{3\pi}{4}$

Эти комплексные числа записаны в тригонометрической форме.

а) $z = z_1 z_2$

1. Умножение комплексных чисел в тригонометрической форме:

Для умножения двух комплексных чисел в тригонометрической форме $z_1 = r_1 (\cos \theta_1 + i \sin \theta_1)$ и $z_2 = r_2 (\cos \theta_2 + i \sin \theta_2)$, используется формула:

$$z = r_1 r_2 \left( \cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2) \right)$$

где $r_1$ и $r_2$ — модули чисел, а $\theta_1$ и $\theta_2$ — их аргументы.

2. Для $z_1$ и $z_2$:

• Модуль $|z_1| = 1$, так как $\left( \frac{\sqrt{2}}{2} \right)^2 + \left( \frac{\sqrt{2}}{2} \right)^2 = 1$.
• Модуль $|z_2| = 1$, так как $\left( -\frac{\sqrt{2}}{2} \right)^2 + \left( \frac{\sqrt{2}}{2} \right)^2 = 1$.
• Аргумент $\arg(z_1) = \frac{\pi}{4}$.
• Аргумент $\arg(z_2) = \frac{3\pi}{4}$.

Теперь применим формулу умножения:

$$z = 1 \cdot 1 \left( \cos \left( \frac{\pi}{4} + \frac{3\pi}{4} \right) + i \sin \left( \frac{\pi}{4} + \frac{3\pi}{4} \right) \right)$$ $$z = \cos \pi + i \sin \pi = -1 + i \cdot 0 = -1$$

Ответ: $z = -1$.

Графическое представление на комплексной плоскости:

б) $z = (z_1)^2 z_2$

1. Для вычисления $z_1^2$:

Для возведения комплексного числа в степень $n$ в тригонометрической форме используется формула:

$$z^n = r^n \left( \cos(n\theta) + i \sin(n\theta) \right)$$

где $r$ — модуль числа, а $\theta$ — его аргумент.

Для $z_1$, мы возводим в квадрат:

$$z_1^2 = 1^2 \left( \cos \left( 2 \cdot \frac{\pi}{4} \right) + i \sin \left( 2 \cdot \frac{\pi}{4} \right) \right)$$ $$z_1^2 = \cos \frac{\pi}{2} + i \sin \frac{\pi}{2}$$

Теперь умножим на $z_2$:

$$z = z_1^2 z_2 = 1 \cdot 1 \left( \cos \left( \frac{\pi}{2} + \frac{3\pi}{4} \right) + i \sin \left( \frac{\pi}{2} + \frac{3\pi}{4} \right) \right)$$ $$z = \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4}$$

Аргумент этого числа:

$$\arg(z) = \frac{5\pi}{4} = -\frac{3\pi}{4} \quad (\text{потому что } \frac{5\pi}{4} = -\frac{3\pi}{4} \text{ по модулю } 2\pi)$$

Ответ: $z = \cos \left( -\frac{3\pi}{4} \right) + i \sin \left( -\frac{3\pi}{4} \right)$.

Графическое представление на комплексной плоскости:

в) $z = z_1 (z_2)^3$

1. Для вычисления $z_2^3$:

Используем ту же формулу для возведения в степень:

$$z_2^3 = 1^3 \left( \cos \left( 3 \cdot \frac{3\pi}{4} \right) + i \sin \left( 3 \cdot \frac{3\pi}{4} \right) \right)$$ $$z_2^3 = \cos \frac{9\pi}{4} + i \sin \frac{9\pi}{4}$$

Так как $\frac{9\pi}{4} = 2\pi + \frac{\pi}{4}$, то:

$$z_2^3 = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4}$$

Теперь умножим на $z_1$:

$$z = z_1 z_2^3 = 1 \cdot 1 \left( \cos \left( \frac{\pi}{4} + \frac{\pi}{4} \right) + i \sin \left( \frac{\pi}{4} + \frac{\pi}{4} \right) \right)$$ $$z = \cos \frac{2\pi}{4} + i \sin \frac{2\pi}{4} = \cos \frac{\pi}{2} + i \sin \frac{\pi}{2}$$ $$z = 0 + i \cdot 1 = i$$

Ответ: $z = i$.

Графическое представление на комплексной плоскости:

г) $z=(z_1{)}^5(z_2{)}^3$

1. Для вычисления $z_1^5$:

Используем формулу для возведения в степень:

$$z_1^5 = 1^5 \left( \cos \left( 5 \cdot \frac{\pi}{4} \right) + i \sin \left( 5 \cdot \frac{\pi}{4} \right) \right)$$ $$z_1^5 = \cos \frac{5\pi}{4} + i \sin \frac{5\pi}{4}$$

Теперь вычислим $z_2^3$:

$$z_2^3 = 1^3 \left( \cos \left( 3 \cdot \frac{3\pi}{4} \right) + i \sin \left( 3 \cdot \frac{3\pi}{4} \right) \right)$$ $$z_2^3 = \cos \frac{9\pi}{4} + i \sin \frac{9\pi}{4} = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4}$$

Теперь умножим $z_1^5$ и $z_2^3$:

$$z = z_1^5 z_2^3 = 1 \cdot 1 \left( \cos \left( \frac{5\pi}{4} + \frac{\pi}{4} \right) + i \sin \left( \frac{5\pi}{4} + \frac{\pi}{4} \right) \right)$$ $$z = \cos \frac{6\pi}{4} + i \sin \frac{6\pi}{4} = \cos \frac{3\pi}{2} + i \sin \frac{3\pi}{2}$$ $$z = 0 — i = -i$$

Ответ: $z = -i$.

Графическое представление на комплексной плоскости:

Итоги:

а) $z = -1$, $\arg(z) = \pi$

б) $z = \cos \left( -\frac{3\pi}{4} \right) + i \sin \left( -\frac{3\pi}{4} \right)$, $\arg(z) = -\frac{3\pi}{4}$

в) $z = i$, $\arg(z) = \frac{\pi}{2}$

г) $z = -i$, $\arg(z) = -\frac{\pi}{2}$