ГДЗ по Алгебре 10 Класс Номер 34.34 Профильный Уровень Мордкович — Подробные Ответы

Даны комплексные числа:

$$z_1 = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i = \cos\frac{\pi}{4} + i\sin\frac{\pi}{4};$$ $$z_2 = -\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i = \cos\frac{3\pi}{4} + i\sin\frac{3\pi}{4}.$$

а)

$$z = \frac{z_1}{z_2} = \frac{1}{1} \cdot \left( \cos\left(\frac{\pi}{4} — \frac{3\pi}{4}\right) + i\sin\left(\frac{\pi}{4} — \frac{3\pi}{4}\right) \right);$$ $$z = \cos\left(-\frac{2\pi}{4}\right) + i\sin\left(-\frac{2\pi}{4}\right) = \cos\left(-\frac{\pi}{2}\right) + i\sin\left(-\frac{\pi}{2}\right);$$ $$z = \cos\frac{\pi}{2} — i\sin\frac{\pi}{2} = 0 — i \cdot 1 = -i.$$

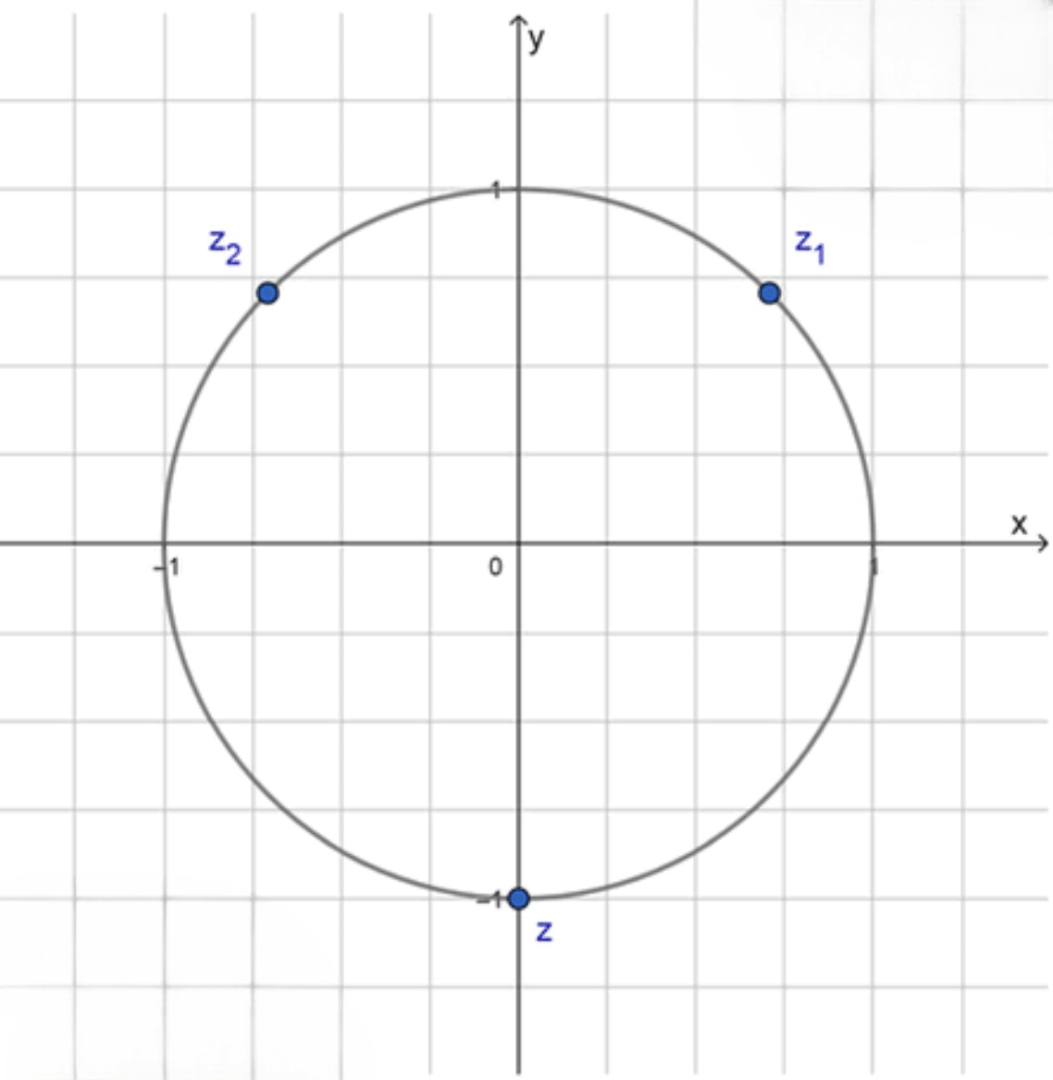
Данные числа на комплексной плоскости:

Ответ: $\arg z = -\frac{\pi}{2}$.

б)

$$z = \frac{z_2}{z_1} = \frac{1}{1} \cdot \left( \cos\left(\frac{3\pi}{4} — \frac{\pi}{4}\right) + i\sin\left(\frac{3\pi}{4} — \frac{\pi}{4}\right) \right);$$ $$z = \cos\frac{2\pi}{4} + i\sin\frac{2\pi}{4} = \cos\frac{\pi}{2} + i\sin\frac{\pi}{2};$$ $$z = \cos\frac{\pi}{2} + i\sin\frac{\pi}{2} = 0 + i \cdot 1 = i.$$

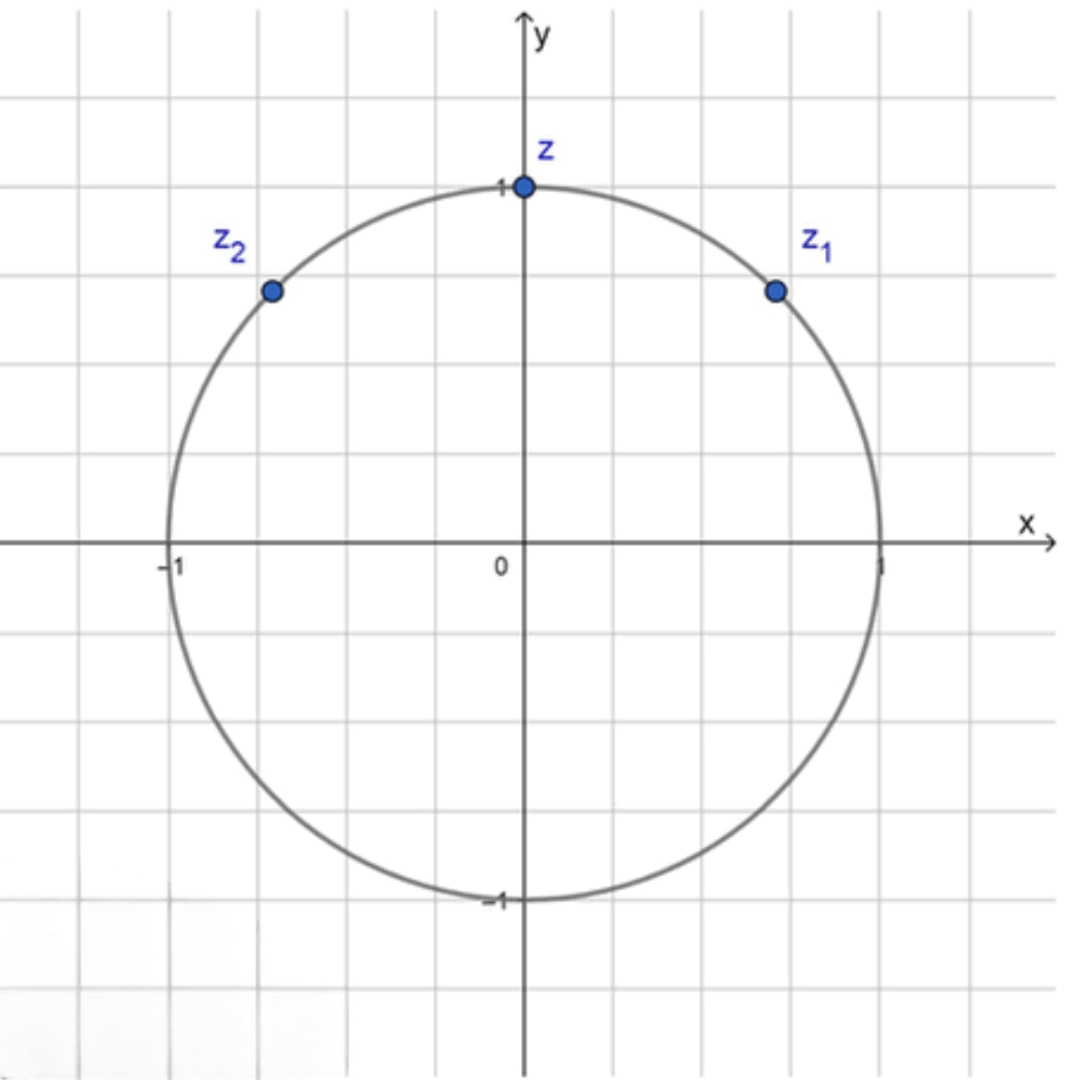
Данные числа на комплексной плоскости:

Ответ: $\arg z = \frac{\pi}{2}$.

в)

$$z = \frac{z_1^2}{z_2} = \frac{1^2}{1} \cdot \left( \cos\left(\frac{2\pi}{4} — \frac{3\pi}{4}\right) + i\sin\left(\frac{2\pi}{4} — \frac{3\pi}{4}\right) \right);$$ $$z = \cos\left(-\frac{\pi}{4}\right) + i\sin\left(-\frac{\pi}{4}\right).$$

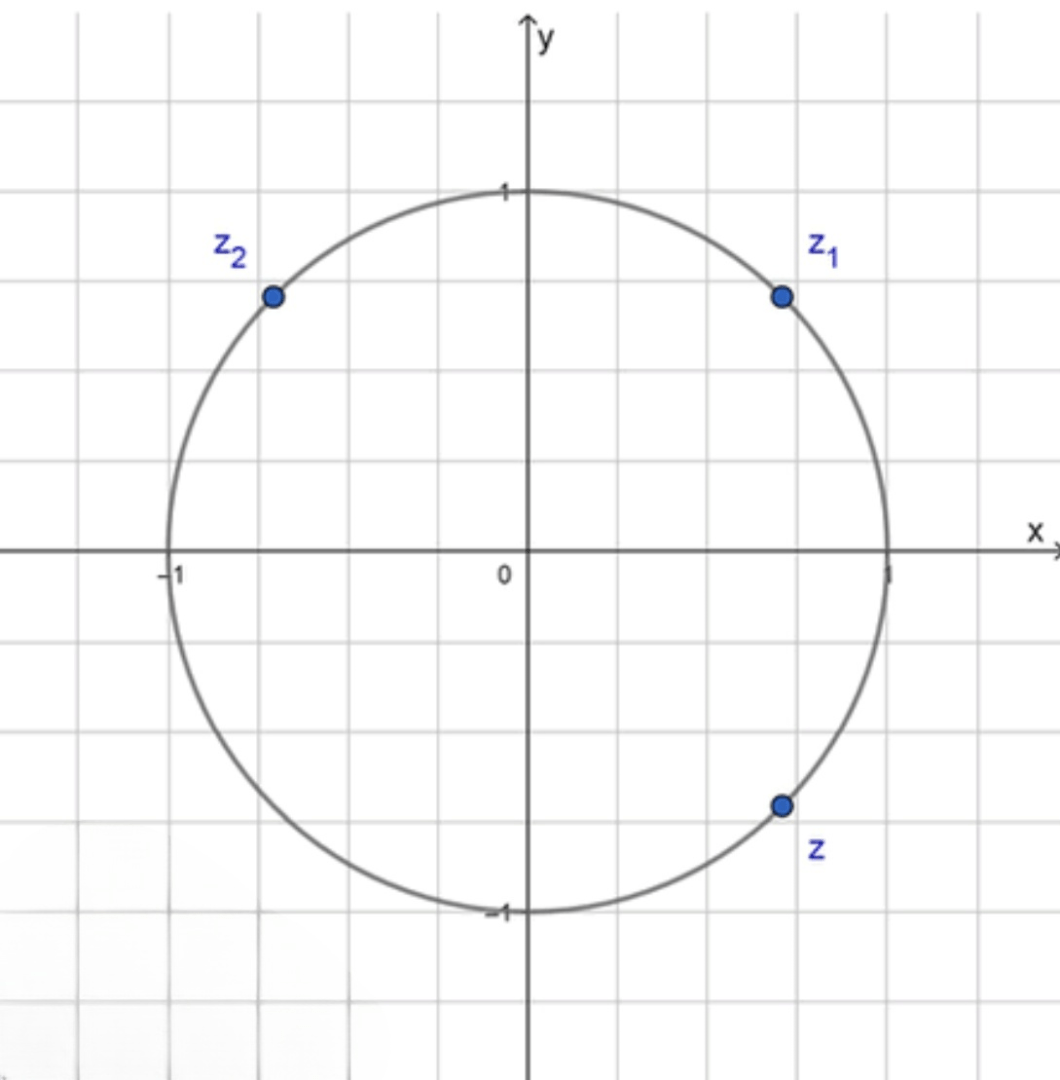
Данные числа на комплексной плоскости:

Ответ: $\arg z = -\frac{\pi}{4}$.

г)

$$z = \frac{z_1^3}{z_2^5} = \frac{1^3}{1^5} \cdot \left( \cos\left(\frac{3\pi}{4} — 5 \cdot \frac{3\pi}{4}\right) + i\sin\left(\frac{3\pi}{4} — 5 \cdot \frac{3\pi}{4}\right) \right);$$ $$z = \cos\left(-\frac{12\pi}{4}\right) + i\sin\left(-\frac{12\pi}{4}\right) = \cos(-3\pi) + i\sin(-3\pi);$$ $$z = \cos\pi + i\sin\pi = -1 + i \cdot 0 = -1.$$

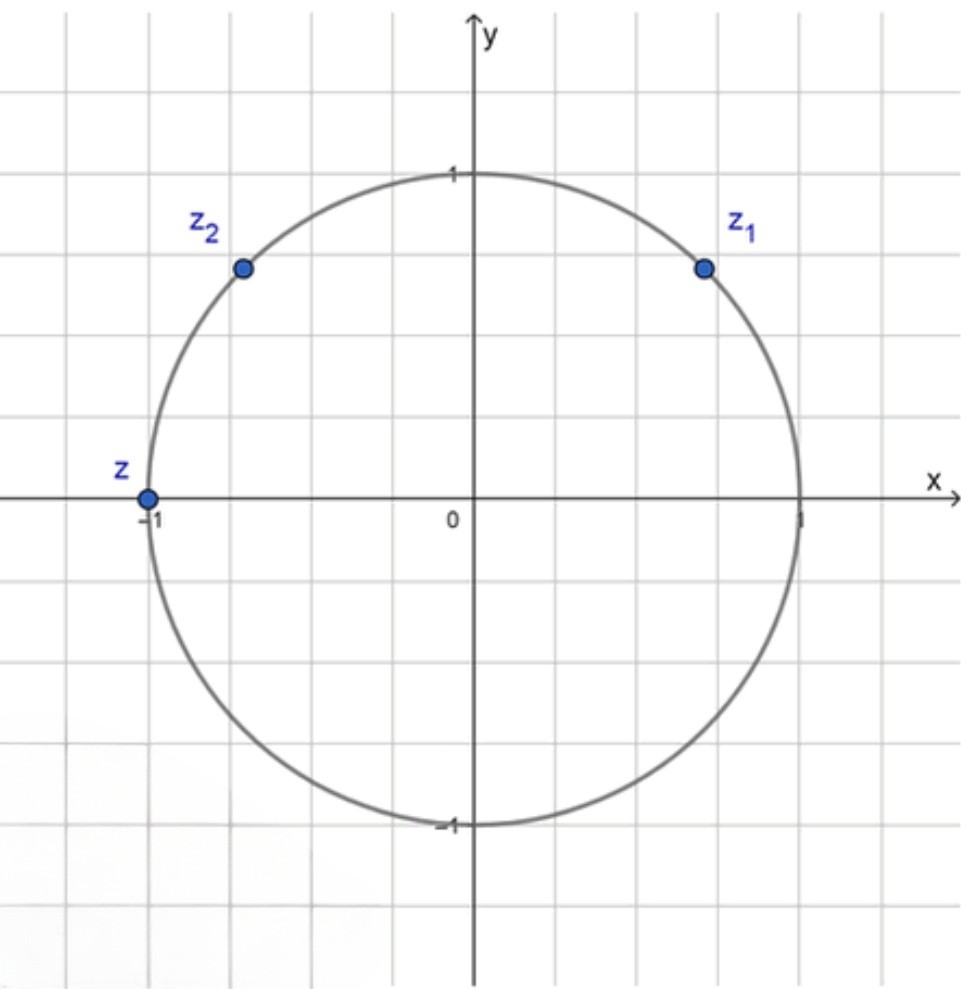
Данные числа на комплексной плоскости:

Ответ: $\arg z = \pi$.

Даны два комплексных числа:

$$z_1 = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4}$$ $$z_2 = -\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}i = \cos \frac{3\pi}{4} + i \sin \frac{3\pi}{4}$$

Комплексные числа уже приведены к тригонометрической форме. Рассмотрим каждый из пунктов задачи.

а) $z = \frac{z_1}{z_2}$

1. Применяем формулу для деления комплексных чисел в тригонометрической форме:

Для двух комплексных чисел в тригонометрической форме $z_1 = r_1 \left( \cos \theta_1 + i \sin \theta_1 \right)$ и $z_2 = r_2 \left( \cos \theta_2 + i \sin \theta_2 \right)$ формула для их деления выглядит так:

$$\frac{z_1}{z_2} = \frac{r_1}{r_2} \left( \cos (\theta_1 — \theta_2) + i \sin (\theta_1 — \theta_2) \right)$$

где $r_1$ и $r_2$ — модули чисел $z_1$ и $z_2$, а $\theta_1$ и $\theta_2$ — их аргументы.

2. Модуль и аргумент числа $z_1$:

• Модуль $|z_1| = \sqrt{\left( \frac{\sqrt{2}}{2} \right)^2 + \left( \frac{\sqrt{2}}{2} \right)^2} = \sqrt{\frac{2}{2}} = 1$.
• Аргумент $\arg(z_1) = \frac{\pi}{4}$.

3. Модуль и аргумент числа $z_2$:

• Модуль $|z_2| = \sqrt{\left( -\frac{\sqrt{2}}{2} \right)^2 + \left( \frac{\sqrt{2}}{2} \right)^2} = 1$.
• Аргумент $\arg(z_2) = \frac{3\pi}{4}$.

4. Вычисляем $z$:

$$z = \frac{z_1}{z_2} = \frac{1}{1} \left( \cos \left( \frac{\pi}{4} — \frac{3\pi}{4} \right) + i \sin \left( \frac{\pi}{4} — \frac{3\pi}{4} \right) \right)$$ $$z = \cos \left( -\frac{2\pi}{4} \right) + i \sin \left( -\frac{2\pi}{4} \right) = \cos \left( -\frac{\pi}{2} \right) + i \sin \left( -\frac{\pi}{2} \right)$$ $$z = 0 — i \cdot 1 = -i$$

Ответ: $z = -i$.

Аргумент числа: $\arg(z) = -\frac{\pi}{2}$.

Графическое представление на комплексной плоскости:

б) $z = \frac{z_2}{z_1}$

1. Применяем ту же формулу для деления:

$$z = \frac{z_2}{z_1} = \frac{1}{1} \left( \cos \left( \frac{3\pi}{4} — \frac{\pi}{4} \right) + i \sin \left( \frac{3\pi}{4} — \frac{\pi}{4} \right) \right)$$ $$z = \cos \frac{2\pi}{4} + i \sin \frac{2\pi}{4} = \cos \frac{\pi}{2} + i \sin \frac{\pi}{2}$$ $$z = 0 + i \cdot 1 = i$$

Ответ: $z = i$.

Аргумент числа: $\arg(z) = \frac{\pi}{2}$.

Графическое представление на комплексной плоскости:

в) $z = \frac{z_1^2}{z_2}$

1. Сначала возводим $z_1$ в квадрат. Используем формулу для возведения числа в степень:

$$z_1^2 = r_1^2 \left( \cos (2\theta_1) + i \sin (2\theta_1) \right)$$

Поскольку $r_1 = 1$ и $\theta_1 = \frac{\pi}{4}$, получаем:

$$z_1^2 = 1^2 \left( \cos \left( 2 \cdot \frac{\pi}{4} \right) + i \sin \left( 2 \cdot \frac{\pi}{4} \right) \right) = \cos \frac{\pi}{2} + i \sin \frac{\pi}{2}$$ $$z_1^2 = 0 + i \cdot 1 = i$$

2. Теперь делим $z_1^2$ на $z_2$:

$$z = \frac{z_1^2}{z_2} = \frac{1}{1} \left( \cos \left( \frac{\pi}{2} — \frac{3\pi}{4} \right) + i \sin \left( \frac{\pi}{2} — \frac{3\pi}{4} \right) \right)$$ $$z = \cos \left( -\frac{\pi}{4} \right) + i \sin \left( -\frac{\pi}{4} \right)$$

Ответ: $z = \cos \left( -\frac{\pi}{4} \right) + i \sin \left( -\frac{\pi}{4} \right)$.

Аргумент числа: $\arg(z) = -\frac{\pi}{4}$.

Графическое представление на комплексной плоскости:

г) $z = \frac{z_1^3}{z_2^5}$

1. Сначала возводим $z_1$ в куб, используя формулу для возведения в степень:

$$z_1^3 = r_1^3 \left( \cos (3\theta_1) + i \sin (3\theta_1) \right)$$

Поскольку $r_1 = 1$ и $\theta_1 = \frac{\pi}{4}$, получаем:

$$z_1^3 = 1^3 \left( \cos \left( 3 \cdot \frac{\pi}{4} \right) + i \sin \left( 3 \cdot \frac{\pi}{4} \right) \right) = \cos \frac{3\pi}{4} + i \sin \frac{3\pi}{4}$$

2. Возводим $z_2$ в пятую степень:

$$z_2^5 = r_2^5 \left( \cos (5\theta_2) + i \sin (5\theta_2) \right)$$

Поскольку $r_2 = 1$ и $\theta_2 = \frac{3\pi}{4}$, получаем:

$$z_2^5 = 1^5 \left( \cos \left( 5 \cdot \frac{3\pi}{4} \right) + i \sin \left( 5 \cdot \frac{3\pi}{4} \right) \right) = \cos \frac{15\pi}{4} + i \sin \frac{15\pi}{4}$$

Так как $\frac{15\pi}{4} = 2\pi + \frac{7\pi}{4}$, то:

$$z_2^5 = \cos \frac{7\pi}{4} + i \sin \frac{7\pi}{4} = \cos \left( -\frac{\pi}{4} \right) + i \sin \left( -\frac{\pi}{4} \right)$$

3. Теперь делим $z_1^3$ на $z_2^5$:

$$z = \frac{z_1^3}{z_2^5} = \frac{1}{1} \left( \cos \left( \frac{3\pi}{4} — \left( -\frac{\pi}{4} \right) \right) + i \sin \left( \frac{3\pi}{4} — \left( -\frac{\pi}{4} \right) \right) \right)$$ $$z = \cos \left( \frac{3\pi}{4} + \frac{\pi}{4} \right) + i \sin \left( \frac{3\pi}{4} + \frac{\pi}{4} \right) = \cos \pi + i \sin \pi$$ $$z = -1 + 0i = -1$$

Ответ: $z = -1$.

Аргумент числа: $\arg(z) = \pi$.

Графическое представление на комплексной плоскости:

Итоги:

а) $z = -i$, $\arg(z) = -\frac{\pi}{2}$

б) $z = i$, $\arg(z) = \frac{\pi}{2}$

в) $z = \cos \left( -\frac{\pi}{4} \right) + i \sin \left( -\frac{\pi}{4} \right)$, $\arg(z) = -\frac{\pi}{4}$

г) $z = -1$, $\arg(z) = \pi$