ГДЗ по Алгебре 10 Класс Номер 34.35 Профильный Уровень Мордкович — Подробные Ответы

Даны комплексные числа:

$$z_1 = \frac{1}{2} + \frac{\sqrt{3}}{2}i = \cos \frac{\pi}{3} + i \sin \frac{\pi}{3};$$ $$z_2 = -\frac{\sqrt{3}}{2} + \frac{1}{2}i = \cos \frac{5\pi}{6} + i \sin \frac{5\pi}{6};$$

a) $z = z_1 z_2$:

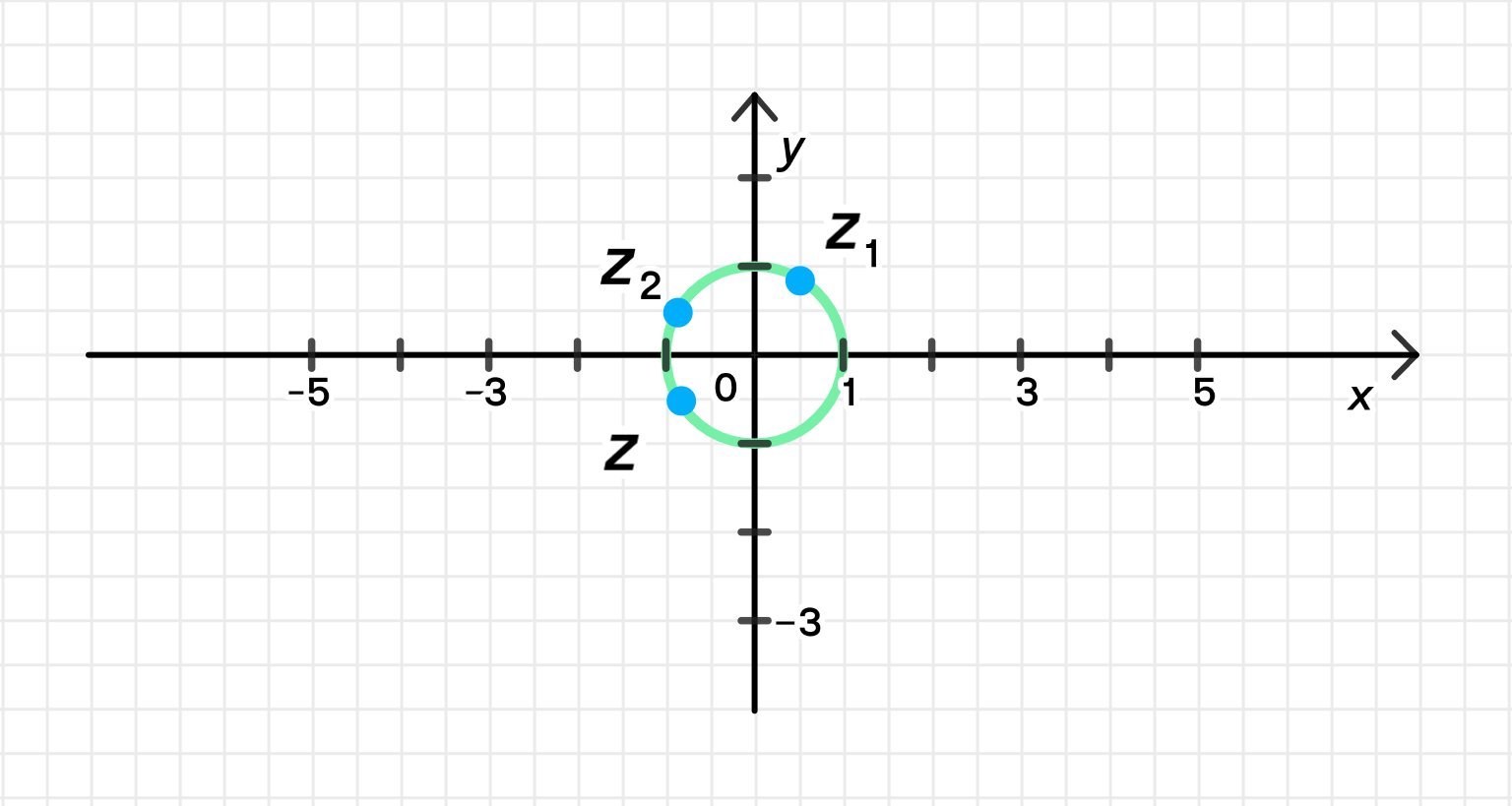
$$z = z_1 z_2 = 1 \cdot 1 \cdot \left( \cos \left( \frac{\pi}{3} + \frac{5\pi}{6} \right) + i \sin \left( \frac{\pi}{3} + \frac{5\pi}{6} \right) \right);$$ $$z = \cos \frac{7\pi}{6} + i \sin \frac{7\pi}{6} = \cos \left( -\frac{5\pi}{6} \right) + i \sin \left( -\frac{5\pi}{6} \right);$$

Данные числа на комплексной плоскости:

Ответ: $\arg z = -\frac{5\pi}{6}$.

б) $z = (z_1)^2 z_2$:

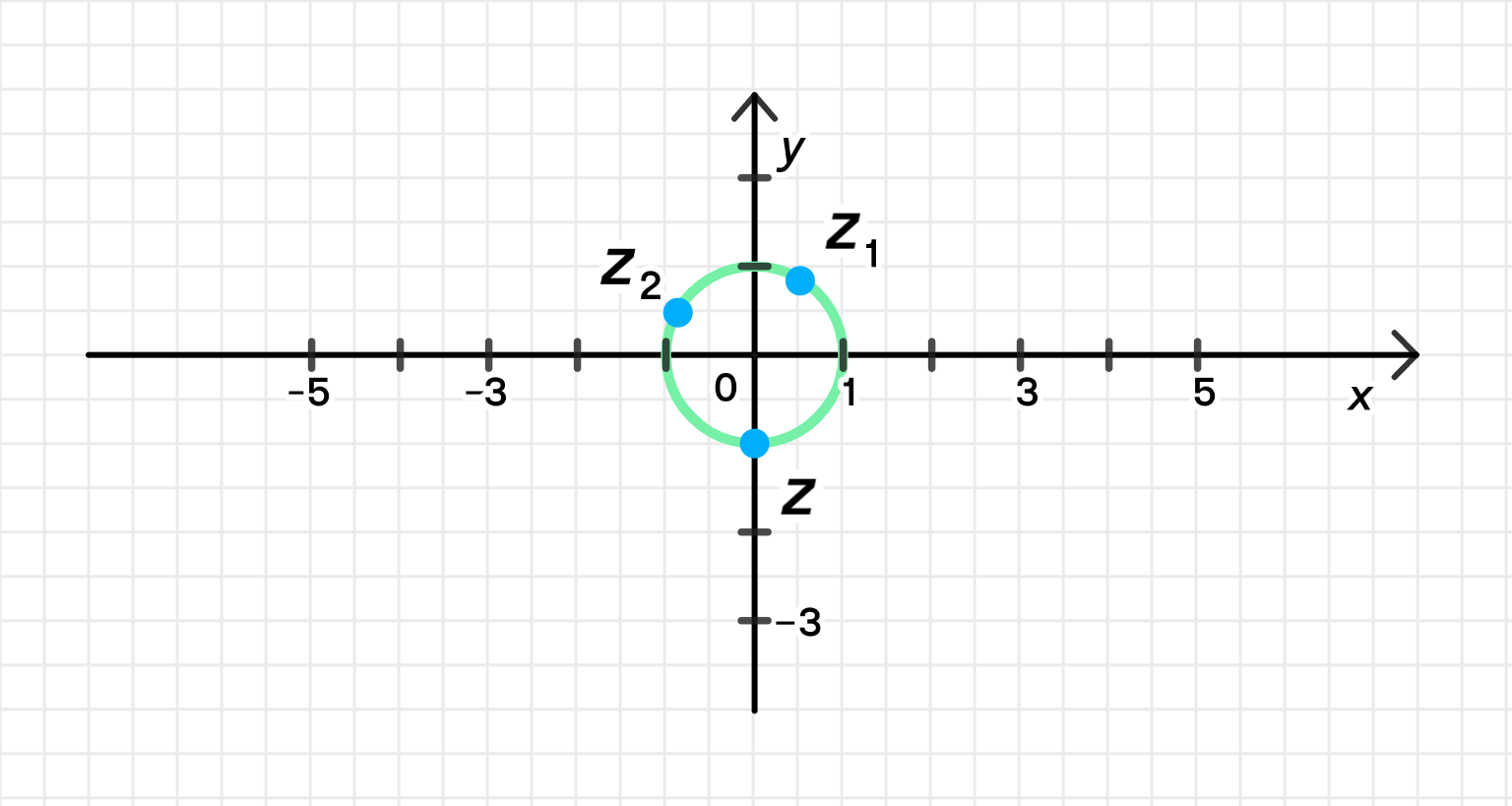
$$z = (z_1)^2 z_2 = 1^2 \cdot 1 \cdot \left( \cos \left( \frac{2\pi}{3} + \frac{5\pi}{6} \right) + i \sin \left( \frac{2\pi}{3} + \frac{5\pi}{6} \right) \right);$$ $$z = \cos \frac{9\pi}{6} + i \sin \frac{9\pi}{6} = \cos \frac{3\pi}{2} + i \sin \frac{3\pi}{2} = \cos \left( -\frac{\pi}{2} \right) + i \sin \left( -\frac{\pi}{2} \right);$$ $$z = \cos \frac{\pi}{2} — i \sin \frac{\pi}{2} = 0 — i \cdot 1 = -i;$$

Данные числа на комплексной плоскости:

Ответ: $\arg z = -\frac{\pi}{2}$.

в) $z = z_1 (z_2)^5$:

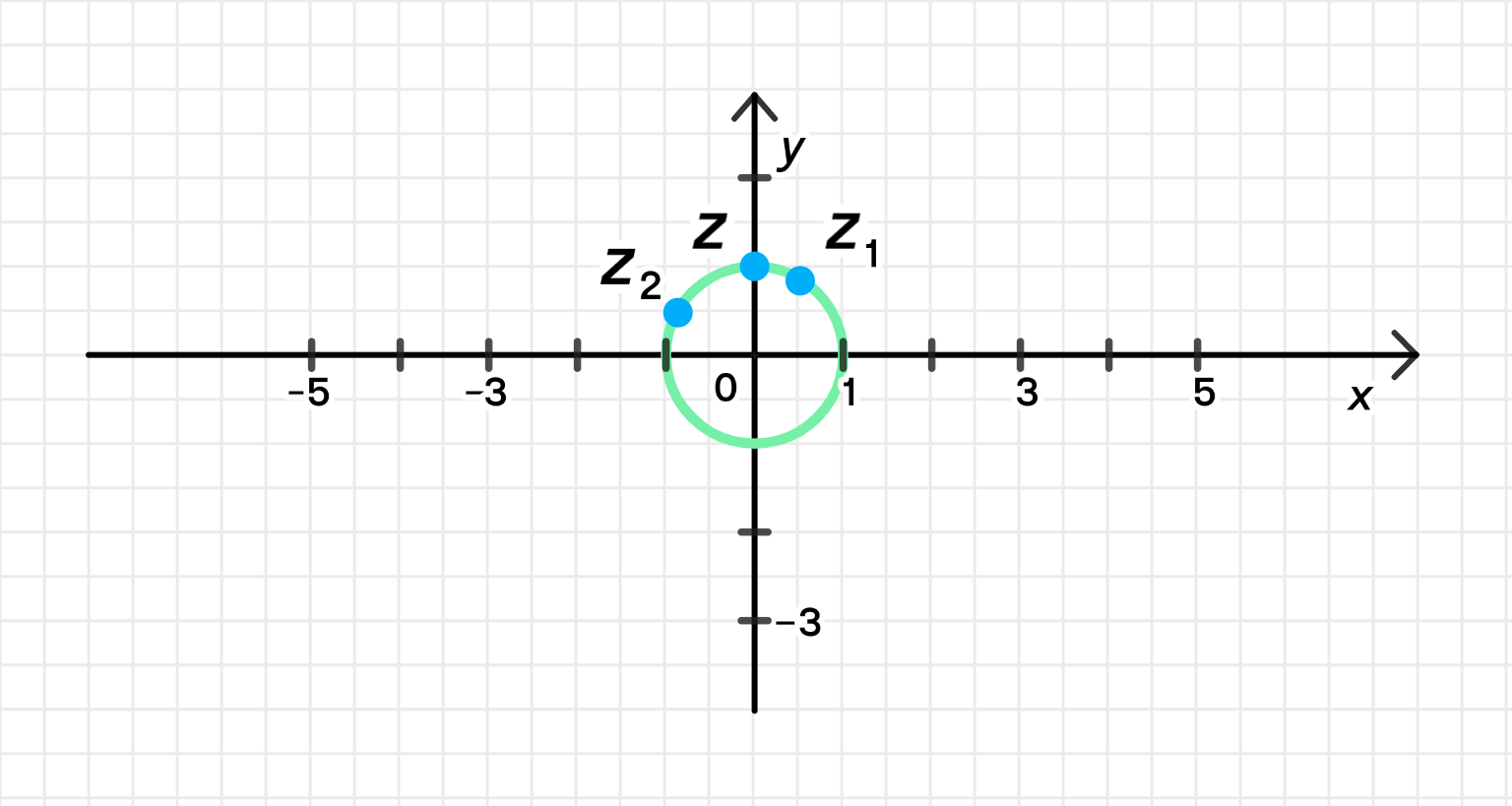
$$z = z_1 (z_2)^5 = 1 \cdot 1^5 \cdot \left( \cos \left( \frac{\pi}{3} + \frac{5 \cdot 5\pi}{6} \right) + i \sin \left( \frac{\pi}{3} + \frac{5 \cdot 5\pi}{6} \right) \right);$$ $$z = \cos \frac{27\pi}{6} + i \sin \frac{27\pi}{6} = \cos \frac{3\pi}{6} + i \sin \frac{3\pi}{6} = \cos \frac{\pi}{2} + i \sin \frac{\pi}{2};$$ $$z = 0 + i \cdot 1 = i;$$

Данные числа на комплексной плоскости:

Ответ: $\arg z = \frac{\pi}{2}$.

г) $z = (z_1)^{11} (z_2)^{10}$:

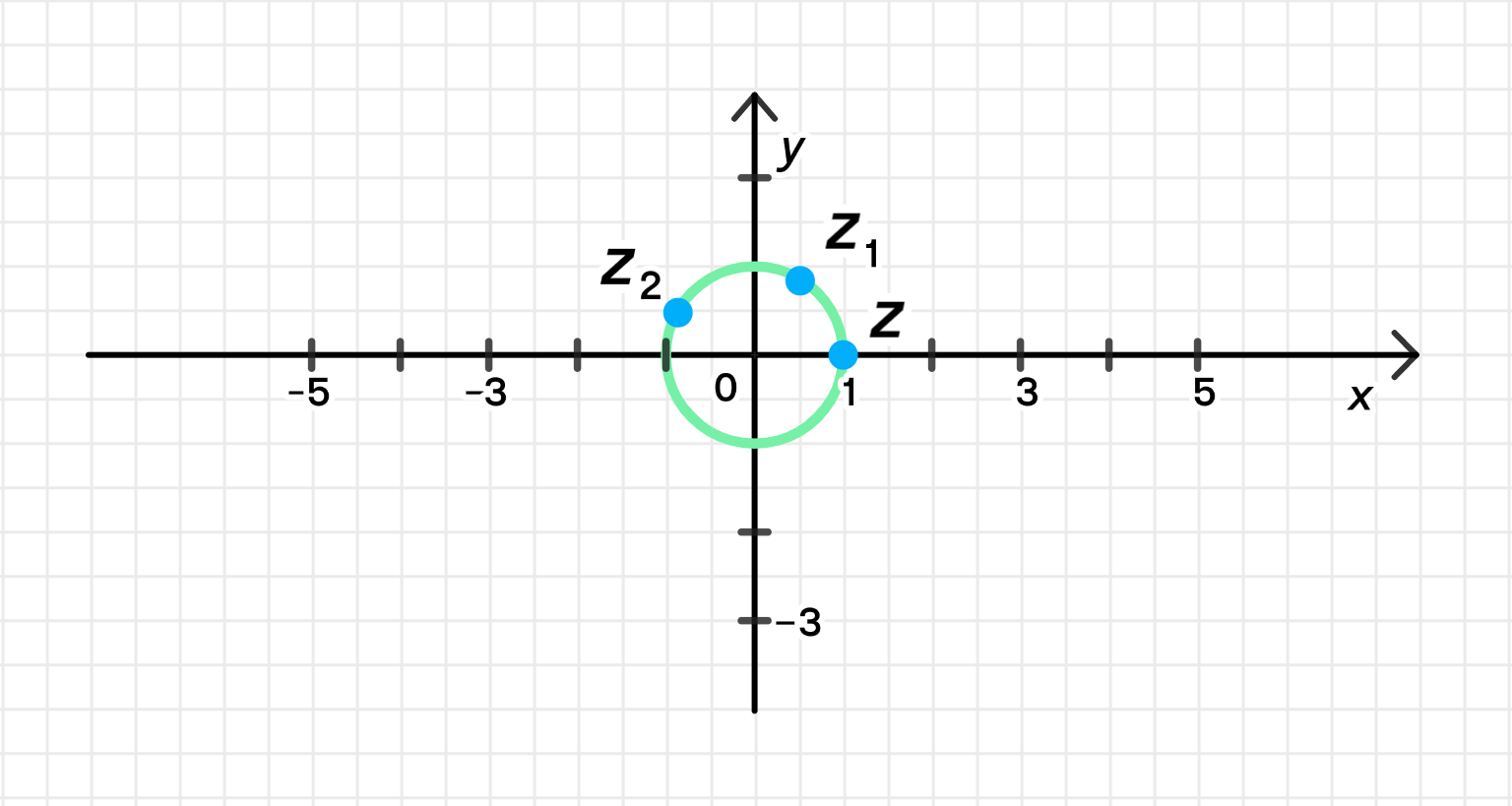
$$z = (z_1)^{11} (z_2)^{10} = 1^{11} \cdot 1^{10} \cdot \left( \cos \left( \frac{11\pi}{3} + \frac{50\pi}{6} \right) + i \sin \left( \frac{11\pi}{3} + \frac{50\pi}{6} \right) \right);$$ $$z = \cos \frac{72\pi}{6} + i \sin \frac{72\pi}{6} = \cos 12\pi + i \sin 12\pi = \cos 0 + i \sin 0;$$ $$z = 1 + i \cdot 0 = 1;$$

Данные числа на комплексной плоскости:

Ответ: $\arg z = 0$.

Даны два комплексных числа в тригонометрической форме:

$$z_1 = \frac{1}{2} + \frac{\sqrt{3}}{2}i = \cos \frac{\pi}{3} + i \sin \frac{\pi}{3},$$ $$z_2 = -\frac{\sqrt{3}}{2} + \frac{1}{2}i = \cos \frac{5\pi}{6} + i \sin \frac{5\pi}{6}.$$

Комплексное число $z_1$ имеет модуль 1 и аргумент $\frac{\pi}{3}$, а комплексное число $z_2$ также имеет модуль 1 и аргумент $\frac{5\pi}{6}$.

а) $z = z_1 z_2$

Нам нужно найти произведение двух комплексных чисел. В тригонометрической форме произведение $z_1 z_2$ можно выразить как:

$$z = z_1 z_2 = |z_1| |z_2| \left( \cos(\arg z_1 + \arg z_2) + i \sin(\arg z_1 + \arg z_2) \right),$$

где $|z_1|$ и $|z_2|$ — это модуль комплексных чисел $z_1$ и $z_2$, а $\arg z_1$ и $\arg z_2$ — это их аргументы.

Модули чисел: $|z_1| = 1$ и $|z_2| = 1$.

Аргументы чисел: $\arg z_1 = \frac{\pi}{3}$ и $\arg z_2 = \frac{5\pi}{6}$.

Теперь вычислим аргумент произведения:

$$\arg z = \arg z_1 + \arg z_2 = \frac{\pi}{3} + \frac{5\pi}{6} = \frac{2\pi}{6} + \frac{5\pi}{6} = \frac{7\pi}{6}.$$

Таким образом, $z$ имеет форму:

$$z = 1 \cdot 1 \left( \cos \frac{7\pi}{6} + i \sin \frac{7\pi}{6} \right) = \cos \frac{7\pi}{6} + i \sin \frac{7\pi}{6}.$$

Также можно записать это через тригонометрическую форму угла:

$$\cos \frac{7\pi}{6} = \cos \left( -\frac{5\pi}{6} \right), \quad \sin \frac{7\pi}{6} = \sin \left( -\frac{5\pi}{6} \right),$$

поскольку $\frac{7\pi}{6} = -\frac{5\pi}{6} + 2\pi$.

Итак, получаем:

$$z = \cos \left( -\frac{5\pi}{6} \right) + i \sin \left( -\frac{5\pi}{6} \right).$$

Ответ: $\arg z = -\frac{5\pi}{6}$.

б) $z = (z_1)^2 z_2$

Нам нужно вычислить выражение $(z_1)^2 z_2$. Для этого используем формулы для возведения комплексного числа в степень и для произведения комплексных чисел.

Сначала возведем $z_1$ в квадрат:

$$z_1^2 = |z_1|^2 \left( \cos(2 \cdot \arg z_1) + i \sin(2 \cdot \arg z_1) \right).$$

Поскольку $|z_1| = 1$, то $|z_1^2| = 1$, и получаем:

$$z_1^2 = \cos \left( 2 \cdot \frac{\pi}{3} \right) + i \sin \left( 2 \cdot \frac{\pi}{3} \right) = \cos \frac{2\pi}{3} + i \sin \frac{2\pi}{3}.$$

Теперь умножим $z_1^2$ на $z_2$. Для этого используем аналогичную формулу для произведения:

$$z = z_1^2 z_2 = |z_1^2| |z_2| \left( \cos \left( \arg z_1^2 + \arg z_2 \right) + i \sin \left( \arg z_1^2 + \arg z_2 \right) \right).$$

Поскольку $|z_1^2| = 1$ и $|z_2| = 1$, получаем:

$$z = \cos \left( \frac{2\pi}{3} + \frac{5\pi}{6} \right) + i \sin \left( \frac{2\pi}{3} + \frac{5\pi}{6} \right).$$

Выполнив сложение углов:

$$\frac{2\pi}{3} + \frac{5\pi}{6} = \frac{4\pi}{6} + \frac{5\pi}{6} = \frac{9\pi}{6} = \frac{3\pi}{2}.$$

Итак, $z = \cos \frac{3\pi}{2} + i \sin \frac{3\pi}{2}$, что можно записать как:

$$z = \cos \left( -\frac{\pi}{2} \right) + i \sin \left( -\frac{\pi}{2} \right).$$

Таким образом:

$$z = \cos \frac{\pi}{2} — i \sin \frac{\pi}{2} = -i.$$

Ответ: $\arg z = -\frac{\pi}{2}$.

в) $z = z_1 (z_2)^5$

Теперь вычислим выражение $z_1 (z_2)^5$. Используем аналогичный подход:

Возведем $z_2$ в пятую степень:

$$z_2^5 = |z_2|^5 \left( \cos \left( 5 \cdot \arg z_2 \right) + i \sin \left( 5 \cdot \arg z_2 \right) \right).$$

Поскольку $|z_2| = 1$, то $|z_2^5| = 1$, и получаем:

$$z_2^5 = \cos \left( 5 \cdot \frac{5\pi}{6} \right) + i \sin \left( 5 \cdot \frac{5\pi}{6} \right) = \cos \frac{25\pi}{6} + i \sin \frac{25\pi}{6}.$$

Преобразуем угол:

$$\frac{25\pi}{6} = 4\pi + \frac{\pi}{6} \quad \Rightarrow \quad \cos \frac{25\pi}{6} = \cos \frac{\pi}{6}, \quad \sin \frac{25\pi}{6} = \sin \frac{\pi}{6}.$$

Таким образом:

$$z_2^5 = \cos \frac{\pi}{6} + i \sin \frac{\pi}{6}.$$

Теперь умножим $z_1$ на $z_2^5$:

$$z = z_1 z_2^5 = 1 \cdot 1 \left( \cos \left( \frac{\pi}{3} + \frac{\pi}{6} \right) + i \sin \left( \frac{\pi}{3} + \frac{\pi}{6} \right) \right).$$

Выполнив сложение углов:

$$\frac{\pi}{3} + \frac{\pi}{6} = \frac{2\pi}{6} + \frac{\pi}{6} = \frac{3\pi}{6} = \frac{\pi}{2}.$$

Таким образом:

$$z = \cos \frac{\pi}{2} + i \sin \frac{\pi}{2}.$$

Это число на комплексной плоскости представляет собой $i$.

Ответ: $\arg z = \frac{\pi}{2}$.

г) $z = (z_1)^{11} (z_2)^{10}$

Для последней части задачи:

Возведем $z_1$ в 11-ю степень:

$$z_1^{11} = |z_1|^{11} \left( \cos \left( 11 \cdot \arg z_1 \right) + i \sin \left( 11 \cdot \arg z_1 \right) \right).$$

Поскольку $|z_1| = 1$, получаем:

$$z_1^{11} = \cos \left( 11 \cdot \frac{\pi}{3} \right) + i \sin \left( 11 \cdot \frac{\pi}{3} \right).$$

Вычислим угол:

$$11 \cdot \frac{\pi}{3} = \frac{11\pi}{3} = 2\pi + \frac{5\pi}{3},$$

и угловой стандарт:

$$\frac{5\pi}{3} = -\frac{\pi}{3}.$$

Таким образом:

$$z_1^{11} = \cos \left( -\frac{\pi}{3} \right) + i \sin \left( -\frac{\pi}{3} \right).$$

Возведем $z_2$ в 10-ю степень:

$$z_2^{10} = |z_2|^{10} \left( \cos \left( 10 \cdot \arg z_2 \right) + i \sin \left( 10 \cdot \arg z_2 \right) \right).$$

Поскольку $|z_2| = 1$, получаем:

$$z_2^{10} = \cos \left( 10 \cdot \frac{5\pi}{6} \right) + i \sin \left( 10 \cdot \frac{5\pi}{6} \right).$$

Вычислим угол:

$$10 \cdot \frac{5\pi}{6} = \frac{50\pi}{6} = 8\pi + \frac{2\pi}{3}.$$

Таким образом:

$$z_2^{10} = \cos \left( \frac{2\pi}{3} \right) + i \sin \left( \frac{2\pi}{3} \right).$$

Умножим $z_1^{11}$ и $z_2^{10}$:

$$z = z_1^{11} z_2^{10} = 1 \cdot 1 \left( \cos \left( -\frac{\pi}{3} + \frac{2\pi}{3} \right) + i \sin \left( -\frac{\pi}{3} + \frac{2\pi}{3} \right) \right).$$

Выполнив сложение углов:

$$-\frac{\pi}{3} + \frac{2\pi}{3} = \frac{\pi}{3}.$$

Таким образом:

$$z = \cos \frac{\pi}{3} + i \sin \frac{\pi}{3} = 1 + 0i.$$

Ответ: $\arg z = 0$.