Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 34.42 Профильный Уровень Мордкович — Подробные Ответы
а) Изобразите на комплексной плоскости множество чисел , удовлетворяющих условию . Чему равно наибольшее значение ?
б) Изобразите на комплексной плоскости множество чисел , удовлетворяющих условию . Чему равно наименьшее значение ?
а) ;
;
;
;
;
;
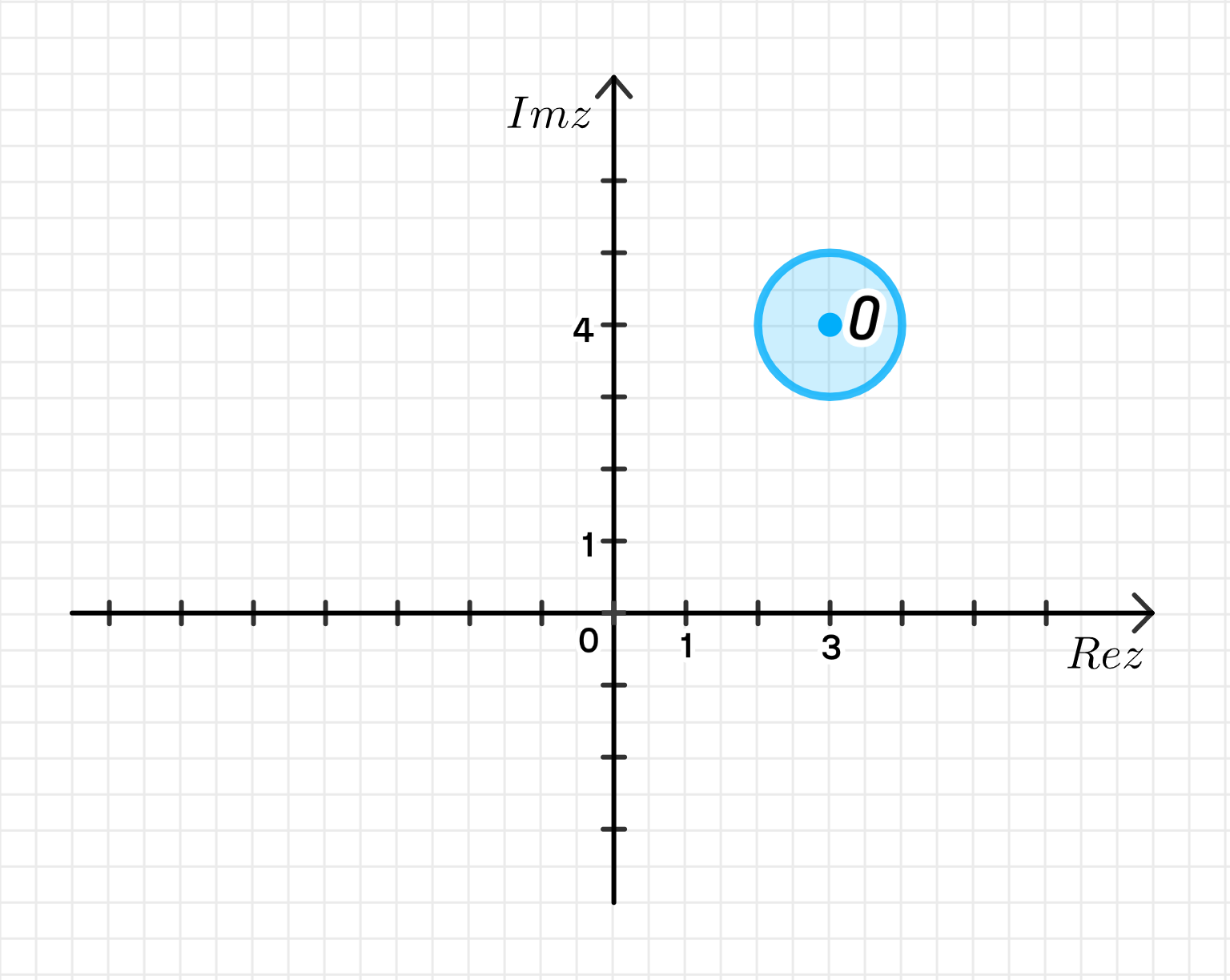
На комплексной плоскости:
Расстояние от точки до наиболее удаленной точки:
Ответ: .
б) ;
;
;
;
;
;
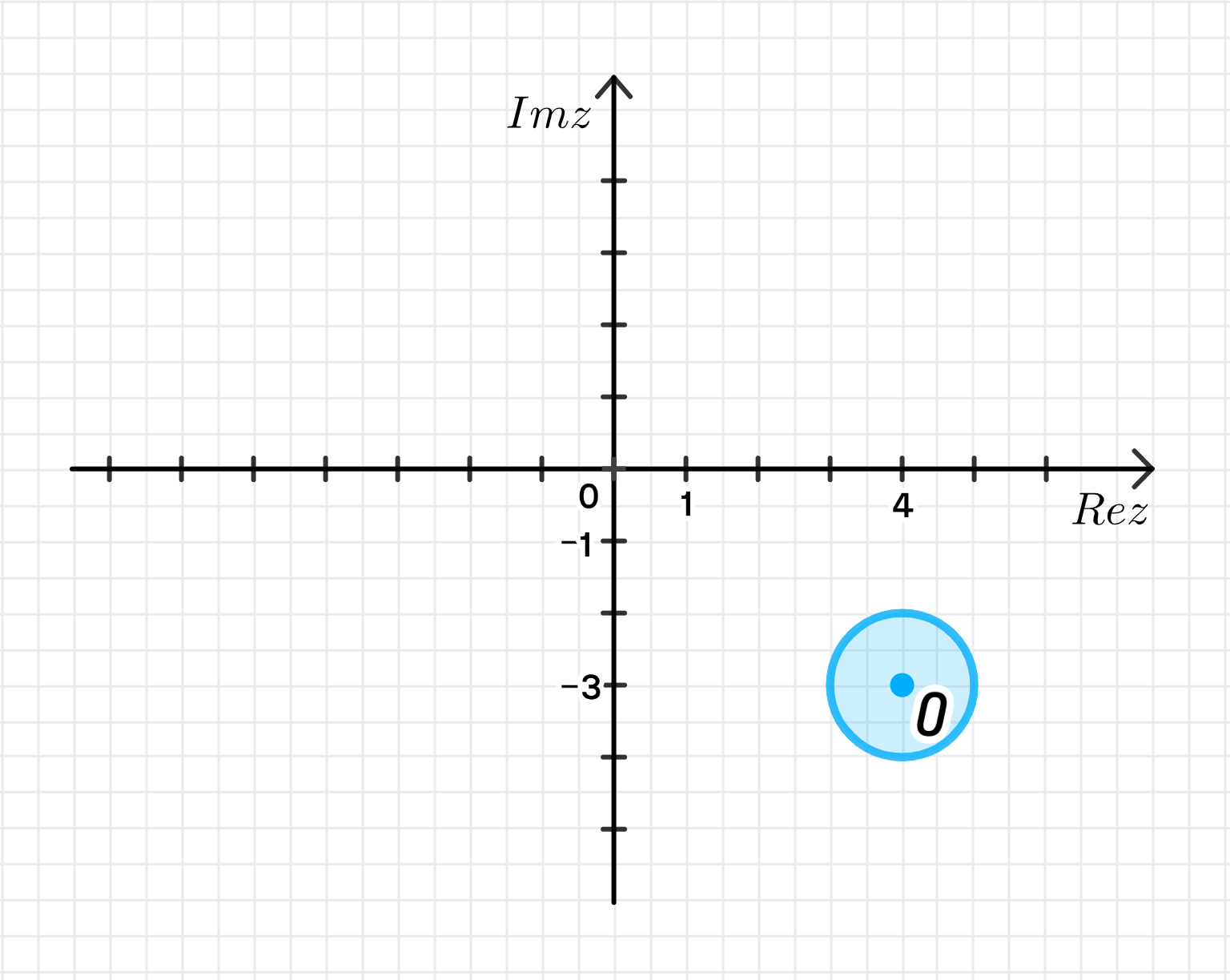
На комплексной плоскости:
Расстояние от точки до наименее удаленной точки:
Ответ: .
а) Разбор выражения:
Задание:
.
Преобразуем выражение для комплексного числа:
Пусть , где и — действительная и мнимая части комплексного числа , соответственно.
Тогда:
Теперь подставим это в неравенство:
Это можно записать как:
Мы ищем модуль этого выражения, который по определению равен:
Из условия задачи:
Это модуль комплексного числа . Вычислим его:
Это равно:
Таким образом, неравенство примет вид:
Это неравенство описывает круг на комплексной плоскости с центром в точке и радиусом 1, так как оно имеет вид:
Таким образом, множество всех таких точек на комплексной плоскости — это круг с центром в точке и радиусом 1.
1) График на комплексной плоскости:
На графике будет изображен круг с центром в точке и радиусом 1. Этот круг ограничивает область, внутри которой расположены все точки, удовлетворяющие неравенству.
2) Расстояние от точки до наиболее удаленной точки:
Пусть точка — это начало координат, то есть . Мы ищем расстояние от точки до наиболее удаленной точки на круге.
Для этого вычислим расстояние от точки до центра круга :
Теперь, так как радиус круга равен 1, наиболее удаленная точка будет находиться на расстоянии:
Ответ: .
б) Разбор выражения:
Задание:
.
Преобразуем выражение для комплексного числа:
Пусть , где и — действительная и мнимая части комплексного числа , соответственно.
Тогда:
Теперь подставим это в неравенство:
Это можно записать как:
Мы ищем модуль этого выражения, который по определению равен:
Из условия задачи:
Это модуль комплексного числа . Вычислим его:
Это равно:
Таким образом, неравенство примет вид:
Это неравенство описывает круг на комплексной плоскости с центром в точке и радиусом 1, так как оно имеет вид:
Таким образом, множество всех таких точек на комплексной плоскости — это круг с центром в точке и радиусом 1.
1) График на комплексной плоскости:
На графике будет изображен круг с центром в точке и радиусом 1. Этот круг ограничивает область, внутри которой расположены все точки, удовлетворяющие неравенству.
2) Расстояние от точки до наименее удаленной точки:
Пусть точка — это начало координат, то есть . Мы ищем расстояние от точки до наименее удаленной точки на круге.
Для этого вычислим расстояние от точки до центра круга :
Теперь, так как радиус круга равен 1, наименее удаленная точка будет находиться на расстоянии:
Ответ: .