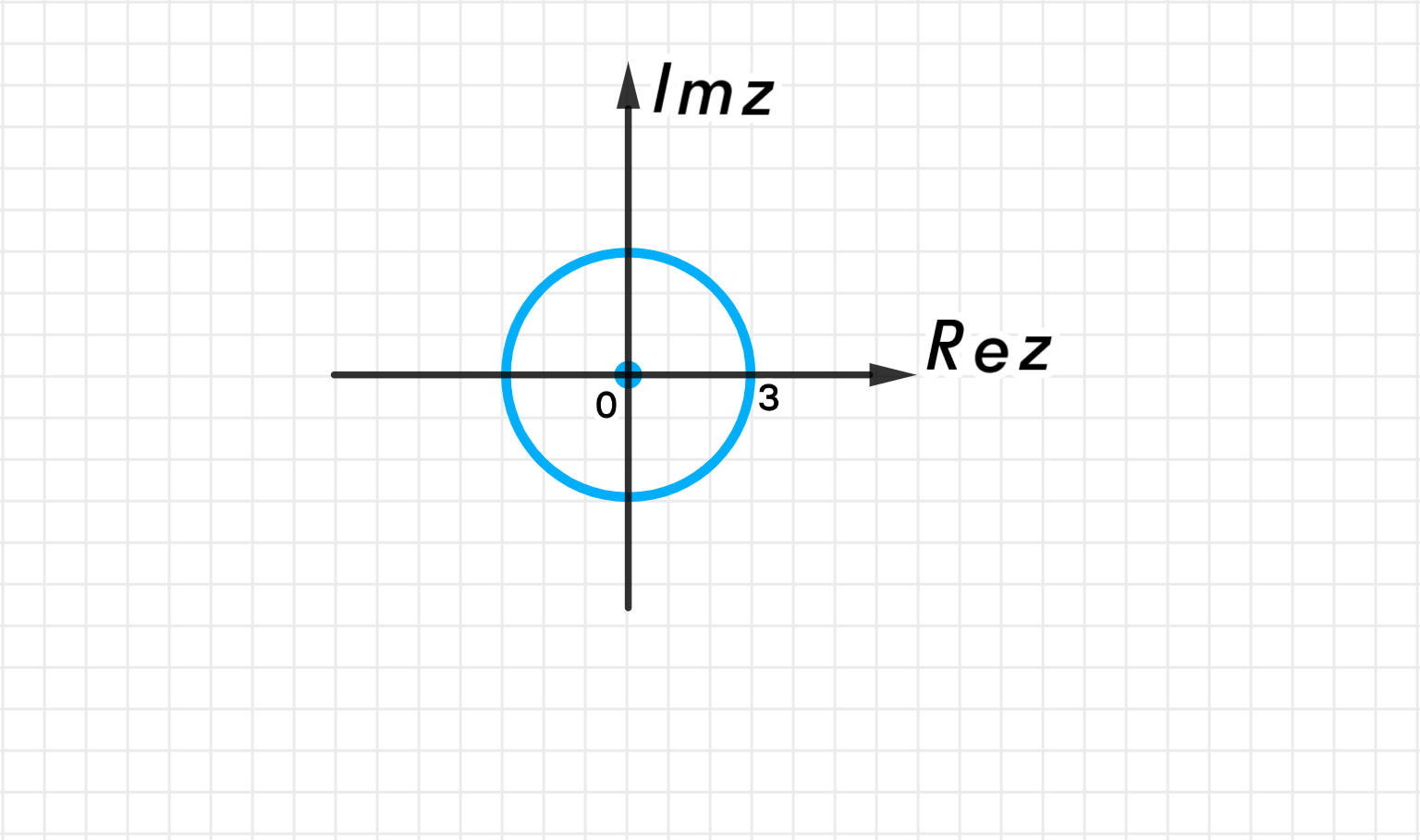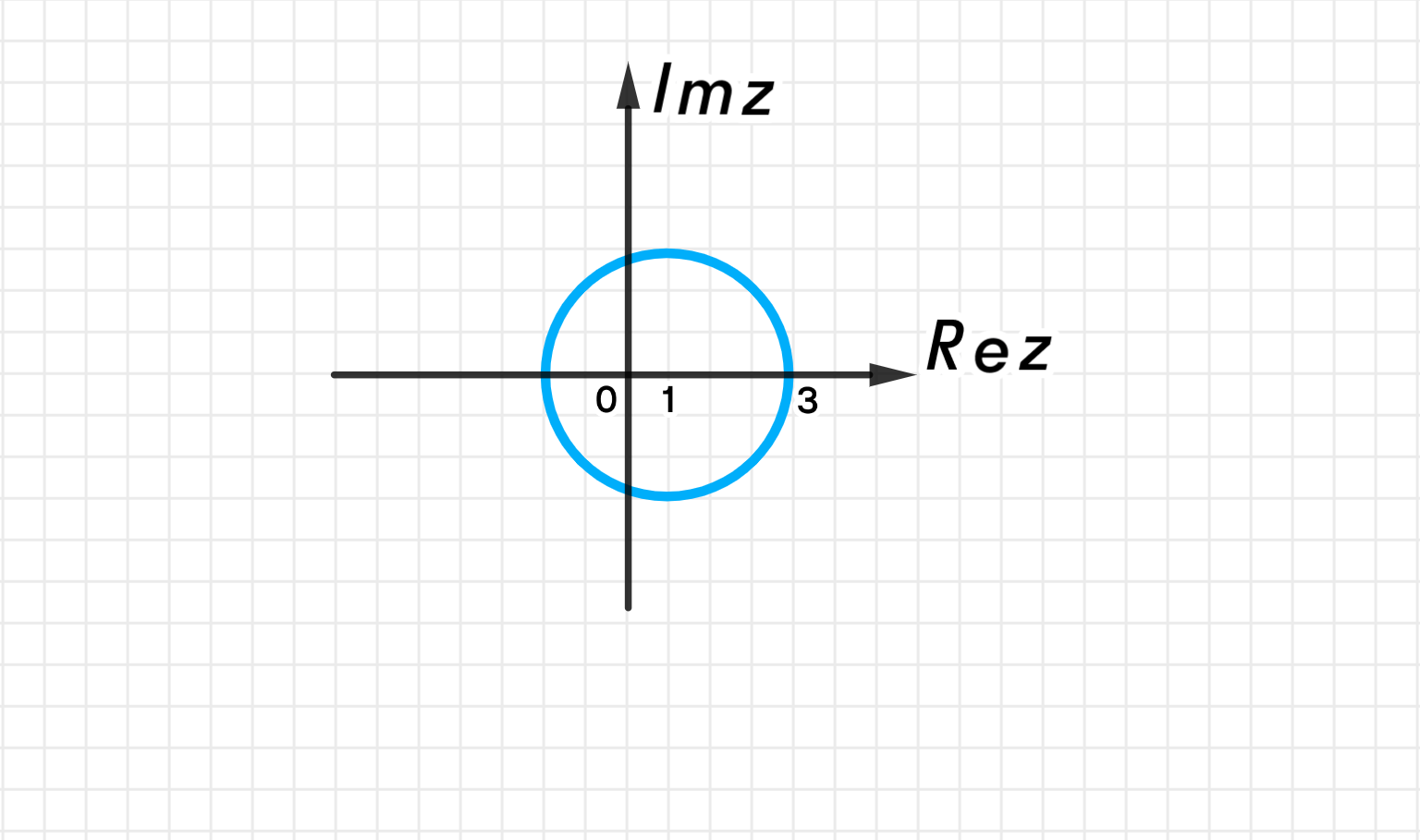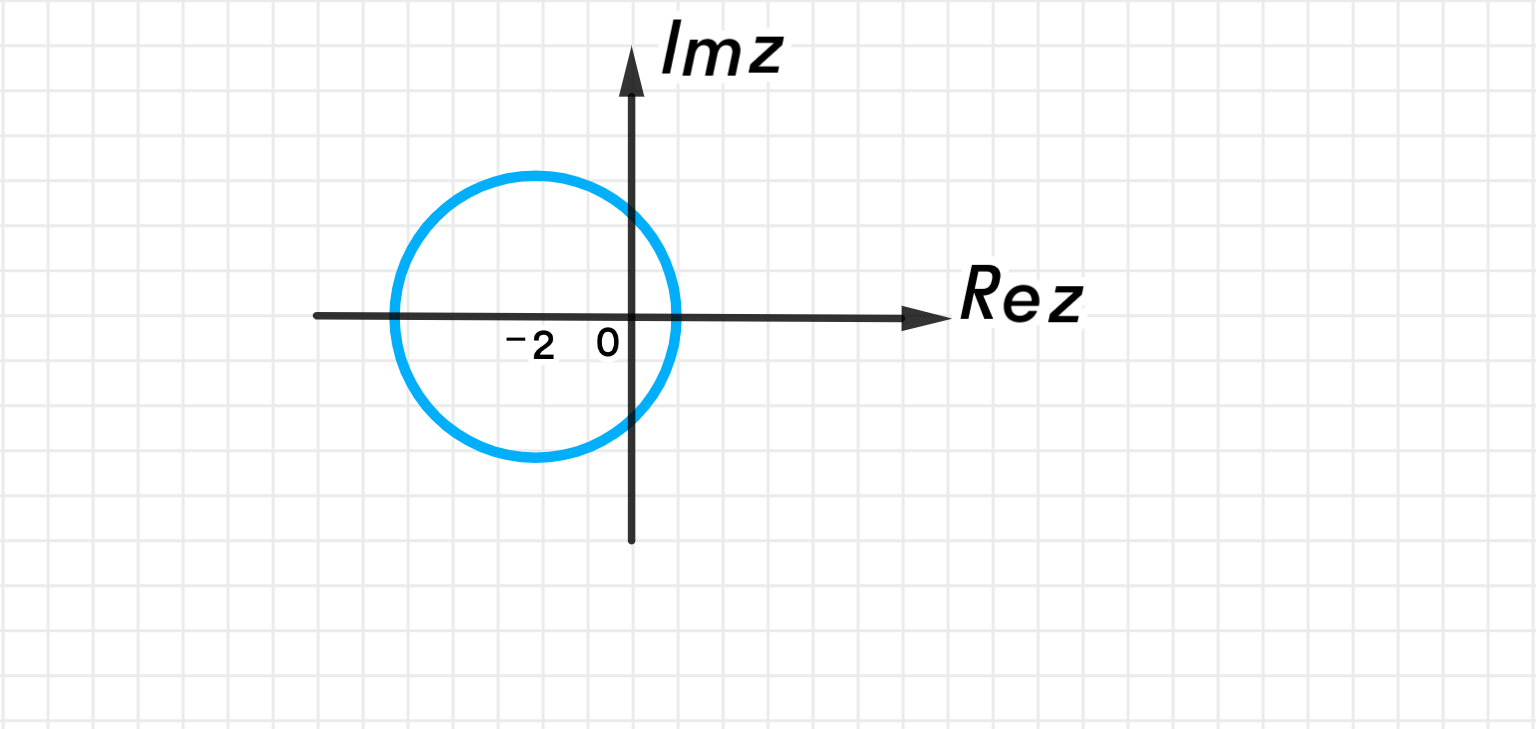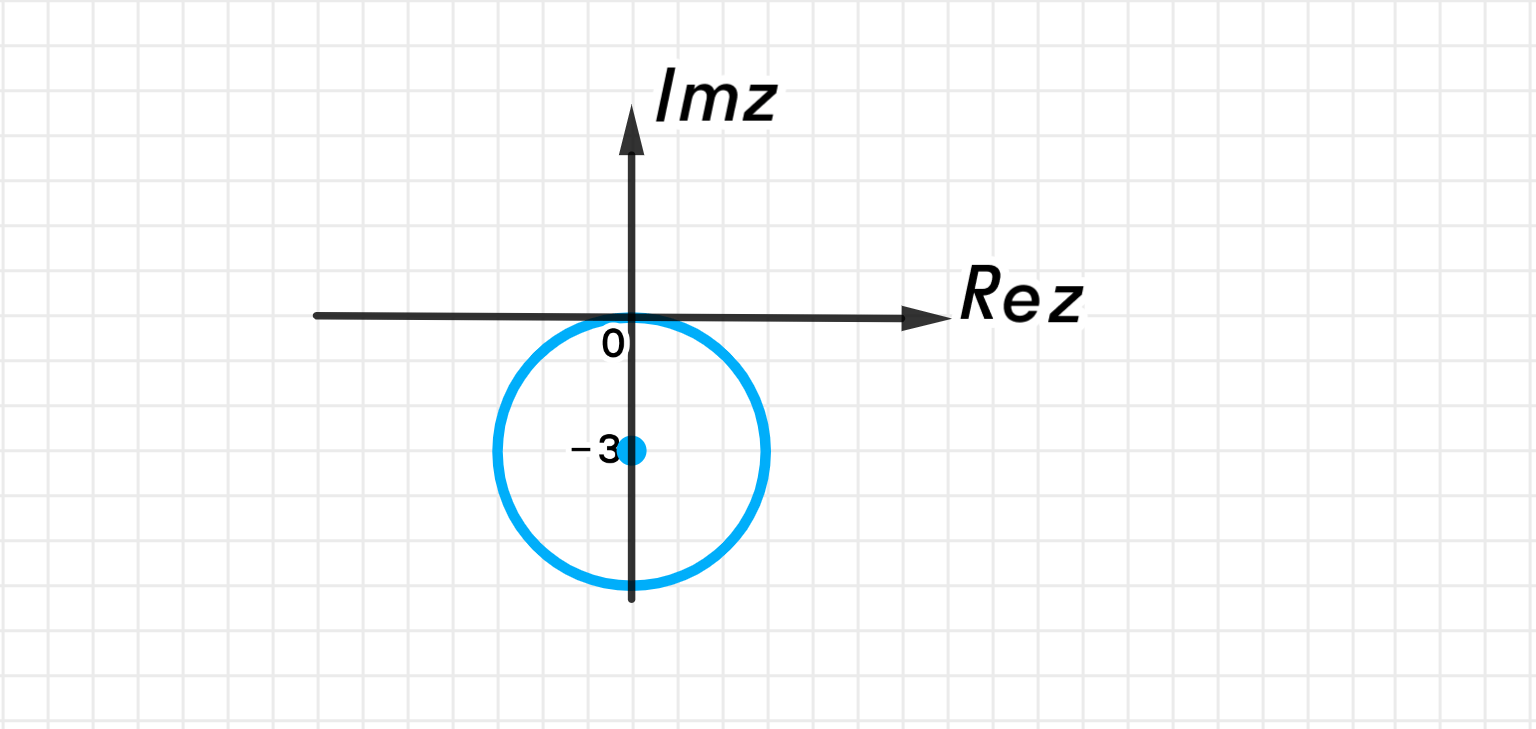ГДЗ по Алгебре 10 Класс Номер 34.6 Профильный Уровень Мордкович — Подробные Ответы

Изобразите на комплексной плоскости множество всех чисел z, удовлетворяющих заданному условию:

a) |z| = 3;

б) |z — 1| = 3;

в) |z + 2| = 3;

г) |z + 3i| = 3.

Изобразить на комплексной плоскости множество всех чисел $z$, удовлетворяющих заданному условию:

а) $|z| = 3$;
$|x + yi| = 3$;
$\sqrt{x^2 + y^2} = 3$;
$x^2 + y^2 = 3^2$;

б) $|z — 1| = 3$;
$|x + yi — 1| = 3$;
$\sqrt{(x — 1)^2 + y^2} = 3$;
$(x — 1)^2 + y^2 = 3^2$;

в) $|z + 2| = 3$;
$|x + yi + 2| = 3$;
$\sqrt{(x + 2)^2 + y^2} = 3$;
$(x + 2)^2 + y^2 = 3^2$;

г) $|z + 3i| = 3$;
$|x + yi + 3i| = 3$;
$\sqrt{x^2 + (y + 3)^2} = 3$;
$x^2 + (y + 3)^2 = 3^2$;

а) $|z| = 3$

1. Начнем с определения модуля комплексного числа:

$z = x + yi \Rightarrow |z| = \sqrt{x^2 + y^2}$

2. Подставим в условие:

$|z| = 3 \Rightarrow \sqrt{x^2 + y^2} = 3$

3. Возведем обе части в квадрат:

$x^2 + y^2 = 9$

Геометрический смысл:

Это окружность радиуса 3 с центром в начале координат (0, 0).

б) $|z — 1| = 3$

1. Запишем $z$ как $x + yi$, тогда:

$$|z — 1| = |x + yi — 1| = |(x — 1) + yi| = \sqrt{(x — 1)^2 + y^2}$$

2. По условию:

$$\sqrt{(x — 1)^2 + y^2} = 3$$

3. Возведем в квадрат:

$$(x — 1)^2 + y^2 = 9$$

Геометрический смысл:

Это окружность радиуса 3 с центром в точке $(1, 0)$.

в) $|z + 2| = 3$

1. Запишем $z = x + yi$, тогда:

$$|z + 2| = |x + yi + 2| = |(x + 2) + yi| = \sqrt{(x + 2)^2 + y^2}$$

2. По условию:

$$\sqrt{(x + 2)^2 + y^2} = 3$$

3. Возводим в квадрат:

$$(x + 2)^2 + y^2 = 9$$

Геометрический смысл:

Это окружность радиуса 3 с центром в точке $(-2, 0)$.

г) $|z + 3i| = 3$

1. Представим $z = x + yi$, тогда:

$$|z + 3i| = |x + yi + 3i| = |x + (y + 3)i| = \sqrt{x^2 + (y + 3)^2}$$

2. По условию:

$$\sqrt{x^2 + (y + 3)^2} = 3$$

3. Возведем обе части в квадрат:

$$x^2 + (y + 3)^2 = 9$$

Геометрический смысл:

Это окружность радиуса 3 с центром в точке $(0, -3)$.