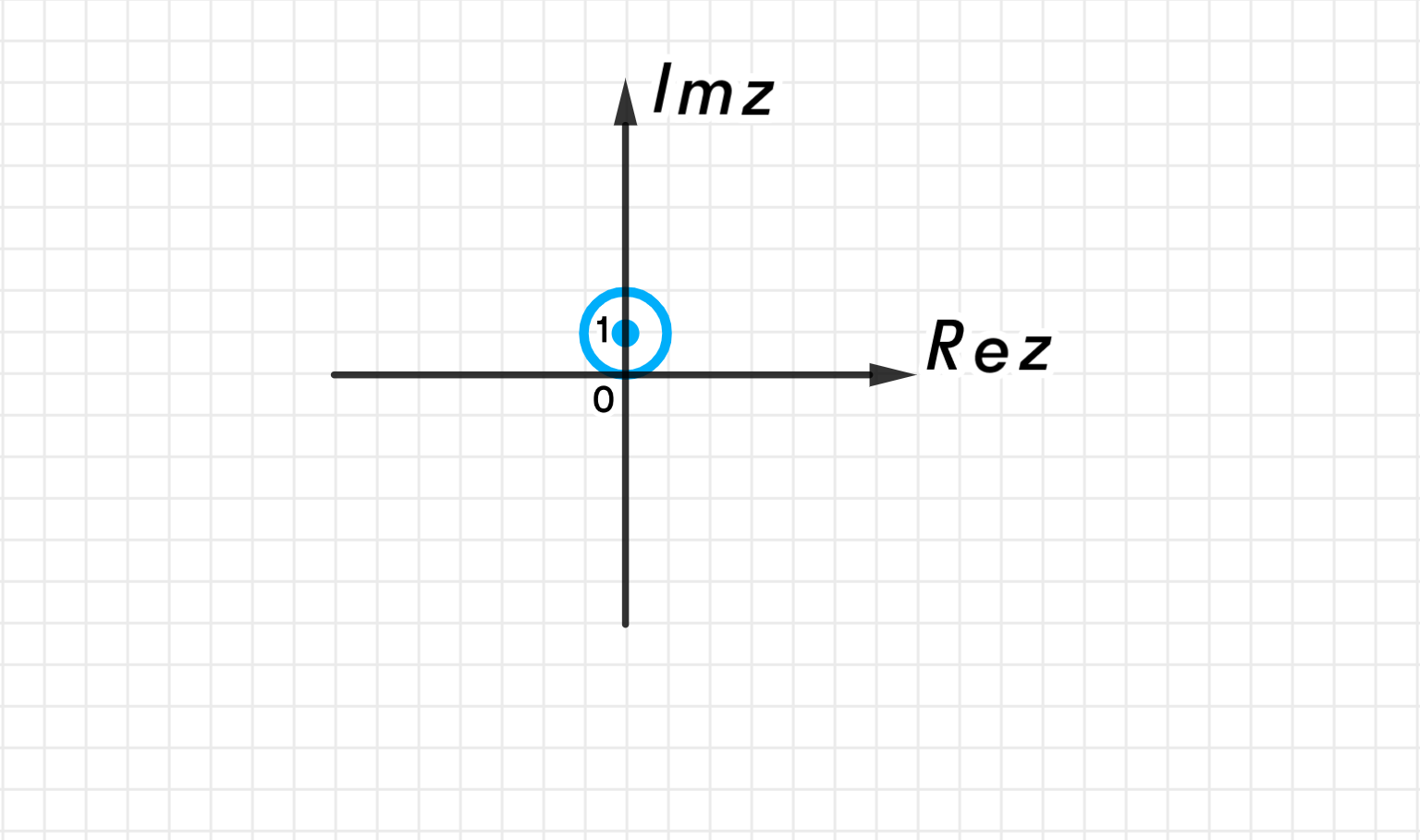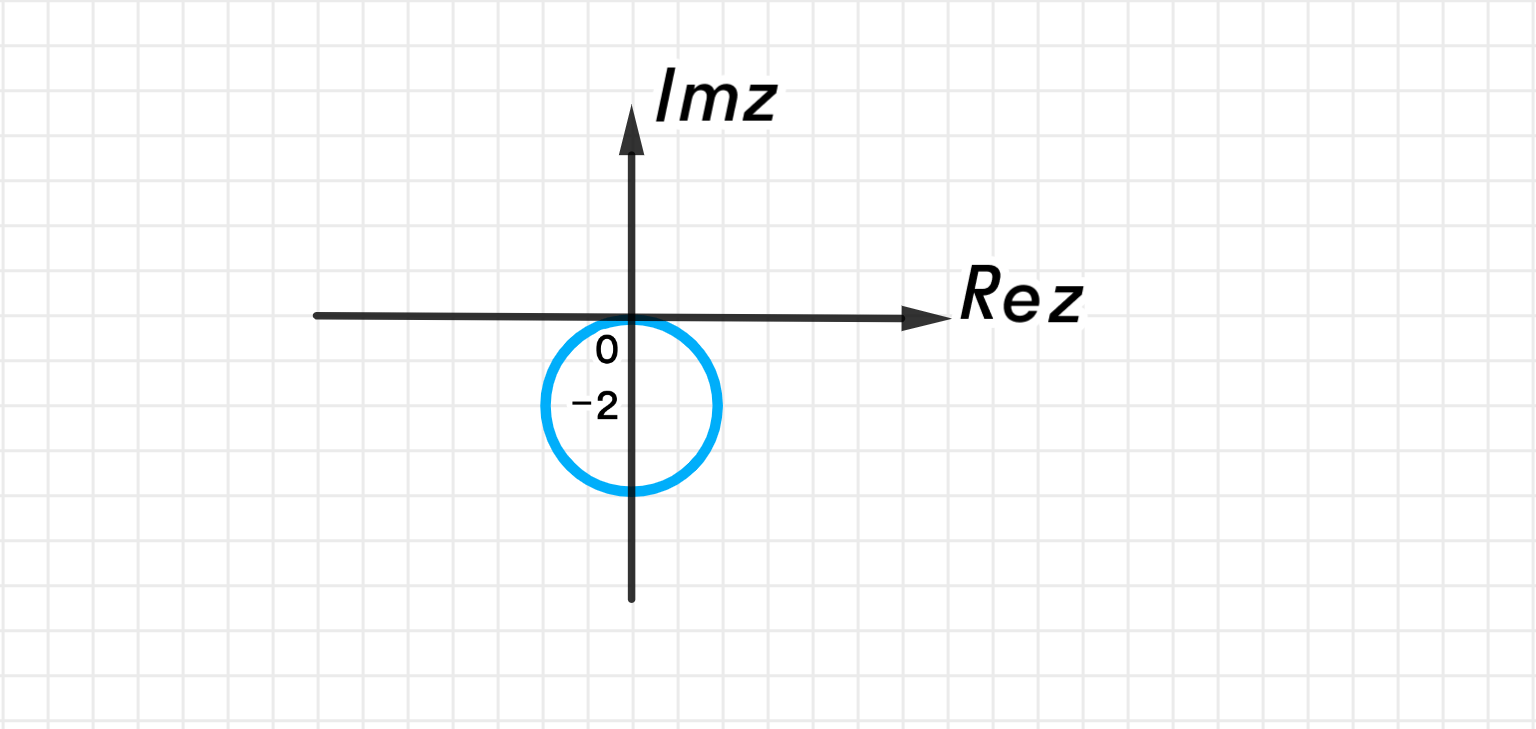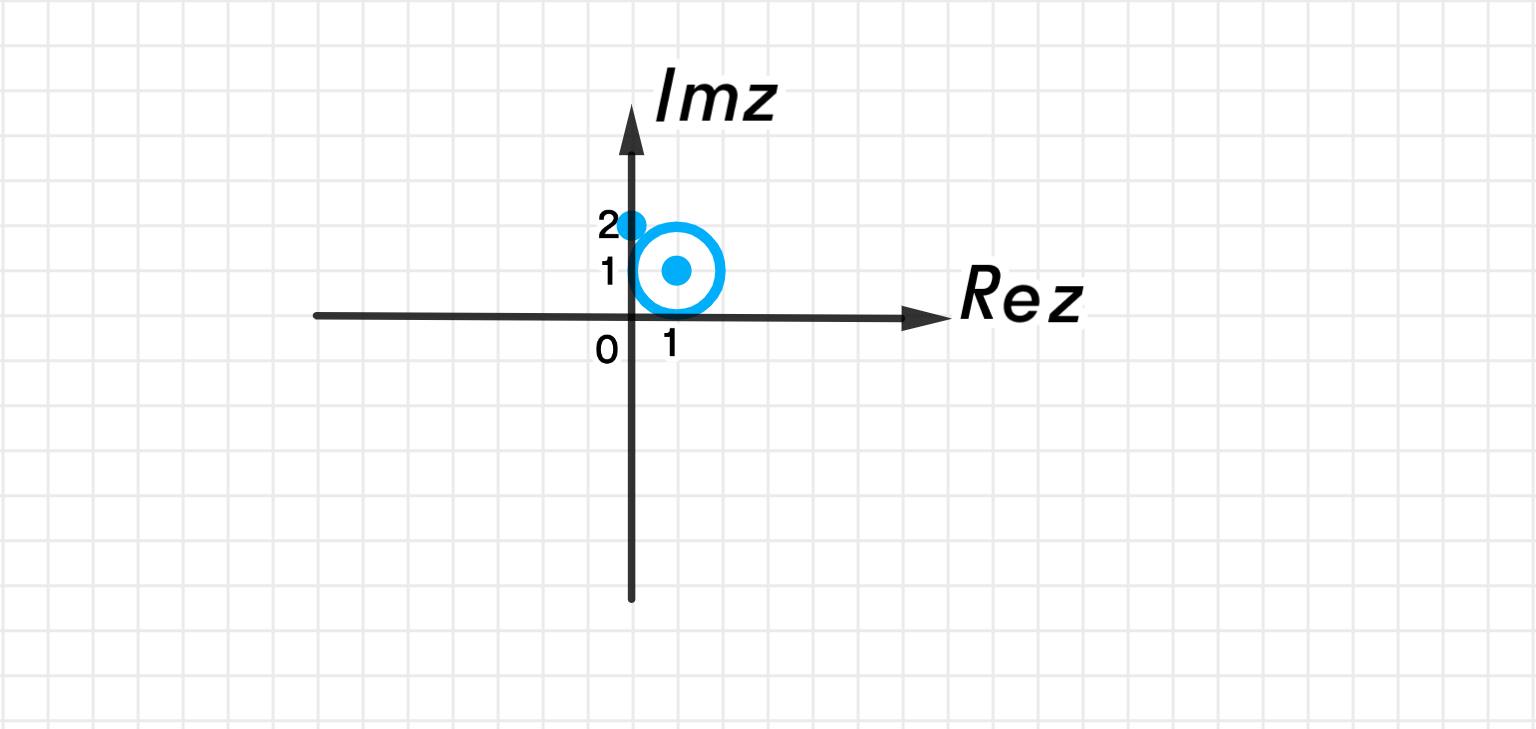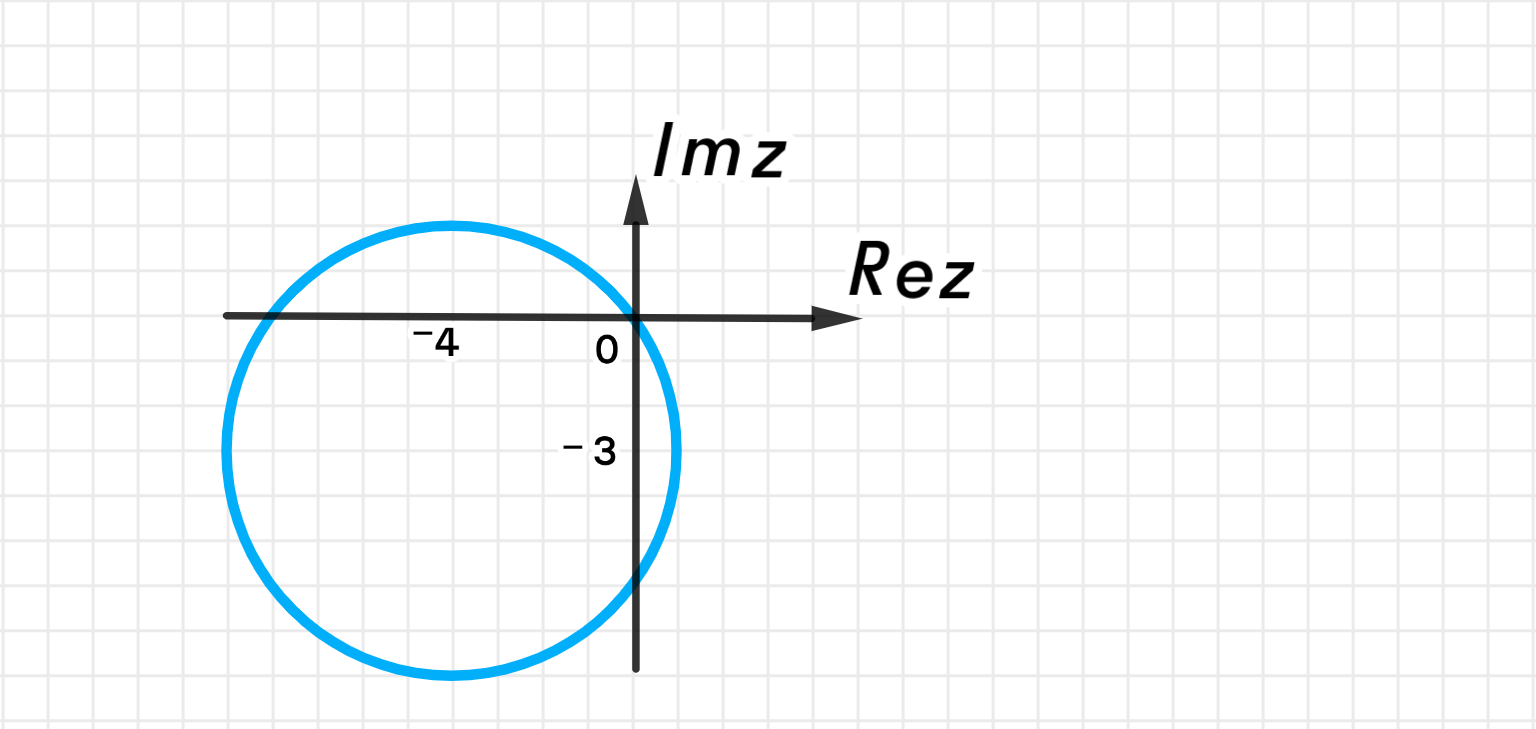ГДЗ по Алгебре 10 Класс Номер 34.7 Профильный Уровень Мордкович — Подробные Ответы

Изобразить на комплексной плоскости множество всех чисел $z$, удовлетворяющих заданному условию:

а) $|z — i| = 1$;
$\mathrm{}$$|x + yi — i| = 1$;
$\sqrt{x^2 + (y — 1)^2} = 1$;
$x^2 + (y — 1)^2 = 1^2$;

б) $|z + 2i| = 2$;
$\mathrm{}$$|x + yi + 2i| = 2$;
$\sqrt{x^2 + (y + 2)^2} = 2$;
$x^2 + (y + 2)^2 = 2^2$;

в) $|z — 1 — i| = \sqrt{2}$;
$\mathrm{}$$|x + yi — 1 — i| = \sqrt{2}$;
$\sqrt{(x — 1)^2 + (y — 1)^2} = \sqrt{2}$;
$(x — 1)^2 + (y — 1)^2 = (\sqrt{2})^2$;

г) $|z + 4 + 3i| = 5$;
$\mathrm{}$$|x + yi + 4 + 3i| = 5$;
$\sqrt{(x + 4)^2 + (y + 3)^2} = 5$;
$(x + 4)^2 + (y + 3)^2 = 5^2$;

Задано множество комплексных чисел $z$, которые удовлетворяют условиям вида:

$$|z — a| = r$$

Это означает, что геометрически $z$ находится на окружности радиуса $r$ с центром в точке $a$ на комплексной плоскости. Запишем $z = x + yi$, где $x, y \in \mathbb{R}$, тогда:

$$|z — a| = \sqrt{(x — \text{Re}(a))^2 + (y — \text{Im}(a))^2} = r$$

Поднимем это в квадрат, чтобы получить уравнение окружности в алгебраическом виде.

а) $|z — i| = 1$

Шаг 1. Запишем $z = x + yi$.
$i = 0 + 1i \Rightarrow \text{Re}(i) = 0, \text{Im}(i) = 1$

Шаг 2. Вычислим модуль:

$$|z — i| = |x + yi — i| = |x + (y — 1)i| = \sqrt{x^2 + (y — 1)^2}$$

Шаг 3. Приравниваем модуль к 1:

$$\sqrt{x^2 + (y — 1)^2} = 1$$

Шаг 4. Возводим в квадрат обе части:

$$x^2 + (y — 1)^2 = 1^2 = 1$$

Вывод: Это уравнение окружности с центром в точке $(0, 1)$, радиус $R = 1$.

б) $|z + 2i| = 2$

Шаг 1. $z = x + yi$, $+2i = 0 + 2i \Rightarrow \text{Re} = 0, \text{Im} = 2$

Шаг 2. Модуль:

$$|z + 2i| = |x + yi + 2i| = |x + (y + 2)i| = \sqrt{x^2 + (y + 2)^2}$$

Шаг 3. Приравниваем:

$$\sqrt{x^2 + (y + 2)^2} = 2$$

Шаг 4. Квадрат:

$$x^2 + (y + 2)^2 = 2^2 = 4$$

Вывод: Центр окружности в точке $(0, -2)$, радиус $R = 2$

в) $|z — 1 — i| = \sqrt{2}$

Шаг 1. $z = x + yi$, $1 + i = 1 + 1i \Rightarrow \text{Re} = 1, \text{Im} = 1$

Шаг 2. Модуль:

$$|z — (1 + i)| = |x + yi — 1 — i| = |(x — 1) + (y — 1)i| = \sqrt{(x — 1)^2 + (y — 1)^2}$$

Шаг 3. Приравниваем:

$$\sqrt{(x — 1)^2 + (y — 1)^2} = \sqrt{2}$$

Шаг 4. Квадрат:

$$(x — 1)^2 + (y — 1)^2 = 2$$

Вывод: Центр окружности $(1, 1)$, радиус $R = \sqrt{2}$

г) $|z + 4 + 3i| = 5$

Шаг 1. $z = x + yi$, $+4 + 3i = -4 — 3i \Rightarrow \text{Re} = -4, \text{Im} = -3$

Шаг 2. Модуль:

$$|z + 4 + 3i| = |x + yi + 4 + 3i| = |(x + 4) + (y + 3)i| = \sqrt{(x + 4)^2 + (y + 3)^2}$$

Шаг 3. Приравниваем:

$$\sqrt{(x + 4)^2 + (y + 3)^2} = 5$$

Шаг 4. Квадрат:

$$(x + 4)^2 + (y + 3)^2 = 25$$

Вывод: Центр окружности $(-4, -3)$, радиус $R = 5$