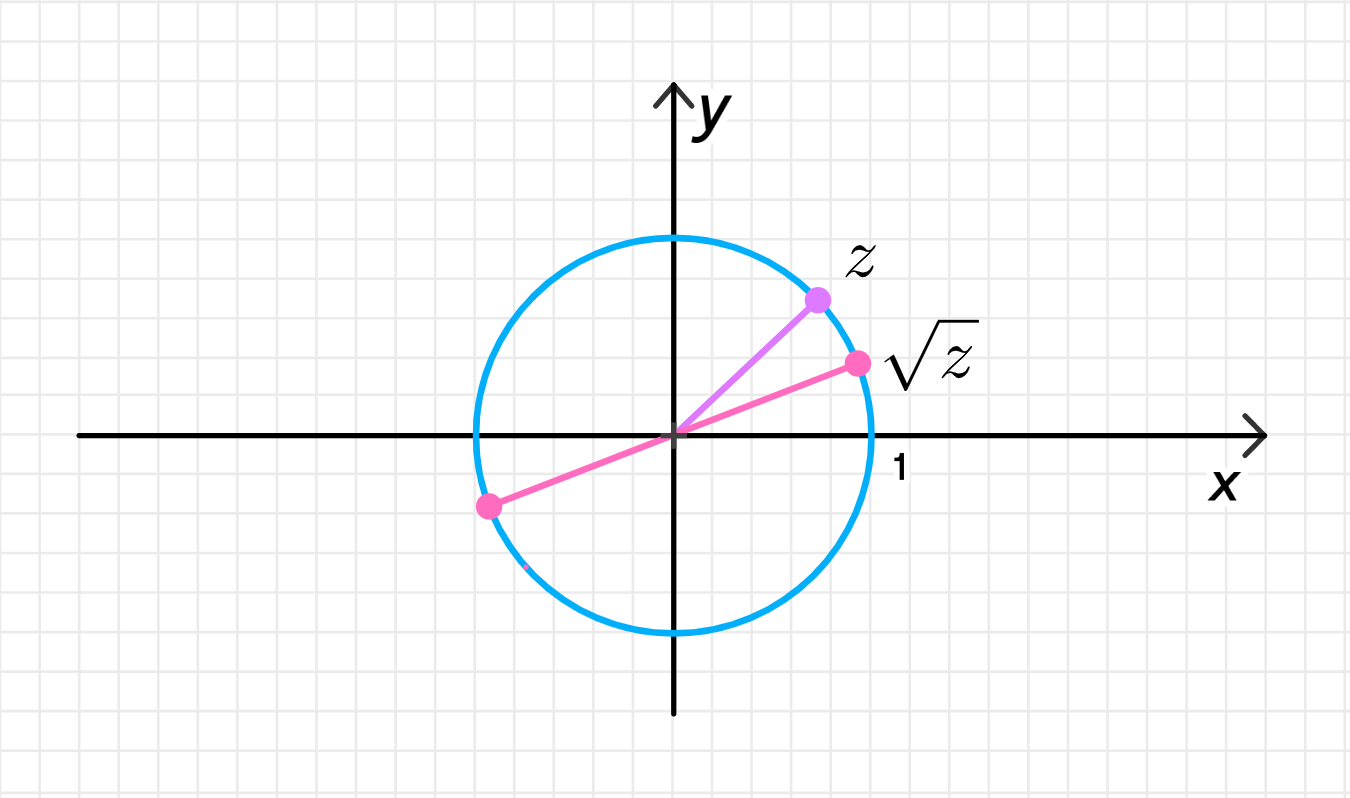ГДЗ по Алгебре 10 Класс Номер 35.15 Профильный Уровень Мордкович — Подробные Ответы

Изобразить на комплексной плоскости число $z$ и множество $\sqrt{z}$, если:

а) $|z| = 1$, $\arg(z) = \frac{\pi}{4}$;

$$z = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} = \cos 45^\circ + i \sin 45^\circ;$$ $$\sqrt{z} = \pm \sqrt{1} \left( \cos \frac{\pi}{8} + i \sin \frac{\pi}{8} \right) = \pm (\cos 22.5^\circ + i \sin 22.5^\circ);$$

Данные числа на комплексной плоскости:

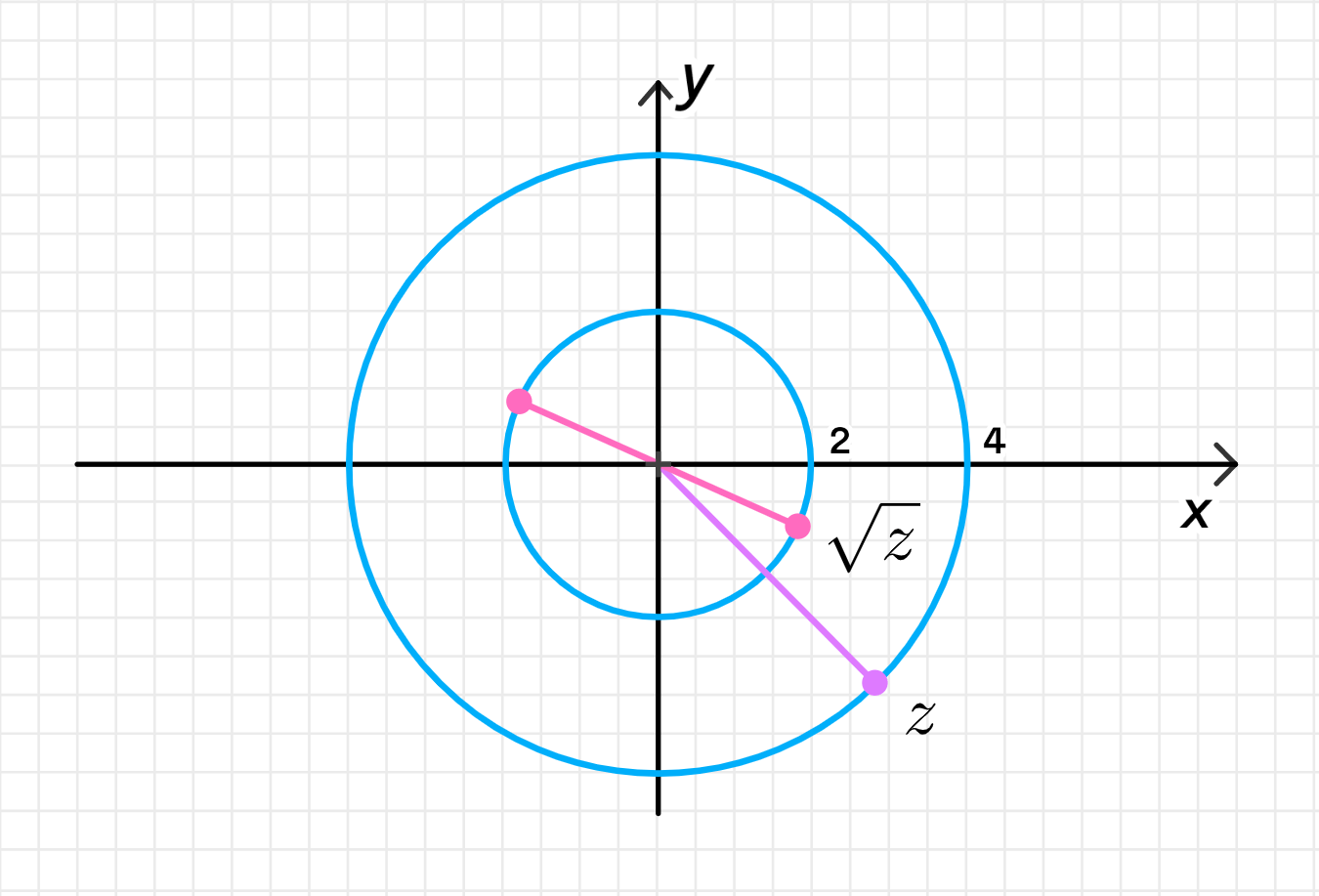
б) $|z| = 4$, $\arg(z) = -\frac{\pi}{4}$;

$$z = 4 \left( \cos \left( -\frac{\pi}{4} \right) + i \sin \left( -\frac{\pi}{4} \right) \right) = 4 (\cos(-45^\circ) + i \sin(-45^\circ));$$ $$\sqrt{z} = \pm \sqrt{4} \left( \cos \left( -\frac{\pi}{8} \right) + i \sin \left( -\frac{\pi}{8} \right) \right) = \pm 2 (\cos(-22.5^\circ) + i \sin(-22.5^\circ));$$

Данные числа на комплексной плоскости:

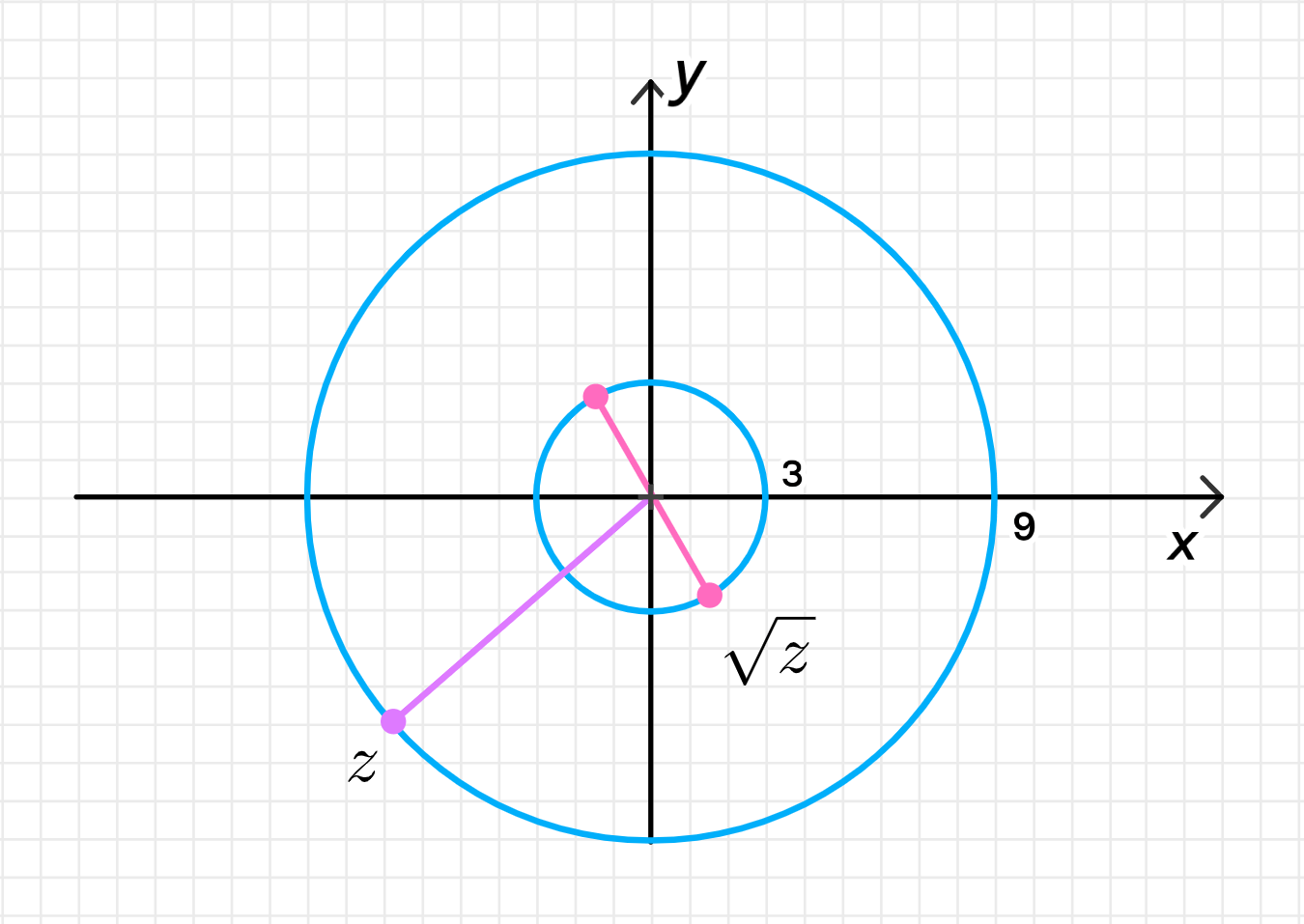
в) $|z| = 9$, $\arg(z) = -\frac{3\pi}{4}$;

$$z = 9 \left( \cos \left( -\frac{3\pi}{4} \right) + i \sin \left( -\frac{3\pi}{4} \right) \right) = 9 (\cos(-135^\circ) + i \sin(-135^\circ));$$ $$\sqrt{z} = \pm \sqrt{9} \left( \cos \left( -\frac{3\pi}{8} \right) + i \sin \left( -\frac{3\pi}{8} \right) \right) = \pm 3 (\cos(-67.5^\circ) + i \sin(-67.5^\circ));$$

Данные числа на комплексной плоскости:

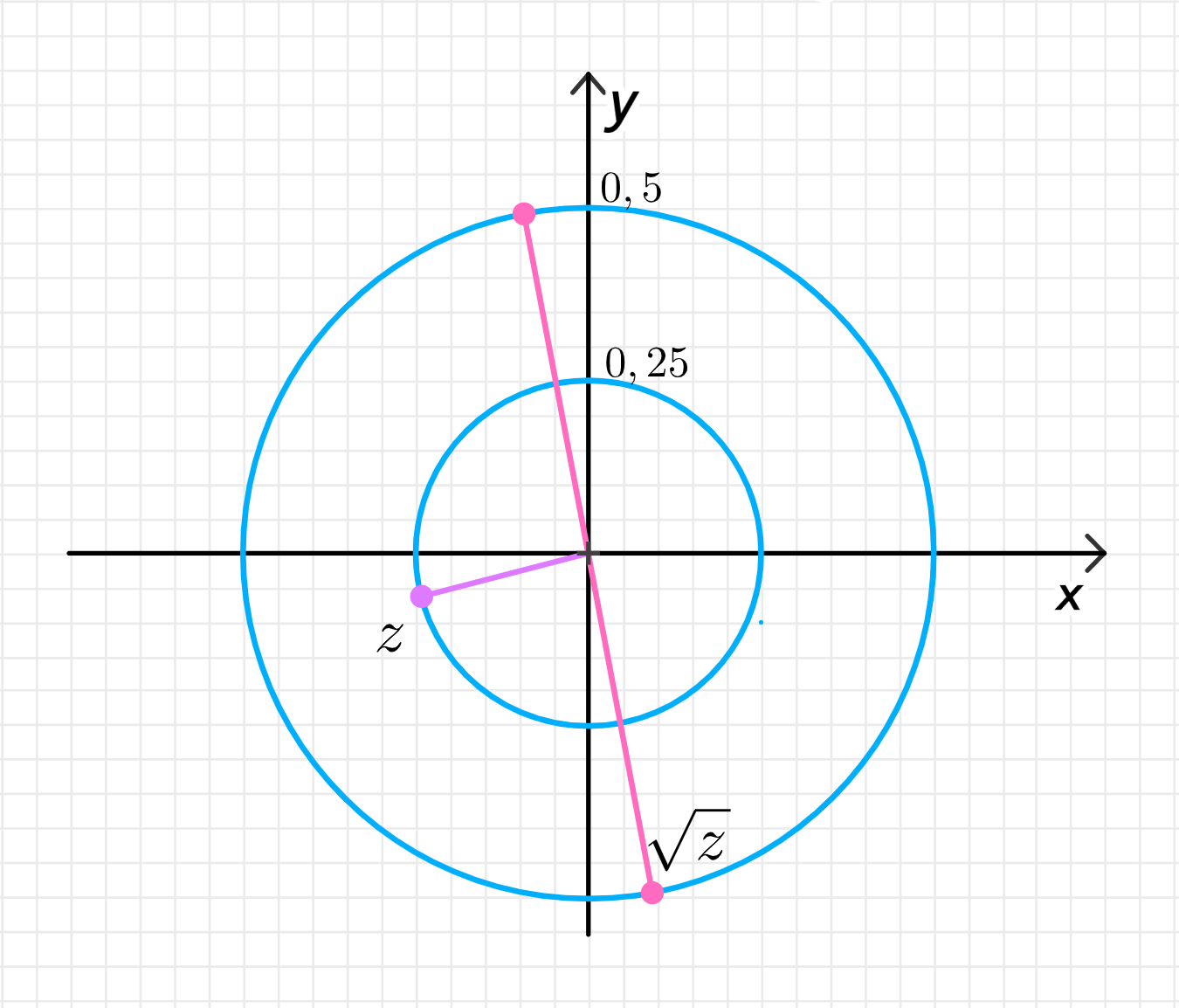
г) $|z| = 0.25$, $\arg(z) = -\frac{9\pi}{10}$;

$$z = \frac{1}{4} \left( \cos \left( -\frac{9\pi}{10} \right) + i \sin \left( -\frac{9\pi}{10} \right) \right) = \frac{1}{4} (\cos(-162^\circ) + i \sin(-162^\circ));$$ $$\sqrt{z} = \pm \sqrt{\frac{1}{4}} \left( \cos \left( -\frac{9\pi}{20} \right) + i \sin \left( -\frac{9\pi}{20} \right) \right) = \pm \frac{1}{2} (\cos(-81^\circ) + i \sin(-81^\circ));$$

Данные числа на комплексной плоскости:

Каждое комплексное число можно представить в виде:

$$z = r \left( \cos \varphi + i \sin \varphi \right),$$

где:

$r$ — модуль числа, $r = |z|$,

$\varphi$ — аргумент числа, $\arg(z)$,

$i$ — мнимая единица.

Корень из комплексного числа $z$ извлекается по аналогичной формуле:

$$\sqrt{z} = \pm \sqrt{r} \left( \cos \frac{\varphi}{2} + i \sin \frac{\varphi}{2} \right).$$

Мы будем использовать это представление для каждого случая задачи.

а) $|z| = 1$, $\arg(z) = \frac{\pi}{4}$

Запишем число $z$:

$$z = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4}.$$

Известно, что $\cos \frac{\pi}{4} = \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2}$, поэтому:

$$z = \frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2}.$$

Найдем корни числа $z$:
Модуль числа $z$ равен $1$, поэтому $\sqrt{z}$ будет:

$$\sqrt{z} = \pm \sqrt{1} \left( \cos \frac{\pi}{8} + i \sin \frac{\pi}{8} \right) = \pm \left( \cos 22.5^\circ + i \sin 22.5^\circ \right).$$

Таким образом, два корня:

$$\sqrt{z} = \pm \left( \cos 22.5^\circ + i \sin 22.5^\circ \right).$$

Изображение на комплексной плоскости:

• Точка $z$ будет находиться на окружности радиусом 1 и углом $\frac{\pi}{4}$ от положительного направления оси $x$.
• Множество $\sqrt{z}$ будет содержать два числа, одно с углом $22.5^\circ$, а другое с углом $22.5^\circ + 180^\circ = 202.5^\circ$.

б) $|z| = 4$, $\arg(z) = -\frac{\pi}{4}$

Запишем число $z$:

$$z = 4 \left( \cos \left( -\frac{\pi}{4} \right) + i \sin \left( -\frac{\pi}{4} \right) \right).$$

Так как $\cos \left( -\frac{\pi}{4} \right) = \sin \left( -\frac{\pi}{4} \right) = -\frac{\sqrt{2}}{2}$, получаем:

$$z = 4 \left( -\frac{\sqrt{2}}{2} + i \left( -\frac{\sqrt{2}}{2} \right) \right) = -2\sqrt{2} — 2\sqrt{2} i.$$

Найдем корни числа $z$:
Модуль числа $z$ равен $4$, а аргумент $z$ равен $-\frac{\pi}{4}$. Следовательно, корни будут:

$$\sqrt{z} = \pm \sqrt{4} \left( \cos \left( -\frac{\pi}{8} \right) + i \sin \left( -\frac{\pi}{8} \right) \right).$$

Модуль $\sqrt{z}$ равен $2$, а углы:

$$\sqrt{z} = \pm 2 \left( \cos \left( -22.5^\circ \right) + i \sin \left( -22.5^\circ \right) \right).$$

Это означает два корня на окружности радиусом 2, с углами $-22.5^\circ$ и $157.5^\circ$.

Изображение на комплексной плоскости:

• Точка $z$ будет находиться на окружности радиусом 4 и углом $-45^\circ$.
• Множество $\sqrt{z}$ будет содержать два числа на окружности радиусом 2, с углами $-22.5^\circ$ и $157.5^\circ$.

в) $|z| = 9$, $\arg(z) = -\frac{3\pi}{4}$

Запишем число $z$:

$$z = 9 \left( \cos \left( -\frac{3\pi}{4} \right) + i \sin \left( -\frac{3\pi}{4} \right) \right).$$

Так как $\cos \left( -\frac{3\pi}{4} \right) = -\frac{\sqrt{2}}{2}$ и $\sin \left( -\frac{3\pi}{4} \right) = -\frac{\sqrt{2}}{2}$, получаем:

$$z = 9 \left( -\frac{\sqrt{2}}{2} + i \left( -\frac{\sqrt{2}}{2} \right) \right) = -\frac{9\sqrt{2}}{2} — \frac{9\sqrt{2}}{2} i.$$

Найдем корни числа $z$:
Модуль числа $z$ равен $9$, а аргумент $z$ равен $-\frac{3\pi}{4}$. Следовательно, корни будут:

$$\sqrt{z} = \pm \sqrt{9} \left( \cos \left( -\frac{3\pi}{8} \right) + i \sin \left( -\frac{3\pi}{8} \right) \right).$$

Модуль $\sqrt{z}$ равен $3$, а углы:

$$\sqrt{z} = \pm 3 \left( \cos \left( -67.5^\circ \right) + i \sin \left( -67.5^\circ \right) \right).$$

Это означает два корня на окружности радиусом 3, с углами $-67.5^\circ$ и $112.5^\circ$.

Изображение на комплексной плоскости:

• Точка $z$ будет находиться на окружности радиусом 9 и углом $-135^\circ$.
• Множество $\sqrt{z}$ будет содержать два числа на окружности радиусом 3, с углами $-67.5^\circ$ и $112.5^\circ$.

г) $|z| = 0.25$, $\arg(z) = -\frac{9\pi}{10}$

Запишем число $z$:

$$z = \frac{1}{4} \left( \cos \left( -\frac{9\pi}{10} \right) + i \sin \left( -\frac{9\pi}{10} \right) \right).$$

Так как $\cos \left( -\frac{9\pi}{10} \right) = -0.809$ и $\sin \left( -\frac{9\pi}{10} \right) = -0.588$, получаем:

$$z = \frac{1}{4} \left( -0.809 + i(-0.588) \right) = -0.202 + i(-0.147).$$

Найдем корни числа $z$:
Модуль числа $z$ равен $0.25$, а аргумент $z$ равен $-\frac{9\pi}{10}$. Следовательно, корни будут:

$$\sqrt{z} = \pm \sqrt{0.25} \left( \cos \left( -\frac{9\pi}{20} \right) + i \sin \left( -\frac{9\pi}{20} \right) \right).$$

Модуль $\sqrt{z}$ равен $0.5$, а углы:

$$\sqrt{z} = \pm 0.5 \left( \cos \left( -81^\circ \right) + i \sin \left( -81^\circ \right) \right).$$

Это означает два корня на окружности радиусом 0.5, с углами $-81^\circ$ и $99^\circ$.

Изображение на комплексной плоскости:

• Точка $z$ будет находиться на окружности радиусом 0.25 и углом $-162^\circ$.
• Множество $\sqrt{z}$ будет содержать два числа на окружности радиусом 0.5, с углами $-81^\circ$ и $99^\circ$.