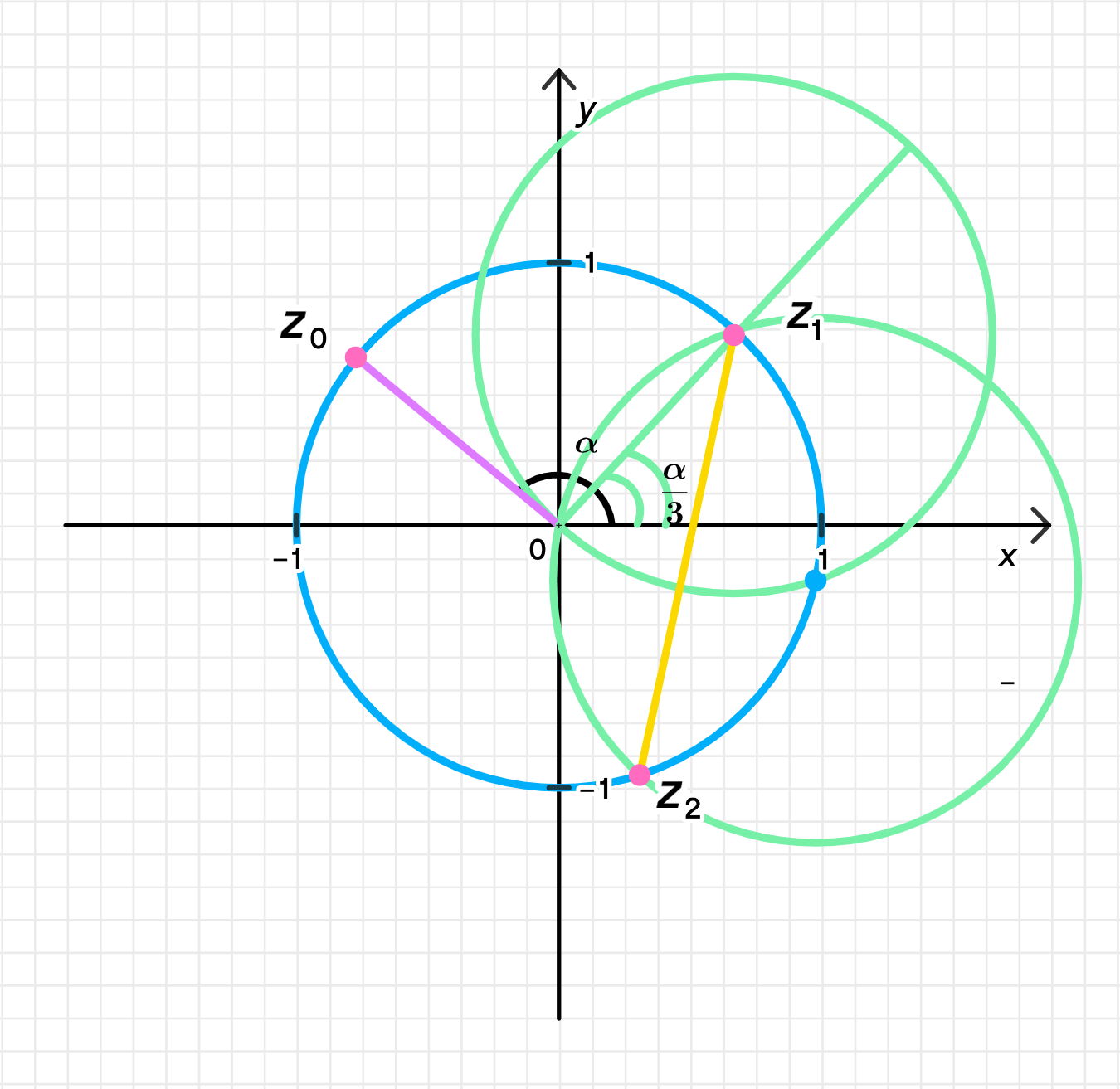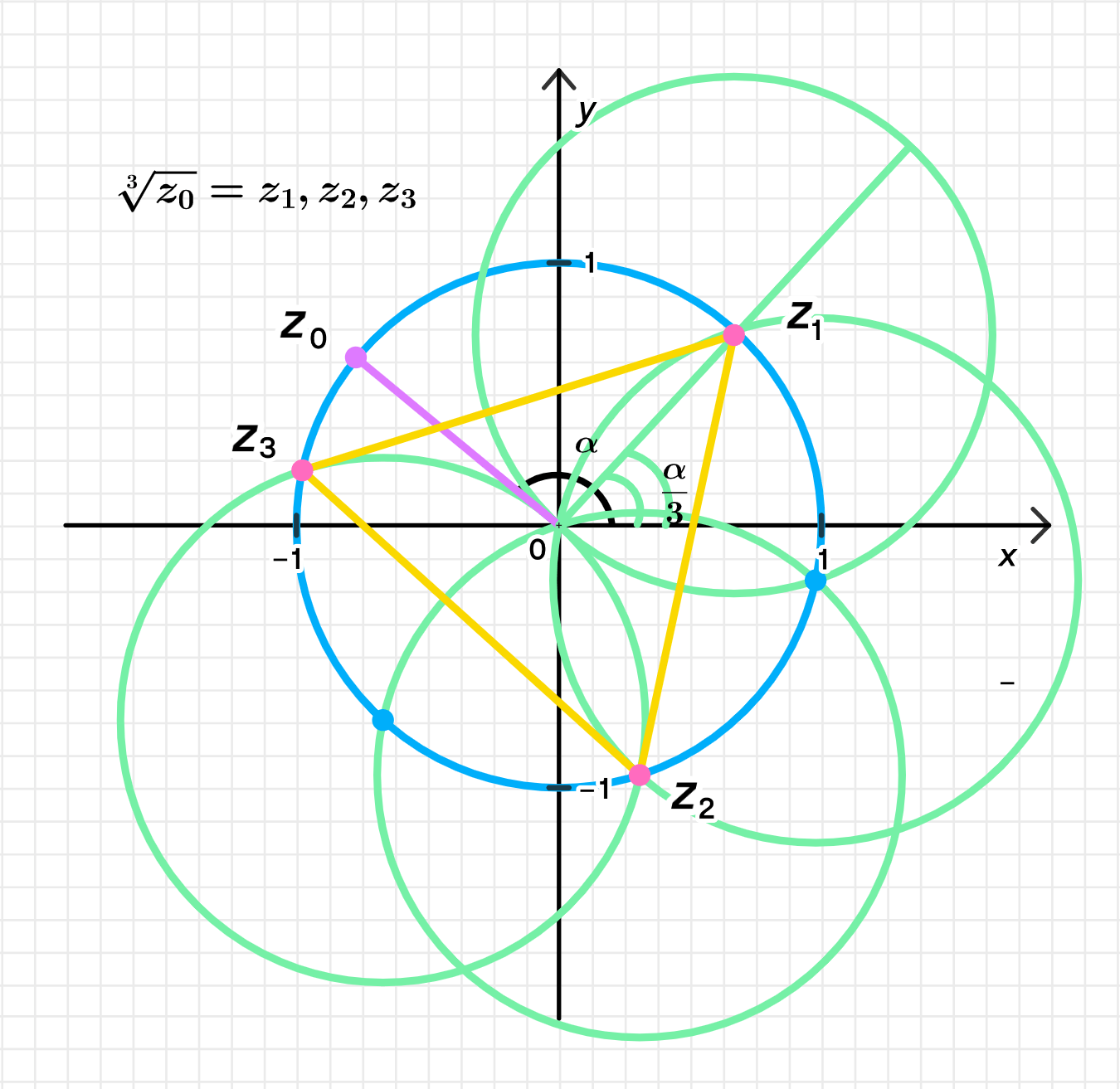ГДЗ по Алгебре 10 Класс Номер 36.21 Профильный Уровень Мордкович — Подробные Ответы

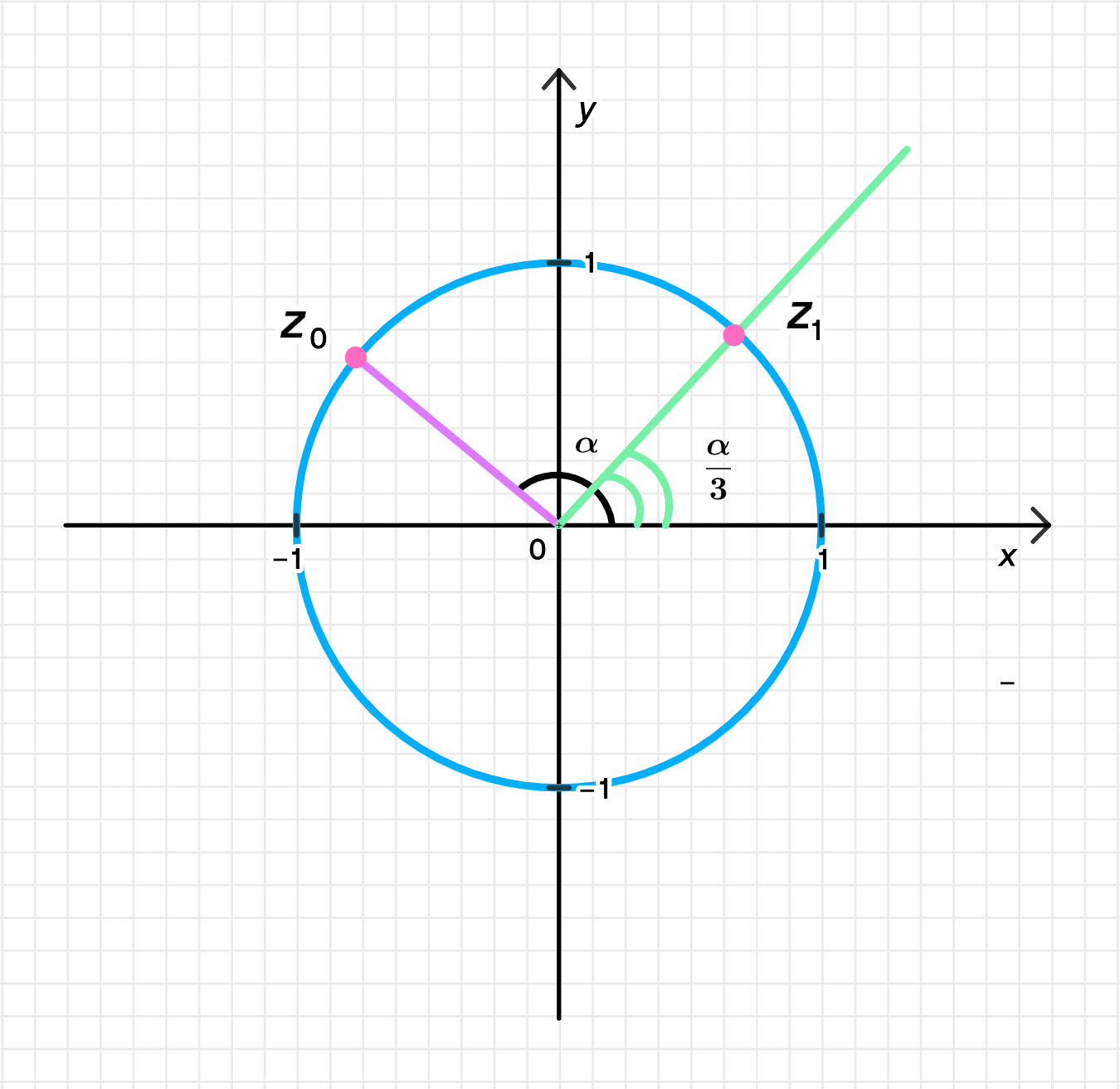
Произвольно отметьте на комплексной плоскости число $z_0$, у которого $|z_0| = 1$ и $\frac{\pi}{2} < \arg(z_0) < \pi$.

а) Изобразите корень уравнения $z^3 = z_0$, принадлежащий первой координатной четверти.

б) Изобразите корень уравнения $z^3 = z_0$, принадлежащий четвёртой координатной четверти.

в) Изобразите множество $\sqrt[3]{z_0}$.

г) Объясните, почему у уравнения $z^3 = z_0$ нет корней, расположенных в третьей четверти.

Комплексное число $z_0$, у которого $|z_0| = 1$ и $\frac{\pi}{2} < \arg(z_0) < \pi$;

Уравнение: $z^3 = z_0$, отсюда $z = \sqrt[3]{z_0}$;

а) Корень уравнения, лежащий в первой координатной четверти ($z_1$):

б) Корень уравнения, лежащий в четвертой координатной четверти ($z_3$):

в) Множество всех корней уравнения ($z_1; z_2; z_3$):

г) Уравнения нет корней, расположенных в третьей четверти, так как все его корни располагаются в вершинах равностороннего треугольника, поэтому они смещены на треть окружности, то есть $\frac{2\pi}{3}$:

$$\begin{aligned} & \frac{\pi}{2} < \arg(z_0) < \pi; \\ & \frac{\pi}{6} < \arg(z_1) < \frac{\pi}{3} — \text{первая четверть}; \\ & \frac{5\pi}{6} < \arg(z_2) < \pi — \text{вторая четверть}; \\ & \frac{3\pi}{2} < \arg(z_3) < \frac{5\pi}{3} — \text{четвертая четверть}; \end{aligned}$$

1. Исходные данные задачи

У нас есть комплексное число $z_0$, у которого выполняются следующие условия:

$$|z_0| = 1 \quad \text{и} \quad \frac{\pi}{2} < \arg(z_0) < \pi.$$

• $|z_0| = 1$ означает, что комплексное число $z_0$ находится на единичной окружности в комплексной плоскости.
• Условие $\frac{\pi}{2} < \arg(z_0) < \pi$ говорит, что аргумент числа $z_0$ лежит в пределах от $\frac{\pi}{2}$ до $\pi$, то есть $z_0$ располагается во второй координатной четверти.

Необходимо решить уравнение:

$$z^3 = z_0,$$

где $z$ — это искомое комплексное число. Сначала выразим решение этого уравнения.

2. Корни уравнения $z^3 = z_0$

Для нахождения всех корней уравнения $z^3 = z_0$ используем метод нахождения корней комплексных чисел. Поскольку $|z_0| = 1$, $z_0$ может быть записано в полярной форме как:

$$z_0 = \text{cis}(\arg(z_0)) = e^{i \arg(z_0)},$$

где $\text{cis}(\theta)$ — это сокращение для $\cos(\theta) + i \sin(\theta)$, а $\arg(z_0)$ — аргумент комплексного числа $z_0$.

Так как нам нужно найти корни уравнения $z^3 = z_0$, воспользуемся формулой для корней комплексного числа:

$$z_k = \sqrt[3]{|z_0|} \cdot \text{cis}\left(\frac{\arg(z_0) + 2k\pi}{3}\right), \quad k = 0, 1, 2.$$

Поскольку $|z_0| = 1$, то $\sqrt[3]{|z_0|} = 1$. Следовательно, корни будут иметь вид:

$$z_k = \text{cis}\left(\frac{\arg(z_0) + 2k\pi}{3}\right), \quad k = 0, 1, 2.$$

3. Описание каждого из корней

Рассмотрим каждый из корней более детально.

а) Корень, лежащий в первой координатной четверти ($z_1$)

Корень, соответствующий $k = 0$, имеет вид:

$$z_1 = \text{cis}\left(\frac{\arg(z_0)}{3}\right).$$

Поскольку $\frac{\pi}{2} < \arg(z_0) < \pi$, то:

$$\frac{\pi}{2} < \arg(z_0) < \pi \quad \Rightarrow \quad \frac{\pi}{6} < \frac{\arg(z_0)}{3} < \frac{\pi}{3}.$$

Это означает, что аргумент $z_1$ лежит в пределах от $\frac{\pi}{6}$ до $\frac{\pi}{3}$, что соответствует первой координатной четверти. Следовательно, $z_1$ лежит в первой четверти.

б) Корень, лежащий в четвертой координатной четверти ($z_3$)

Корень, соответствующий $k = 2$, имеет вид:

$$z_3 = \text{cis}\left(\frac{\arg(z_0) + 4\pi}{3}\right).$$

Для $\frac{\pi}{2} < \arg(z_0) < \pi$, это выражение для аргумента $z_3$ даёт:

$$\frac{\pi}{2} + 4\pi < \arg(z_0) + 4\pi < \pi + 4\pi \quad \Rightarrow \quad \frac{5\pi}{2} < \arg(z_0) + 4\pi < 5\pi.$$

Делим на 3:

$$\frac{5\pi}{6} < \frac{\arg(z_0) + 4\pi}{3} < \frac{5\pi}{3}.$$

Это означает, что аргумент $z_3$ лежит в пределах от $\frac{5\pi}{6}$ до $\frac{5\pi}{3}$, что соответствует четвертой координатной четверти.

в) Множество всех корней уравнения

Все три корня уравнения имеют вид:

$$z_0 = \text{cis}(\arg(z_0)), \quad z_1 = \text{cis}\left(\frac{\arg(z_0)}{3}\right), \quad z_2 = \text{cis}\left(\frac{\arg(z_0) + 2\pi}{3}\right), \quad z_3 = \text{cis}\left(\frac{\arg(z_0) + 4\pi}{3}\right).$$

Эти корни распределяются по окружности на равном расстоянии друг от друга, образуя вершины равностороннего треугольника, где углы между соседними корнями составляют $\frac{2\pi}{3}$.

г) Корни, расположенные в третьей четверти

Корни уравнения расположены в вершинах равностороннего треугольника, и все они смещены на треть окружности (на угол $\frac{2\pi}{3}$). Следовательно, нет корней, расположенных в третьей координатной четверти.

Чтобы это уточнить, приведем следующее распределение углов:

$$\begin{aligned} & \frac{\pi}{2} < \arg(z_0) < \pi; \\ & \frac{\pi}{6} < \arg(z_1) < \frac{\pi}{3} — \text{первая четверть}; \\ & \frac{5\pi}{6} < \arg(z_2) < \pi — \text{вторая четверть}; \\ & \frac{3\pi}{2} < \arg(z_3) < \frac{5\pi}{3} — \text{четвертая четверть}; \end{aligned}$$

Таким образом, все корни расположены на различных четвертях, за исключением третьей, где корней нет.