ГДЗ по Алгебре 10 Класс Номер 36.22 Профильный Уровень Мордкович — Подробные Ответы

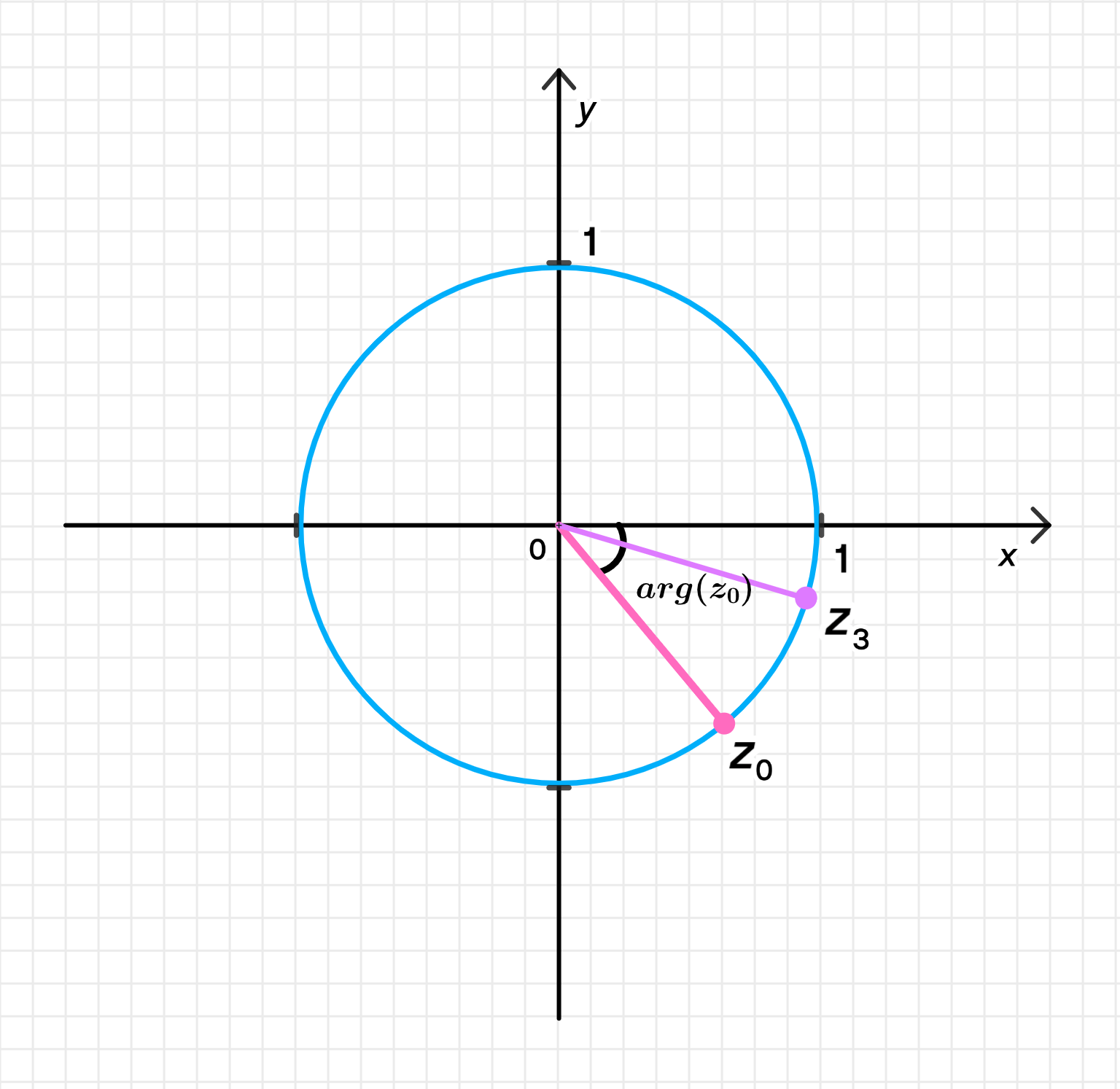
Произвольно отметьте на комплексной плоскости число $z_0$, у которого $|z_0| = 1$ и $-\frac{\pi}{2} < \arg(z_0) < 0$.

а) Изобразите корень уравнения $z^3 = z_0$, принадлежащий четвертой координатной четверти.

б) Изобразите множество $\sqrt[3]{z_0}$.

в) Объясните, почему у уравнения $z^3 = z_0$ нет корней, расположенных в первой четверти.

г) Найдите площадь треугольника с вершинами в точках из пункта б).

Комплексное число $z_0$, у которого $|z_0| = 1$ и $-\frac{\pi}{2} < \arg(z_0) < 0$;

Уравнение: $z^3 = z_0$, отсюда $z = \sqrt[3]{z_0}$;

а) Корень уравнения, лежащий в четвертой координатной четверти ($z_3$):

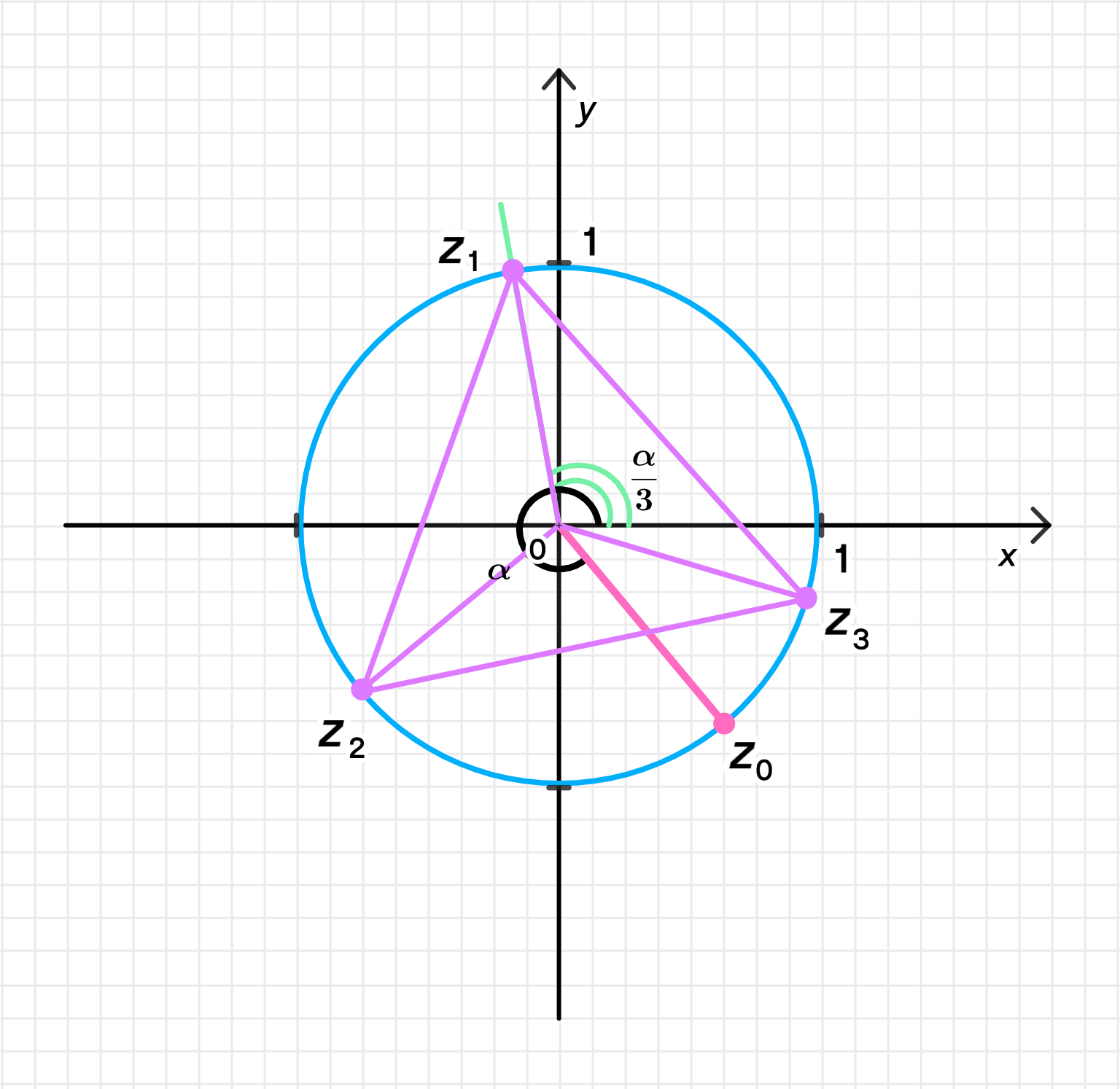
б) Множество всех корней уравнения ($z_1$; $z_2$; $z_3$):

в) У уравнения нет корней, расположенных в первой четверти, так как все его корни располагаются в вершинах равностороннего треугольника, поэтому они смещены на треть окружности, то есть $\frac{2\pi}{3}$:

$$\begin{aligned} & \frac{3\pi}{2} < \arg(z_0) < 2\pi; \\ & \frac{\pi}{2} < \arg(z_1) < \frac{2\pi}{3} — \text{вторая четверть}; \\ & \frac{7\pi}{6} < \arg(z_2) < \frac{4\pi}{3} — \text{третья четверть}; \\ & \frac{11\pi}{6} < \arg(z_3) < 2\pi — \text{четвертая четверть}; \end{aligned}$$

г) Площадь правильного треугольника, вписанного в окружность:

$$a = \sqrt{3}R = \sqrt{3};$$ $$S = \frac{\sqrt{3}}{4}a^2 = \frac{\sqrt{3}}{4} \cdot (\sqrt{3})^2 = \frac{3\sqrt{3}}{4};$$

Комплексное число $z_0$ имеет модуль $|z_0| = 1$ и аргумент $\arg(z_0)$, который лежит в интервале $-\frac{\pi}{2} < \arg(z_0) < 0$. Это означает, что $z_0$ лежит на единичной окружности, в нижней полуплоскости комплексной плоскости, между осью мнимых чисел и осью действительных чисел.

Уравнение: $z^3 = z_0$, что означает, что нужно найти кубические корни из $z_0$.

а) Корень уравнения, лежащий в четвертой координатной четверти ($z_3$):

Корни уравнения $z^3 = z_0$ можно найти с помощью формулы для корней комплексных чисел. Если число $z_0 = |z_0| (\cos \theta + i \sin \theta)$, то корни уравнения $z^3 = z_0$ имеют вид:

$$z_k = \sqrt[3]{|z_0|} \left( \cos \left( \frac{\theta + 2k\pi}{3} \right) + i \sin \left( \frac{\theta + 2k\pi}{3} \right) \right), \quad k = 0, 1, 2.$$

Так как $|z_0| = 1$, все корни будут располагаться на единичной окружности.

Рассмотрим аргументы этих корней. Аргумент $\arg(z_0)$ лежит в интервале $-\frac{\pi}{2} < \arg(z_0) < 0$, поэтому:

• $\arg(z_0) / 3$ — это начальный угол для первого корня, который лежит на некоторой полуплоскости.
• Другие два корня будут через угол $\frac{2\pi}{3}$, так как мы ищем третьи корни.

Корень $z_3$, который лежит в четвертой четверти, будет иметь аргумент $\arg(z_3) = \frac{11\pi}{6} < \arg(z_3) < 2\pi$.

Таким образом, корень $z_3$ расположен в четвертой четверти и соответствует углу от $\frac{11\pi}{6}$ до $2\pi$.

б) Множество всех корней уравнения ($z_1$, $z_2$, $z_3$):

Уравнение $z^3 = z_0$ имеет три корня. Их аргументы будут разделены на углы $\frac{2\pi}{3}$ друг от друга, то есть:

• $z_1$ — первый корень с аргументом $\frac{3\pi}{2} < \arg(z_1) < 2\pi$.
• $z_2$ — второй корень с аргументом $\frac{\pi}{2} < \arg(z_2) < \frac{2\pi}{3}$, который лежит во второй четверти.
• $z_3$ — третий корень с аргументом $\frac{7\pi}{6} < \arg(z_3) < \frac{4\pi}{3}$, который лежит в третьей четверти.
• Корень $z_3$, как мы выяснили ранее, будет расположен в четвертой четверти.

Итак, множество всех корней состоит из точек на единичной окружности, расположенных через углы $\frac{2\pi}{3}$, начиная с угла $\frac{3\pi}{2}$, что дает распределение корней на окружности.

в) У уравнения нет корней, расположенных в первой четверти:

Как мы уже выяснили, корни $z_1$, $z_2$, и $z_3$ располагаются на единичной окружности, но ни один из этих корней не попадает в первую четверть. Это связано с тем, что угол между любыми двумя корнями составляет $\frac{2\pi}{3}$, и поэтому они не могут располагаться в первой четверти.

Аргументы корней:

• Первый корень $z_1$ находится во второй четверти, угол $\frac{3\pi}{2} < \arg(z_1) < 2\pi$.
• Второй корень $z_2$ лежит в третьей четверти, угол $\frac{\pi}{2} < \arg(z_2) < \frac{2\pi}{3}$.
• Третий корень $z_3$ лежит в четвертой четверти, угол $\frac{7\pi}{6} < \arg(z_3) < \frac{4\pi}{3}$.

Все эти углы расположены вне первой четверти, и, следовательно, в первой четверти нет корней.

г) Площадь правильного треугольника, вписанного в окружность:

Корни $z_1$, $z_2$, и $z_3$ образуют равносторонний треугольник на единичной окружности.

Площадь равностороннего треугольника, вписанного в окружность радиуса $R = 1$, можно найти по формуле:

$$S = \frac{\sqrt{3}}{4} a^2,$$

где $a$ — длина стороны треугольника. Для правильного треугольника, вписанного в окружность, длина стороны равна $a = \sqrt{3} R$, где $R = 1$ — радиус окружности.

Следовательно, длина стороны $a = \sqrt{3}$, и площадь треугольника будет:

$$S = \frac{\sqrt{3}}{4} (\sqrt{3})^2 = \frac{\sqrt{3}}{4} \cdot 3 = \frac{3\sqrt{3}}{4}.$$

Таким образом, площадь треугольника равна $\frac{3\sqrt{3}}{4}$.