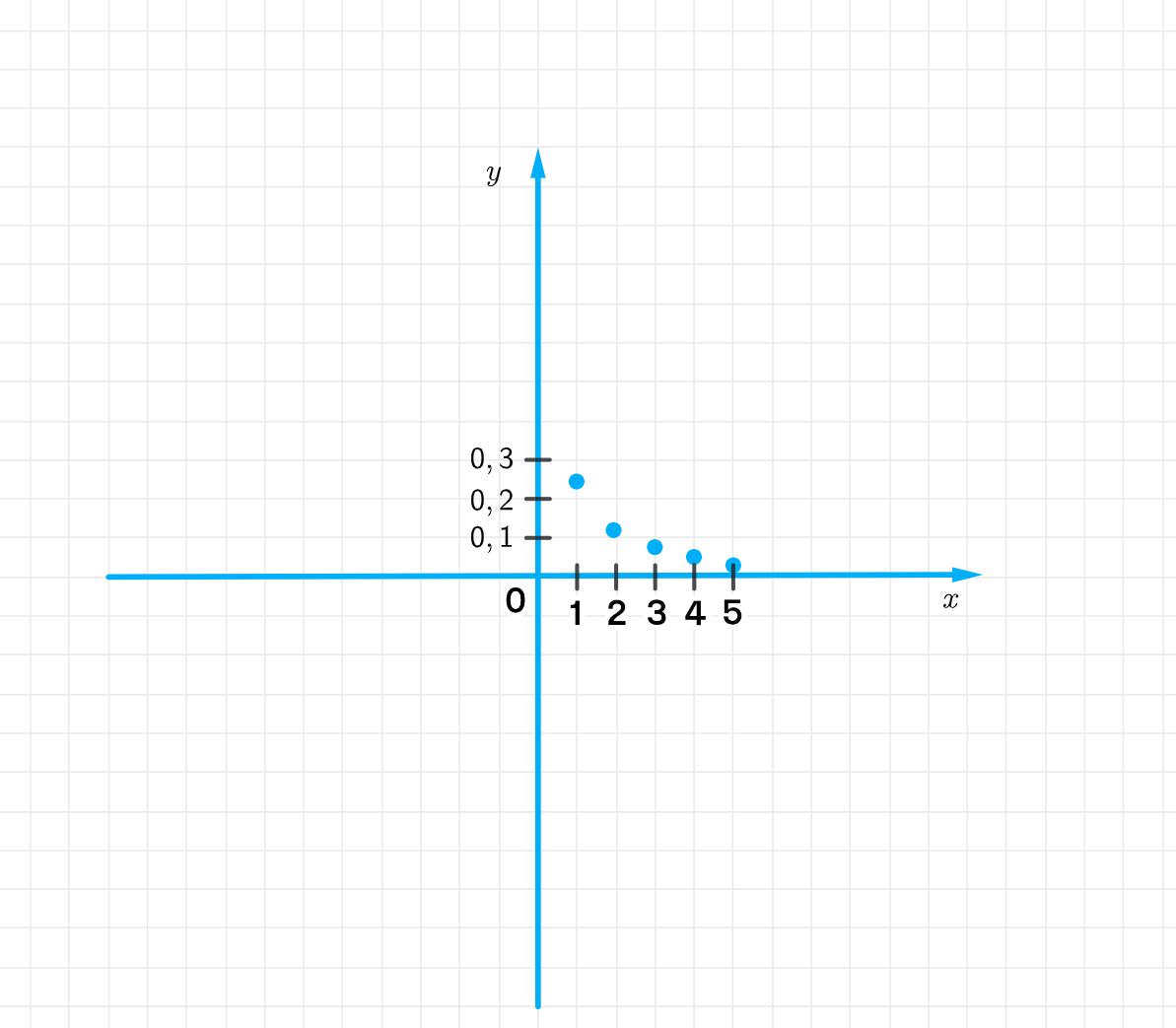Задача
Постройте график функции:
а) y = ( x + 1 ) − 2 = 1 ( x + 1 ) 2 y = (x + 1)^{-2} = \frac{1}{(x + 1)^2} x ∈ N x \in \mathbb{N}
б) y = 3 x − x 2 y = 3x — x^2 x ∈ N x \in \mathbb{N}
в) y = − 18 x + 2 y = -\frac{18}{x + 2} x ∈ N x \in \mathbb{N}
г) y = x + 3 y = \sqrt{x + 3} x ∈ N x \in \mathbb{N}
Краткий ответ:
а) y = ( x + 1 ) − 2 = 1 ( x + 1 ) 2 y = (x + 1)^{-2} = \frac{1}{(x + 1)^2} x ∈ N x \in \mathbb{N}
Значения функции:
y 1 = 1 ( 1 + 1 ) 2 = 1 2 2 = 1 4 ; y_1 = \frac{1}{(1 + 1)^2} = \frac{1}{2^2} = \frac{1}{4}; y 2 = 1 ( 2 + 1 ) 2 = 1 3 2 = 1 9 ; y_2 = \frac{1}{(2 + 1)^2} = \frac{1}{3^2} = \frac{1}{9}; y 3 = 1 ( 3 + 1 ) 2 = 1 4 2 = 1 16 ; y_3 = \frac{1}{(3 + 1)^2} = \frac{1}{4^2} = \frac{1}{16}; y 4 = 1 ( 4 + 1 ) 2 = 1 5 2 = 1 25 ; y_4 = \frac{1}{(4 + 1)^2} = \frac{1}{5^2} = \frac{1}{25}; y 5 = 1 ( 5 + 1 ) 2 = 1 6 2 = 1 36 ; y_5 = \frac{1}{(5 + 1)^2} = \frac{1}{6^2} = \frac{1}{36};
График функции:
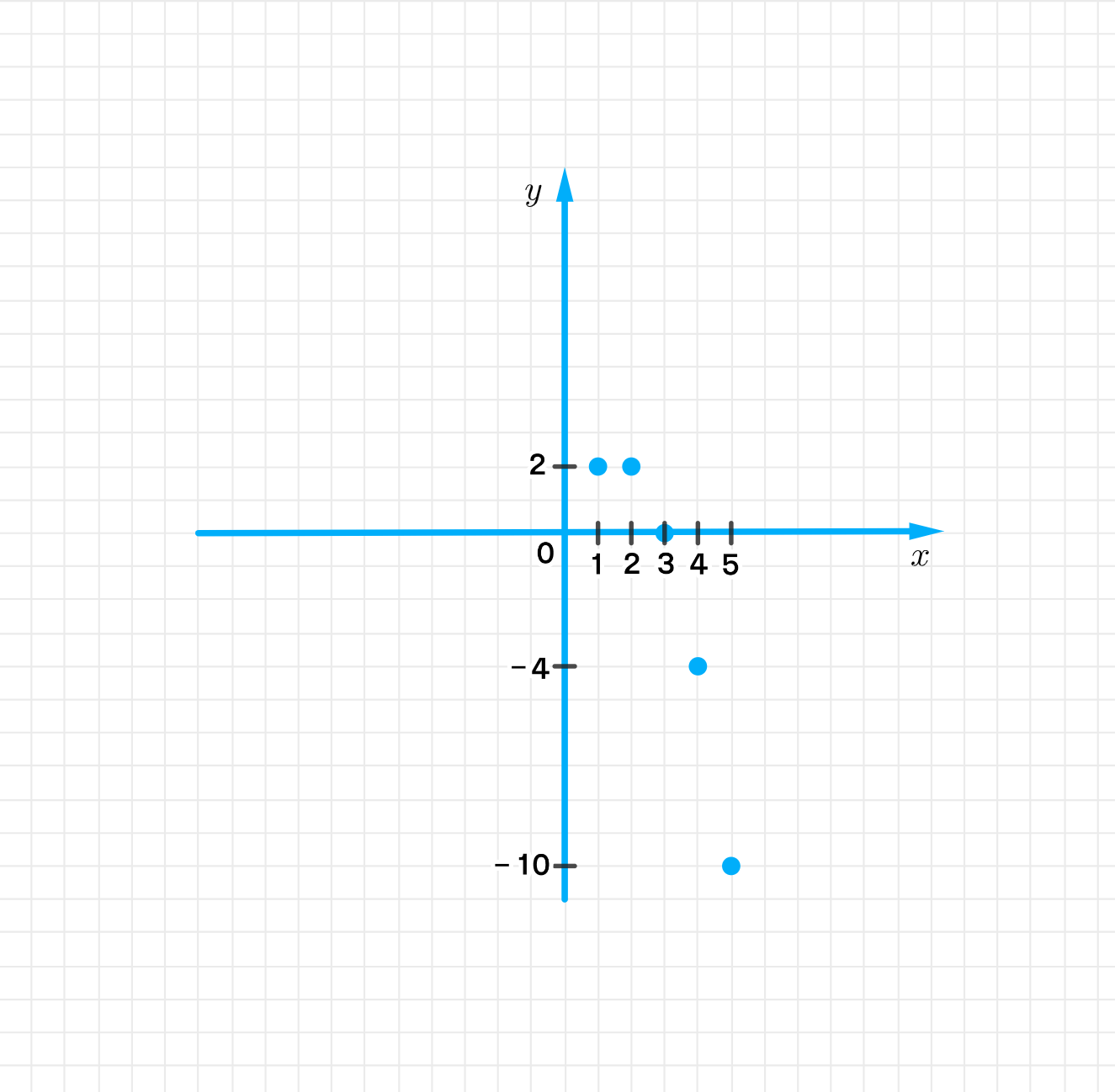
б) y = 3 x − x 2 y = 3x — x^2 x ∈ N x \in \mathbb{N}
Значения функции:
y 1 = 3 ⋅ 1 − 1 2 = 3 − 1 = 2 ; y_1 = 3 \cdot 1 — 1^2 = 3 — 1 = 2; y 2 = 3 ⋅ 2 − 2 2 = 6 − 4 = 2 ; y_2 = 3 \cdot 2 — 2^2 = 6 — 4 = 2; y 3 = 3 ⋅ 3 − 3 2 = 9 − 9 = 0 ; y_3 = 3 \cdot 3 — 3^2 = 9 — 9 = 0; y 4 = 3 ⋅ 4 − 4 2 = 12 − 16 = − 4 ; y_4 = 3 \cdot 4 — 4^2 = 12 — 16 = -4; y 5 = 3 ⋅ 5 − 5 2 = 15 − 25 = − 10 ; y_5 = 3 \cdot 5 — 5^2 = 15 — 25 = -10;
График функции:
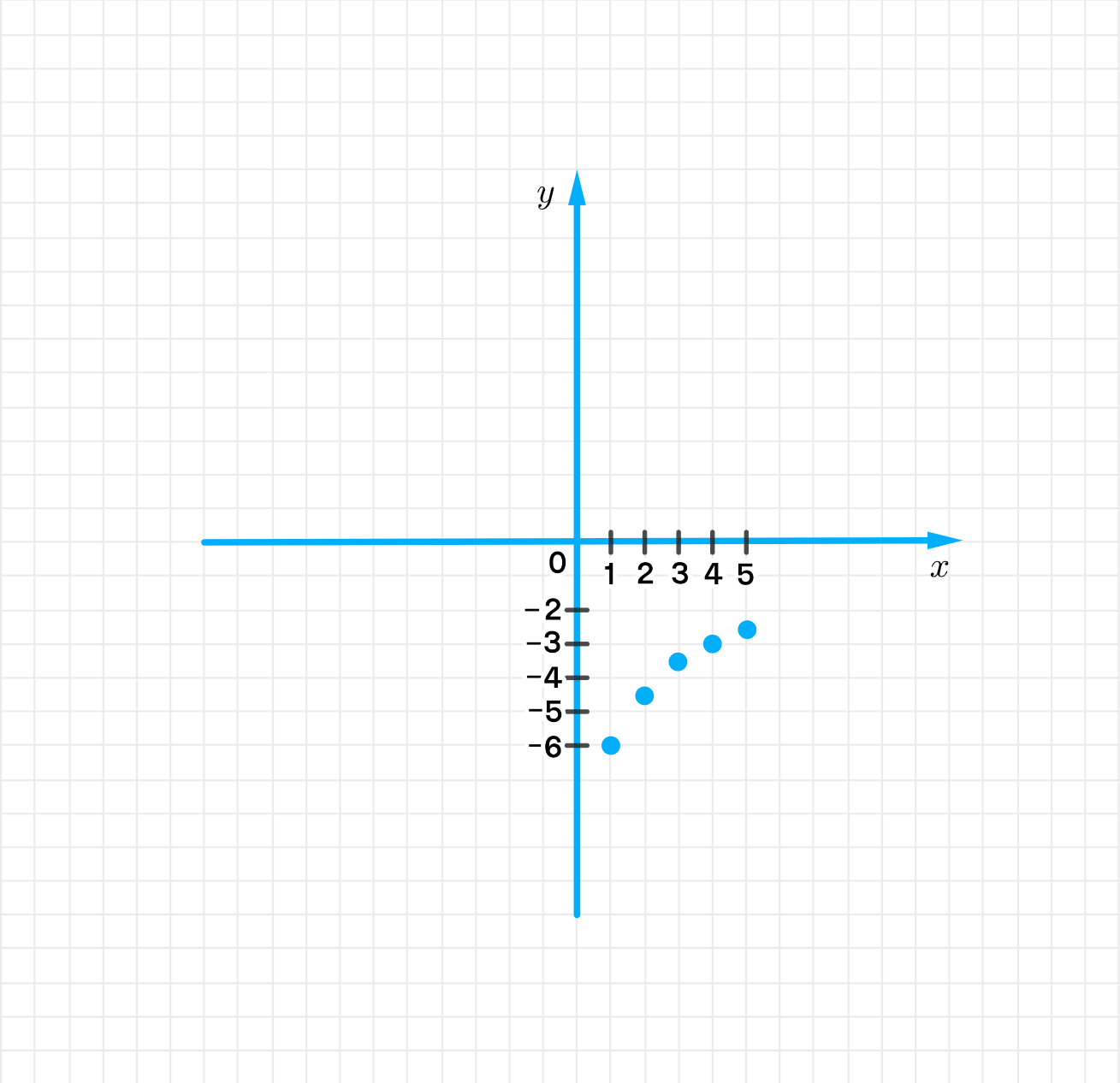
в) y = − 18 x + 2 y = -\frac{18}{x + 2} x ∈ N x \in \mathbb{N}
Значения функции:
y 1 = − 18 1 + 2 = − 18 3 = − 6 ; y_1 = -\frac{18}{1 + 2} = -\frac{18}{3} = -6; y 2 = − 18 2 + 2 = − 18 4 = − 4 , 5 ; y_2 = -\frac{18}{2 + 2} = -\frac{18}{4} = -4,5; y 3 = − 18 3 + 2 = − 18 5 = − 3 , 6 ; y_3 = -\frac{18}{3 + 2} = -\frac{18}{5} = -3,6; y 4 = − 18 4 + 2 = − 18 6 = − 3 ; y_4 = -\frac{18}{4 + 2} = -\frac{18}{6} = -3; y 5 = − 18 5 + 2 = − 18 7 = − 2 4 7 ; y_5 = -\frac{18}{5 + 2} = -\frac{18}{7} = -2\frac{4}{7};
График функции:
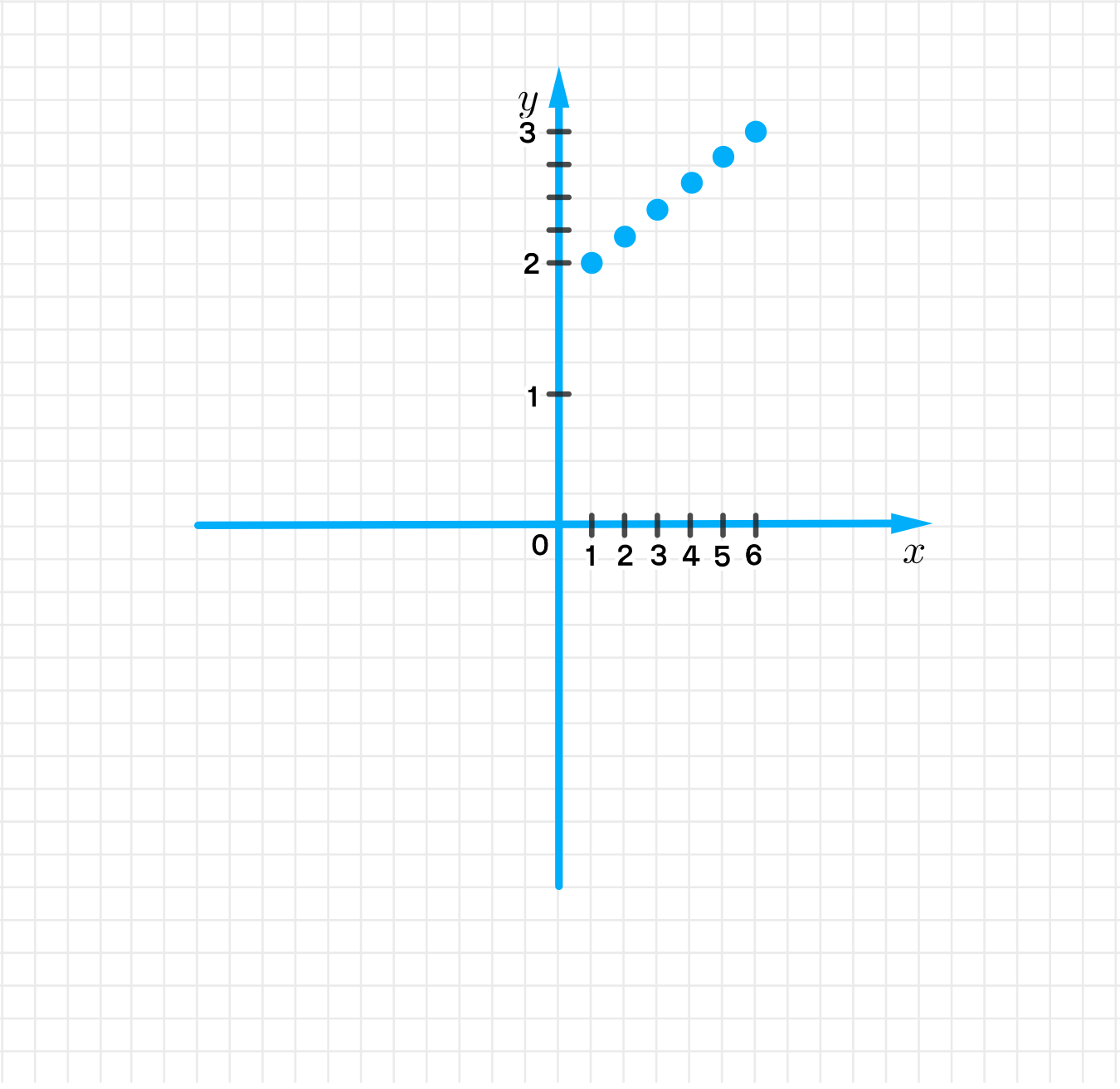
г) y = x + 3 y = \sqrt{x + 3} x ∈ N x \in \mathbb{N}
Значения функции:
y 1 = 1 + 3 = 4 = 2 ; y_1 = \sqrt{1 + 3} = \sqrt{4} = 2; y 2 = 2 + 3 = 5 ≈ 2 , 23 ; y_2 = \sqrt{2 + 3} = \sqrt{5} \approx 2,23; y 3 = 3 + 3 = 6 ≈ 2 , 44 ; y_3 = \sqrt{3 + 3} = \sqrt{6} \approx 2,44; y 4 = 4 + 3 = 7 ≈ 2 , 64 ; y_4 = \sqrt{4 + 3} = \sqrt{7} \approx 2,64; y 5 = 5 + 3 = 8 ≈ 2 , 82 ; y_5 = \sqrt{5 + 3} = \sqrt{8} \approx 2,82; y 6 = 6 + 3 = 9 = 3 ; y_6 = \sqrt{6 + 3} = \sqrt{9} = 3;
График функции:
Подробный ответ:
а) y = ( x + 1 ) − 2 = 1 ( x + 1 ) 2 y = (x + 1)^{-2} = \frac{1}{(x + 1)^2} x ∈ N x \in \mathbb{N}
1) Вычисление значений функции:
Нам дана функция y = 1 ( x + 1 ) 2 y = \frac{1}{(x + 1)^2} x = 1 , 2 , 3 , 4 , 5 x = 1, 2, 3, 4, 5
Для x = 1 x = 1 y 1 = 1 ( 1 + 1 ) 2 = 1 2 2 = 1 4 . y_1 = \frac{1}{(1 + 1)^2} = \frac{1}{2^2} = \frac{1}{4}.
Разберём шаги:
Сначала x + 1 = 1 + 1 = 2 x + 1 = 1 + 1 = 2 Затем возводим 2 в квадрат: 2 2 = 4 2^2 = 4 Далее, берём дробь: 1 4 \frac{1}{4} Для x = 2 x = 2 y 2 = 1 ( 2 + 1 ) 2 = 1 3 2 = 1 9 . y_2 = \frac{1}{(2 + 1)^2} = \frac{1}{3^2} = \frac{1}{9}.
Разберём шаги:
Сначала x + 1 = 2 + 1 = 3 x + 1 = 2 + 1 = 3 Затем возводим 3 в квадрат: 3 2 = 9 3^2 = 9 Далее, берём дробь: 1 9 \frac{1}{9} Для x = 3 x = 3 y 3 = 1 ( 3 + 1 ) 2 = 1 4 2 = 1 16 . y_3 = \frac{1}{(3 + 1)^2} = \frac{1}{4^2} = \frac{1}{16}.
Разберём шаги:
Сначала x + 1 = 3 + 1 = 4 x + 1 = 3 + 1 = 4 Затем возводим 4 в квадрат: 4 2 = 16 4^2 = 16 Далее, берём дробь: 1 16 \frac{1}{16} Для x = 4 x = 4 y 4 = 1 ( 4 + 1 ) 2 = 1 5 2 = 1 25 . y_4 = \frac{1}{(4 + 1)^2} = \frac{1}{5^2} = \frac{1}{25}.
Разберём шаги:
Сначала x + 1 = 4 + 1 = 5 x + 1 = 4 + 1 = 5 Затем возводим 5 в квадрат: 5 2 = 25 5^2 = 25 Далее, берём дробь: 1 25 \frac{1}{25} Для x = 5 x = 5 y 5 = 1 ( 5 + 1 ) 2 = 1 6 2 = 1 36 . y_5 = \frac{1}{(5 + 1)^2} = \frac{1}{6^2} = \frac{1}{36}.
Разберём шаги:
Сначала x + 1 = 5 + 1 = 6 x + 1 = 5 + 1 = 6 Затем возводим 6 в квадрат: 6 2 = 36 6^2 = 36 Далее, берём дробь: 1 36 \frac{1}{36} 2) График функции:
б) y = 3 x − x 2 y = 3x — x^2 x ∈ N x \in \mathbb{N}
1) Вычисление значений функции:
Нам дана функция y = 3 x − x 2 y = 3x — x^2 x = 1 , 2 , 3 , 4 , 5 x = 1, 2, 3, 4, 5
Для x = 1 x = 1 y 1 = 3 ⋅ 1 − 1 2 = 3 − 1 = 2. y_1 = 3 \cdot 1 — 1^2 = 3 — 1 = 2.
Разберём шаги:
Сначала умножаем 3 на 1: 3 ⋅ 1 = 3 3 \cdot 1 = 3 Затем вычитаем 1 2 = 1 1^2 = 1 3 − 1 = 2 3 — 1 = 2 Для x = 2 x = 2 y 2 = 3 ⋅ 2 − 2 2 = 6 − 4 = 2. y_2 = 3 \cdot 2 — 2^2 = 6 — 4 = 2.
Разберём шаги:
Сначала умножаем 3 на 2: 3 ⋅ 2 = 6 3 \cdot 2 = 6 Затем вычитаем 2 2 = 4 2^2 = 4 6 − 4 = 2 6 — 4 = 2 Для x = 3 x = 3 y 3 = 3 ⋅ 3 − 3 2 = 9 − 9 = 0. y_3 = 3 \cdot 3 — 3^2 = 9 — 9 = 0.
Разберём шаги:
Сначала умножаем 3 на 3: 3 ⋅ 3 = 9 3 \cdot 3 = 9 Затем вычитаем 3 2 = 9 3^2 = 9 9 − 9 = 0 9 — 9 = 0 Для x = 4 x = 4 y 4 = 3 ⋅ 4 − 4 2 = 12 − 16 = − 4. y_4 = 3 \cdot 4 — 4^2 = 12 — 16 = -4.
Разберём шаги:
Сначала умножаем 3 на 4: 3 ⋅ 4 = 12 3 \cdot 4 = 12 Затем вычитаем 4 2 = 16 4^2 = 16 12 − 16 = − 4 12 — 16 = -4 Для x = 5 x = 5 y 5 = 3 ⋅ 5 − 5 2 = 15 − 25 = − 10. y_5 = 3 \cdot 5 — 5^2 = 15 — 25 = -10.
Разберём шаги:
Сначала умножаем 3 на 5: 3 ⋅ 5 = 15 3 \cdot 5 = 15 Затем вычитаем 5 2 = 25 5^2 = 25 15 − 25 = − 10 15 — 25 = -10 2) График функции:
в) y = − 18 x + 2 y = -\frac{18}{x + 2} x ∈ N x \in \mathbb{N}
1) Вычисление значений функции:
Нам дана функция y = − 18 x + 2 y = -\frac{18}{x + 2} x = 1 , 2 , 3 , 4 , 5 x = 1, 2, 3, 4, 5
Для x = 1 x = 1 y 1 = − 18 1 + 2 = − 18 3 = − 6. y_1 = -\frac{18}{1 + 2} = -\frac{18}{3} = -6.
Разберём шаги:
Сначала x + 2 = 1 + 2 = 3 x + 2 = 1 + 2 = 3 Затем делим 18 на 3: 18 3 = 6 \frac{18}{3} = 6 Берём отрицательное значение: − 6 -6 Для x = 2 x = 2 y 2 = − 18 2 + 2 = − 18 4 = − 4 , 5. y_2 = -\frac{18}{2 + 2} = -\frac{18}{4} = -4,5.
Разберём шаги:
Сначала x + 2 = 2 + 2 = 4 x + 2 = 2 + 2 = 4 Затем делим 18 на 4: 18 4 = 4 , 5 \frac{18}{4} = 4,5 Берём отрицательное значение: − 4 , 5 -4,5 Для x = 3 x = 3 y 3 = − 18 3 + 2 = − 18 5 = − 3 , 6. y_3 = -\frac{18}{3 + 2} = -\frac{18}{5} = -3,6.
Разберём шаги:
Сначала x + 2 = 3 + 2 = 5 x + 2 = 3 + 2 = 5 Затем делим 18 на 5: 18 5 = 3 , 6 \frac{18}{5} = 3,6 Берём отрицательное значение: − 3 , 6 -3,6 Для x = 4 x = 4 y 4 = − 18 4 + 2 = − 18 6 = − 3. y_4 = -\frac{18}{4 + 2} = -\frac{18}{6} = -3.
Разберём шаги:
Сначала x + 2 = 4 + 2 = 6 x + 2 = 4 + 2 = 6 Затем делим 18 на 6: 18 6 = 3 \frac{18}{6} = 3 Берём отрицательное значение: − 3 -3 Для x = 5 x = 5 y 5 = − 18 5 + 2 = − 18 7 = − 2 4 7 . y_5 = -\frac{18}{5 + 2} = -\frac{18}{7} = -2\frac{4}{7}.
Разберём шаги:
Сначала x + 2 = 5 + 2 = 7 x + 2 = 5 + 2 = 7 Затем делим 18 на 7: 18 7 ≈ 2 , 5714 \frac{18}{7} \approx 2,5714 2 4 7 2\frac{4}{7} 2) График функции:
г) y = x + 3 y = \sqrt{x + 3} x ∈ N x \in \mathbb{N}
1) Вычисление значений функции:
Нам дана функция y = x + 3 y = \sqrt{x + 3} x = 1 , 2 , 3 , 4 , 5 , 6 x = 1, 2, 3, 4, 5, 6
Для x = 1 x = 1 y 1 = 1 + 3 = 4 = 2. y_1 = \sqrt{1 + 3} = \sqrt{4} = 2.
Разберём шаги:
Сначала x + 3 = 1 + 3 = 4 x + 3 = 1 + 3 = 4 Затем извлекаем квадратный корень из 4: 4 = 2 \sqrt{4} = 2 Для x = 2 x = 2 y 2 = 2 + 3 = 5 ≈ 2 , 23. y_2 = \sqrt{2 + 3} = \sqrt{5} \approx 2,23.
Разберём шаги:
Сначала x + 3 = 2 + 3 = 5 x + 3 = 2 + 3 = 5 Затем извлекаем квадратный корень из 5: 5 ≈ 2 , 23 \sqrt{5} \approx 2,23 Для x = 3 x = 3 y 3 = 3 + 3 = 6 ≈ 2 , 44. y_3 = \sqrt{3 + 3} = \sqrt{6} \approx 2,44.
Разберём шаги:
Сначала x + 3 = 3 + 3 = 6 x + 3 = 3 + 3 = 6 Затем извлекаем квадратный корень из 6: 6 ≈ 2 , 44 \sqrt{6} \approx 2,44 Для x = 4 x = 4 y 4 = 4 + 3 = 7 ≈ 2 , 64. y_4 = \sqrt{4 + 3} = \sqrt{7} \approx 2,64.
Разберём шаги:
Сначала x + 3 = 4 + 3 = 7 x + 3 = 4 + 3 = 7 Затем извлекаем квадратный корень из 7: 7 ≈ 2 , 64 \sqrt{7} \approx 2,64 Для x = 5 x = 5 y 5 = 5 + 3 = 8 ≈ 2 , 82. y_5 = \sqrt{5 + 3} = \sqrt{8} \approx 2,82.
Разберём шаги:
Сначала x + 3 = 5 + 3 = 8 x + 3 = 5 + 3 = 8 Затем извлекаем квадратный корень из 8: 8 ≈ 2 , 82 \sqrt{8} \approx 2,82 Для x = 6 x = 6 y 6 = 6 + 3 = 9 = 3. y_6 = \sqrt{6 + 3} = \sqrt{9} = 3.
Разберём шаги:
Сначала x + 3 = 6 + 3 = 9 x + 3 = 6 + 3 = 9 Затем извлекаем квадратный корень из 9: 9 = 3 \sqrt{9} = 3 2) График функции: