ГДЗ по Алгебре 10 Класс Номер 39.10 Профильный Уровень Мордкович — Подробные Ответы

Постройте график непрерывной на $(-∞; +∞)$ функции $y = f(x)$, обладающей следующими свойствами:

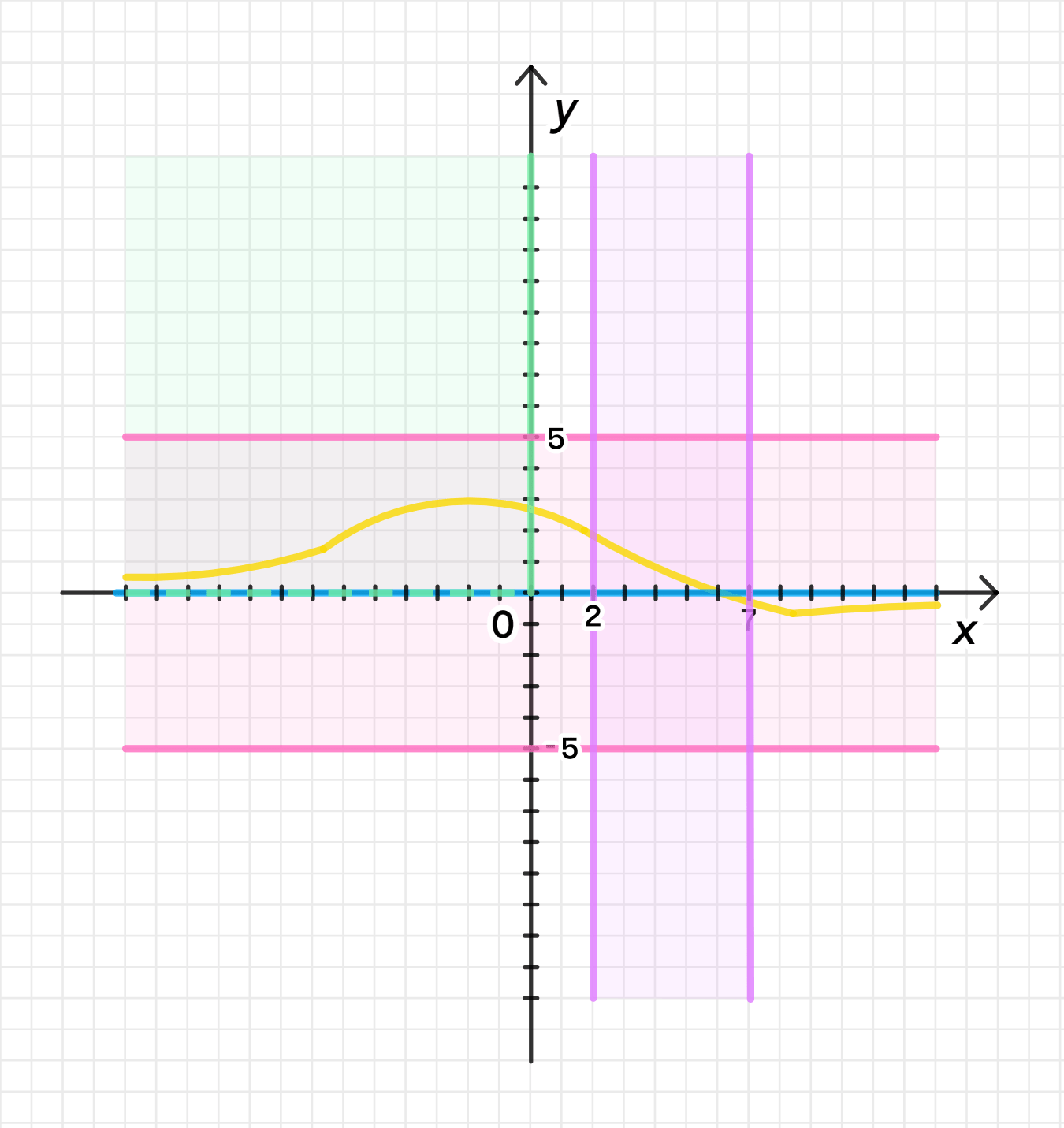
а) $\lim_{x \to ∞} f(x) = 0$; $f(x) > 0$ на $(-∞; 0)$; $E(f) = [-5; 5]$, функция убывает на $[2; 7]$;

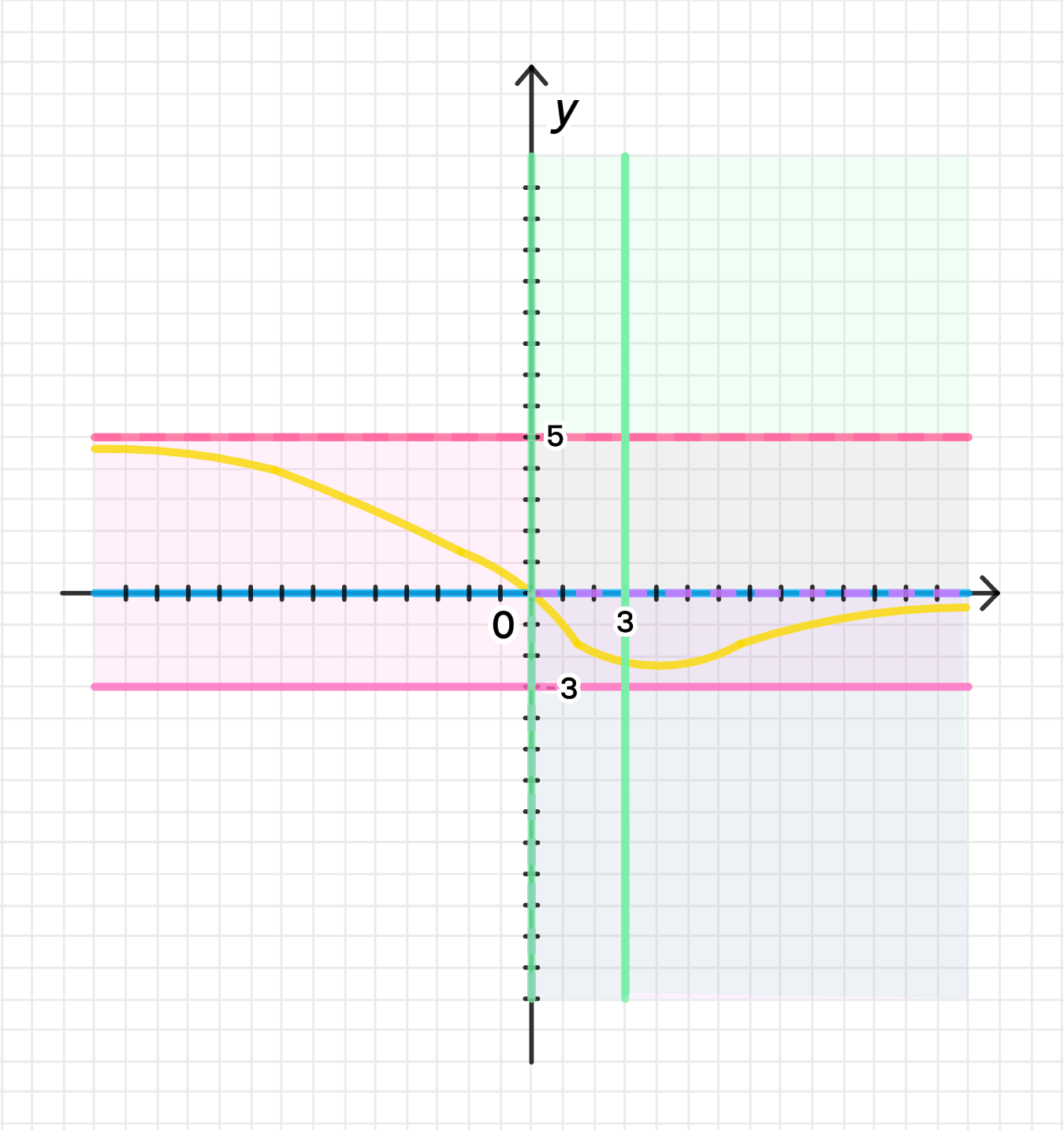
б) $\lim_{x \to -∞} f(x) = 5$, $\lim_{x \to ∞} f(x) = 0$, $E(f) = [-3; 5)$, $f(x) < 0$ на $(0; +∞)$, функция возрастает на $[3; +∞)$ и убывает на $[0; 3]$.

а) Свойства непрерывной функции:

$$\lim_{x \to \infty} f(x) = 0;$$ $$f(x) > 0 \text{ на } (-\infty; 0);$$ $$E(f) = [-5; 5];$$ $$\text{Убывает на } [2; 7];$$

б) Свойства непрерывной функции:

$$\lim_{x \to -\infty} f(x) = 5;$$ $$\lim_{x \to \infty} f(x) = 0;$$ $$E(f) = [-3; 5);$$ $$f(x) < 0 \text{ на } (0; +\infty);$$ $$\text{Возрастает на } [3; +\infty);$$ $$\text{Убывает на }[0;3];$$

$$\text{Убывает на } [0; 3];$$

а)

Дано:

• $\lim_{x \to \infty} f(x) = 0$
• $f(x) > 0 \text{ на } (-\infty; 0)$
• $E(f) = [-5; 5]$
• Функция убывает на $[2; 7]$

Подбор функции:

Предел при $x \to \infty$:

$$\lim_{x \to \infty} f(x) = 0$$

Это означает, что функция стремится к нулю при $x \to \infty$, то есть на больших значениях $x$ функция будет близка к 0. В качестве примера можно выбрать функцию:

$$f(x) = \frac{5}{x^2 + 1}$$

Когда $x$ увеличивается, функция будет стремиться к нулю, так как знаменатель растет быстрее числителя.

Функция больше нуля на $(-∞; 0)$:
Чтобы функция была положительной на интервале $(-∞; 0)$, мы можем использовать дробь с положительным числителем и знаменателем. В данном случае функция $\frac{5}{x^2 + 1}$ положительна на всем интервале, так как знаменатель всегда положителен для любого значения $x$, и функция определена на всей числовой прямой.

Образ $E(f) = [-5; 5]$:
Это ограничение означает, что значения функции $f(x)$ должны находиться в пределах от -5 до 5. Функция $\frac{5}{x^2 + 1}$ будет варьироваться от 0 до 5, то есть она подходит по этому условию.

Функция убывает на $[2; 7]$:
Чтобы функция убывала на интервале $[2; 7]$, необходимо, чтобы её производная была отрицательной на этом интервале. Для функции $\frac{5}{x^2 + 1}$ производная имеет вид:

$$f'(x) = -\frac{10x}{(x^2 + 1)^2}$$

Это выражение всегда будет отрицательным при $x > 0$, то есть функция убывает на правой части числовой прямой, в том числе на интервале $[2; 7]$.

Построение графика для условия (а):

• Функция будет стремиться к 0 при $x \to \infty$.
• Она будет положительной для всех $x < 0$, и постепенно уменьшаться, приближаясь к нулю.
• На интервале $[2; 7]$ функция будет убывать, как этого требует условие.

б)

Дано:

• $\lim_{x \to -\infty} f(x) = 5$
• $\lim_{x \to \infty} f(x) = 0$
• $E(f) = [-3; 5)$
• $f(x) < 0 \text{ на } (0; +\infty)$
• Функция возрастает на $[3; +\infty)$
• Функция убывает на $[0; 3]$

Подбор функции:

Предел при $x \to -\infty$:

$$\lim_{x \to -\infty} f(x) = 5$$

Это означает, что при $x \to -\infty$ функция должна стремиться к 5. В качестве подходящей функции можно выбрать:

$$f(x) = 5 — \frac{1}{x^2 + 1}$$

При $x \to -\infty$, $\frac{1}{x^2 + 1} \to 0$, и функция $f(x)$ будет стремиться к 5.

Предел при $x \to \infty$:

$$\lim_{x \to \infty} f(x) = 0$$

На больших значениях $x$ функция должна стремиться к 0. Функция $\frac{1}{x^2 + 1}$ имеет тот же предел при $x \to \infty$, и её можно использовать в качестве части функции.

Образ $E(f) = [-3; 5)$:
Это ограничение означает, что значения функции $f(x)$ должны находиться в пределах от -3 до 5. Функция $\frac{1}{x^2 + 1}$ будет варьироваться от 0 до 1, и если мы вычтем её из 5, то значения функции будут в пределах от 4 до 5 при $x \to -\infty$ и стремиться к 0 при $x \to \infty$.

Функция отрицательна на $(0; +\infty)$:
Чтобы функция была отрицательной на интервале $(0; +\infty)$, нужно добавить знак минус перед дробью, например:

$$f(x) = -\frac{1}{x^2 + 1}$$

Эта функция будет отрицательной для всех $x > 0$.

Функция возрастает на $[3; +\infty)$:
Чтобы функция возрастала на интервале $[3; +\infty)$, нужно, чтобы её производная была положительной на этом интервале. В функции $-\frac{1}{x^2 + 1}$ производная будет положительной на интервале, начинающемся с $x = 3$ и продолжаясь дальше.

Функция убывает на $[0; 3]$:
Функция должна убывать на интервале $[0; 3]$, что также обеспечивается её производной, которая будет отрицательной на этом интервале.

Построение графика для условия (б):

• Функция будет стремиться к 5 при $x \to -\infty$ и к 0 при $x \to \infty$.
• Она будет отрицательной для $x > 0$.
• На интервале $[0; 3]$ функция будет убывать, а на интервале $[3; +\infty)$ она будет возрастать.

Обобщение шагов для построения графиков:

1. Выбор функции: Для каждого из условий выберите функцию, которая соответствует заданным ограничениям.
2. Вычисление значений функции: Для различных значений $x$ вычисляйте значения функции $f(x)$, чтобы увидеть, как она ведет себя в разных областях числовой оси.
3. Построение графика: На основе вычисленных значений строьте график функции, учитывая её асимптоты, интервалы возрастания и убывания, а также ограничения на диапазон значений.
4. Анализ поведения функции: Обратите внимание на то, как функция ведет себя при $x \to -\infty$ и $x \to \infty$, а также на участках, где она убывает или возрастает.