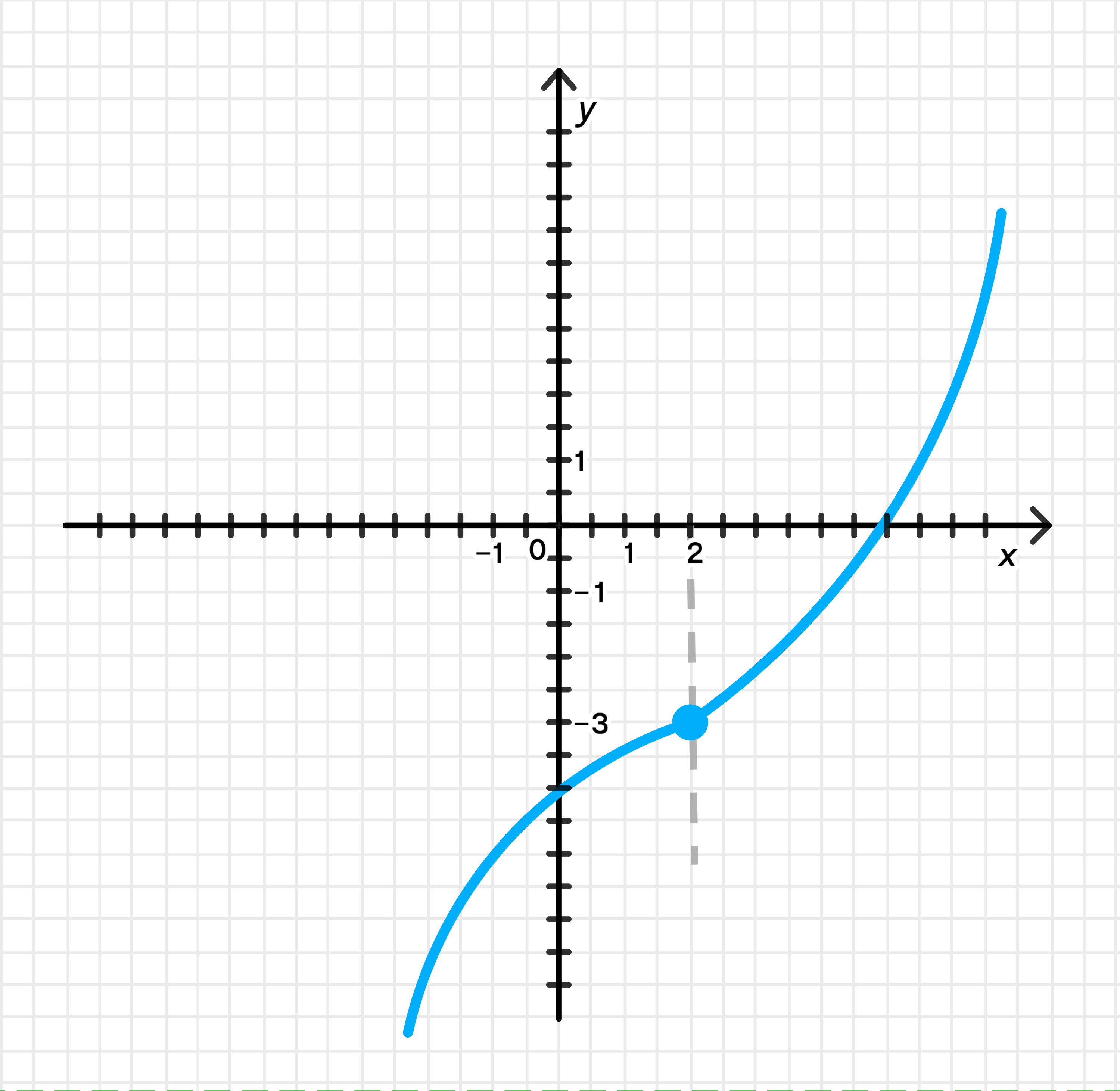ГДЗ по Алгебре 10 Класс Номер 39.19 Профильный Уровень Мордкович — Подробные Ответы

Постройте график какой-нибудь функции у = g(x), обладающей заданным свойством:

a) $\lim_{x \to -1} f(x) = 2$

б) $\lim_{x \to 2} f(x) = -3$

в) $\lim_{x \to -7} f(x) = -4$

г) $\lim_{x \to 5} f(x) = 3,5$

a) $\lim_{x \to -1} f(x) = 2$:

б) $\lim_{x \to 2} f(x) = -3$:

в) $\lim_{x \to -7} f(x) = -4$:

г) $\lim_{x \to 5} f(x) = 3,5$:

a): $\lim_{x \to -1} f(x) = 2$

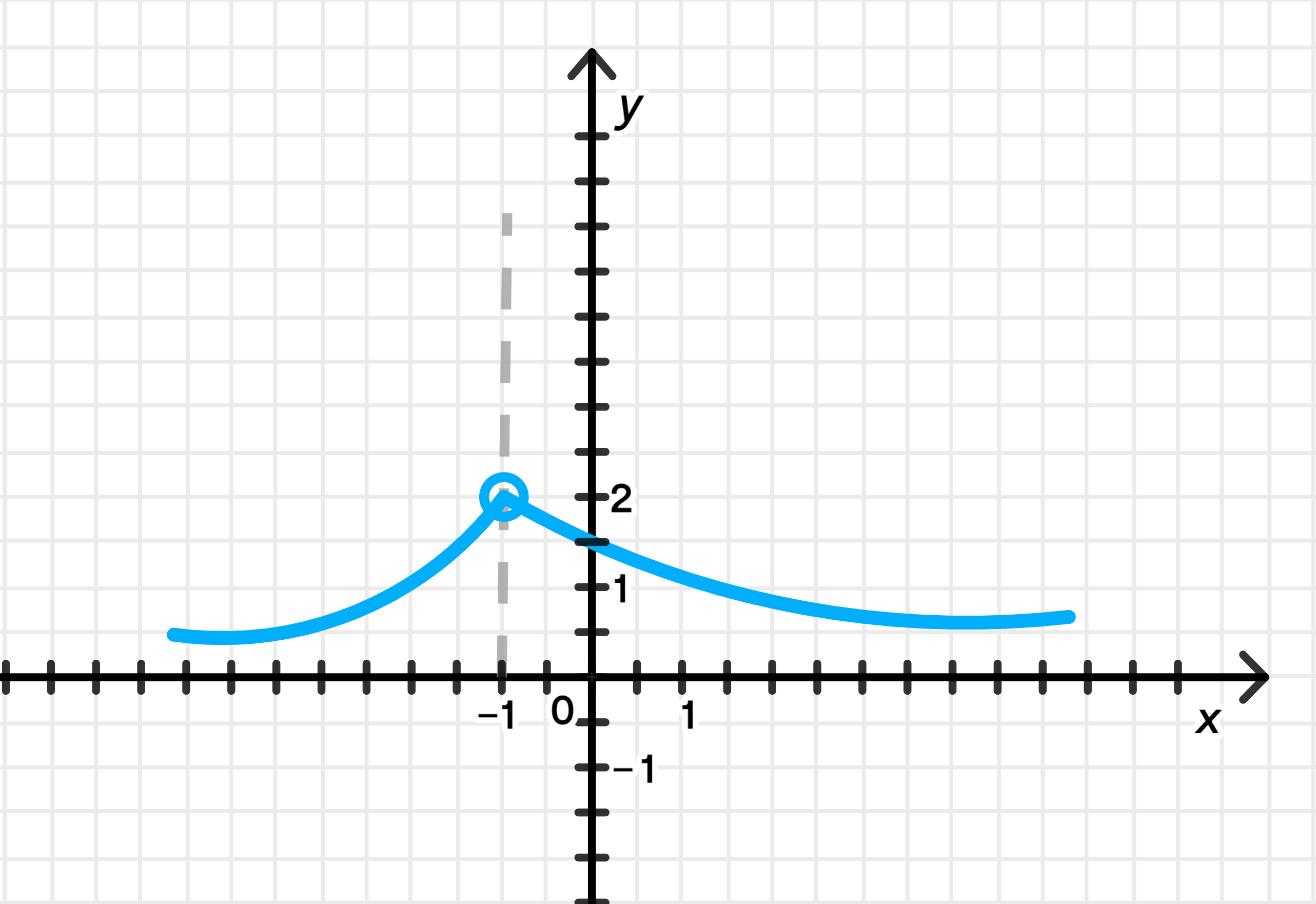
Условие: Нужно построить график функции, которая имеет предел при $x \to -1$, равный 2.

1. Выбор функции:

Для примера, возьмём функцию $f(x) = \frac{x + 1}{x^2 + 1}$. Эта функция имеет вид дроби, где числитель $x + 1$ стремится к 0, а знаменатель $x^2 + 1$ всегда положительный и не обращается в ноль, так как $x^2 + 1 \geq 1$.

2. График:

• При $x = -1$ числитель стремится к нулю ($f(-1) = \frac{-1 + 1}{(-1)^2 + 1} = 0$), что означает, что в точке $x = -1$ функция будет пересекать ось $y$ на уровне 2.
• Горизонтальная асимптота будет на уровне $y = 0$, поскольку при $x \to \infty$, функция будет стремиться к нулю.

Чтобы построить график, нужно нарисовать функцию, отметив точку пересечения с осью $x$ и горизонтальные асимптоты. Функция будет гладко подходить к точке $(-1, 2)$, стремясь к значению 2.

3. Объяснение:

Функция сходится к значению 2 при $x \to -1$, что и подтверждается на графике.

б): $\lim_{x \to 2} f(x) = -3$

Условие: Нужно построить график функции, у которой предел при $x \to 2$ равен -3.

1. Выбор функции:

Рассмотрим функцию $f(x) = \frac{2x — 7}{x — 2}$. Эта функция будет иметь разрыв в точке $x = 2$, так как в знаменателе будет стоять $x — 2$.

2. График:

• При $x = 2$, лимит функции будет стремиться к -3, так как:

  $$\lim_{x \to 2} \frac{2x — 7}{x — 2} = \lim_{x \to 2} \frac{4 — 7}{2 — 2} = -3.$$

• Вертикальная асимптота будет в точке $x = 2$, так как в знаменателе есть выражение $x — 2$.

Чтобы построить график, нужно нарисовать вертикальную асимптоту в точке $x = 2$ и показать, как функция стремится к -3 при подходе к этой точке.

3. Объяснение:

При $x \to 2$ график функции будет стремиться к $y = -3$, но не будет пересекать эту точку, поскольку есть разрыв.

в): $\lim_{x \to -7} f(x) = -4$

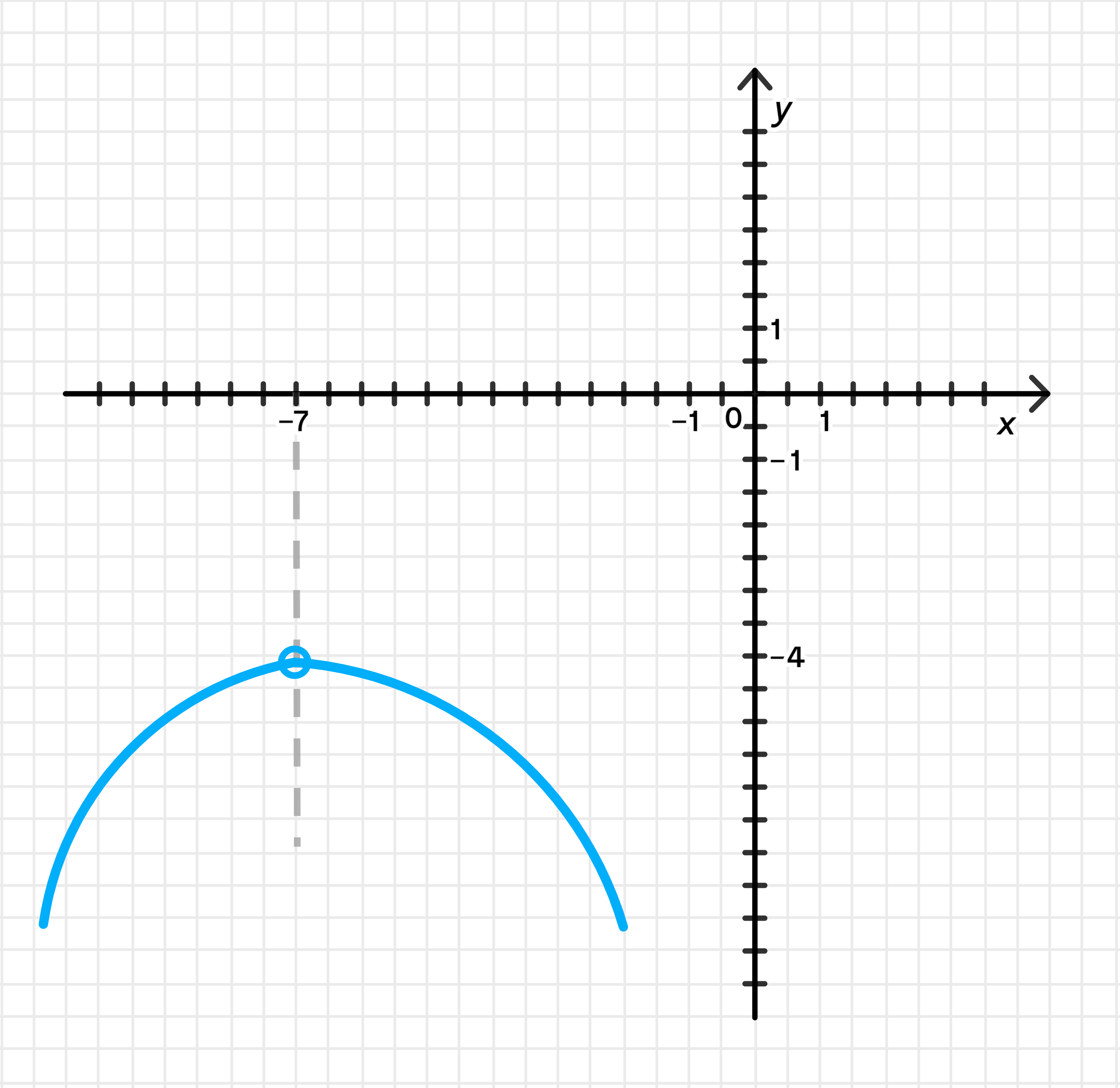
Условие: Нужно построить график функции, у которой предел при $x \to -7$ равен -4.

1. Выбор функции:

Для примера можно взять функцию вида:

$$f(x) = \frac{5x + 28}{x + 7}$$

• При $x = -7$, числитель будет равен $5(-7) + 28 = -35 + 28 = -7$, а знаменатель равен 0, что указывает на вертикальную асимптоту в точке $x = -7$.
• График будет стремиться к $y = -4$, так как предел $\lim_{x \to -7} f(x) = -4$.

2. График:

• Нарисовать вертикальную асимптоту в точке $x = -7$.
• Показать, как функция приближается к $y = -4$ при подходе к этой точке.

3. Объяснение:

При $x \to -7$ функция стремится к значению -4, что будет подтверждаться на графике как предел функции с обеих сторон вертикальной асимптоты.

г): $\lim_{x \to 5} f(x) = 3,5$

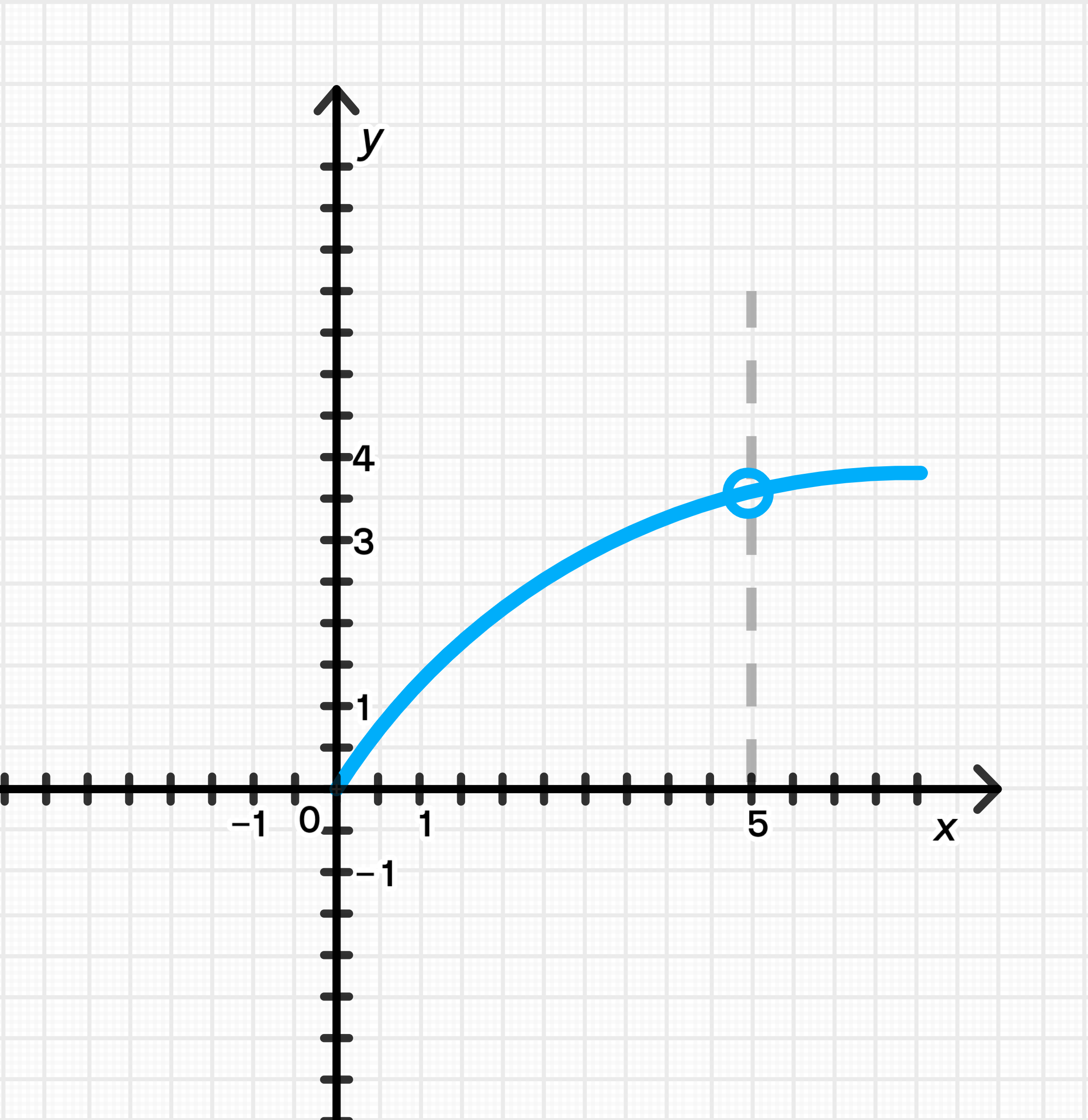
Условие: Нужно построить график функции, у которой предел при $x \to 5$ равен 3,5.

1. Выбор функции:

Рассмотрим функцию:

$$f(x) = \frac{3x + 2}{x — 5}$$

• Эта функция имеет разрыв в точке $x = 5$, так как в знаменателе стоит $x — 5$.
• При подходе к $x = 5$, предел функции будет равен 3,5.

2. График:

• Нарисовать вертикальную асимптоту в точке $x = 5$.
• Показать, как график приближается к значению 3,5 при подходе к этой точке.

3. Объяснение:

При $x \to 5$ функция будет стремиться к значению 3,5, и это будет видно на графике как приближение к горизонтальной линии $y = 3,5$.