Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 39.20 Профильный Уровень Мордкович — Подробные Ответы
Постройте график какой-нибудь функции у = f(x), обладающей заданными свойствами:
а) и
б) и
в) и не существует
г) и
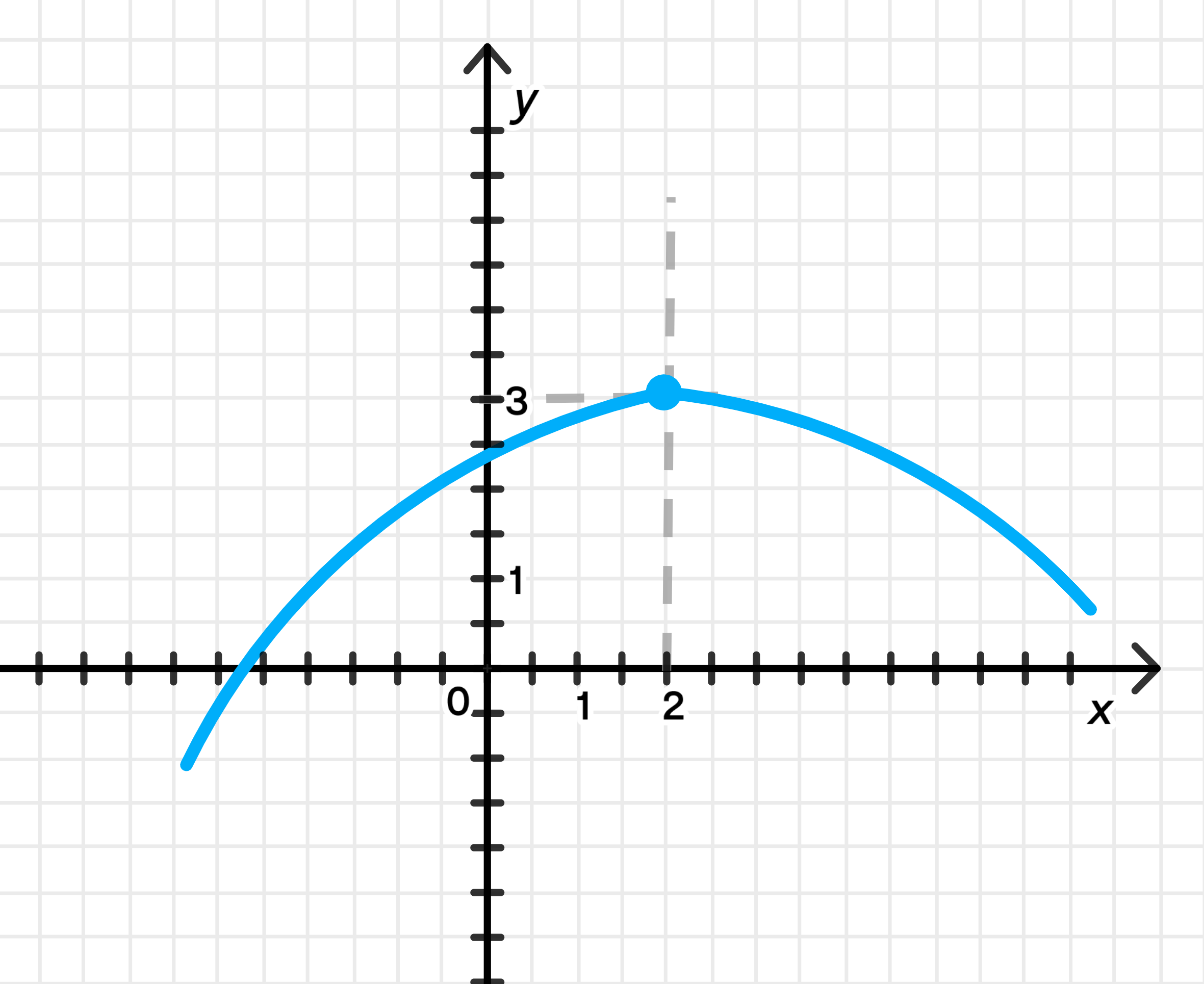
а) и
Условие: График функции должен показывать, что при функция стремится к значению 3, и при этом сама функция в точке принимает значение 3.
1. Пояснение:
- Предел функции при равен 3, что означает, что как слева, так и справа от точки функция должна стремиться к значению 3.
- Кроме того, в точке сама функция принимает значение . Это означает, что функция не имеет разрыва или скачка в этой точке, а плавно проходит через неё.
- На графике это будет выглядеть как плавное продолжение кривой, с точкой на оси в точке .
2. Как построить график:
- Отметьте точку на графике.
- Построьте плавную кривую, которая стремится к этой точке как слева, так и справа от неё.
- В точке функция пересекает ось , и кривизна графика будет непрерывной, без разрывов или скачков.
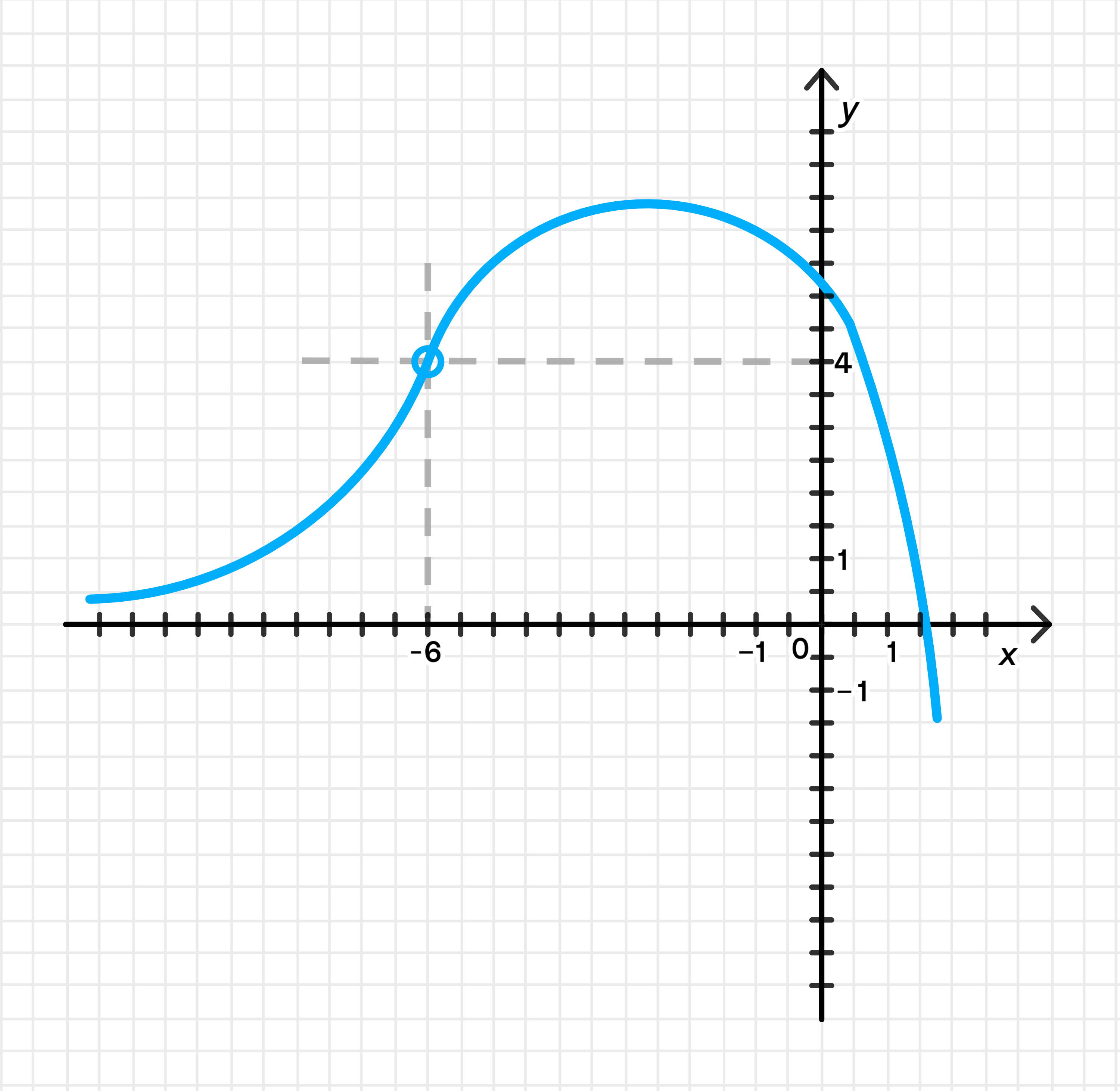
б) и
Условие: График функции должен показывать, что при функция стремится к 4, а при функция стремится к 0.
1. Пояснение:
- В точке , функция имеет предел 4, что означает, что при подходе к этой точке с обеих сторон (слева и справа) значение функции стремится к 4.
- Когда , функция стремится к горизонтальной асимптоте , что означает, что график функции приближается к оси при стремящемся к минус бесконечности.
2. Как построить график:
- Нарисуйте вертикальную асимптоту или плавный подход функции в точке , стремящуюся к .
- Для функция должна стремиться к горизонтальной линии на уровне .
- Убедитесь, что график не пересекает ось для больших отрицательных значений , а только стремится к этой линии.
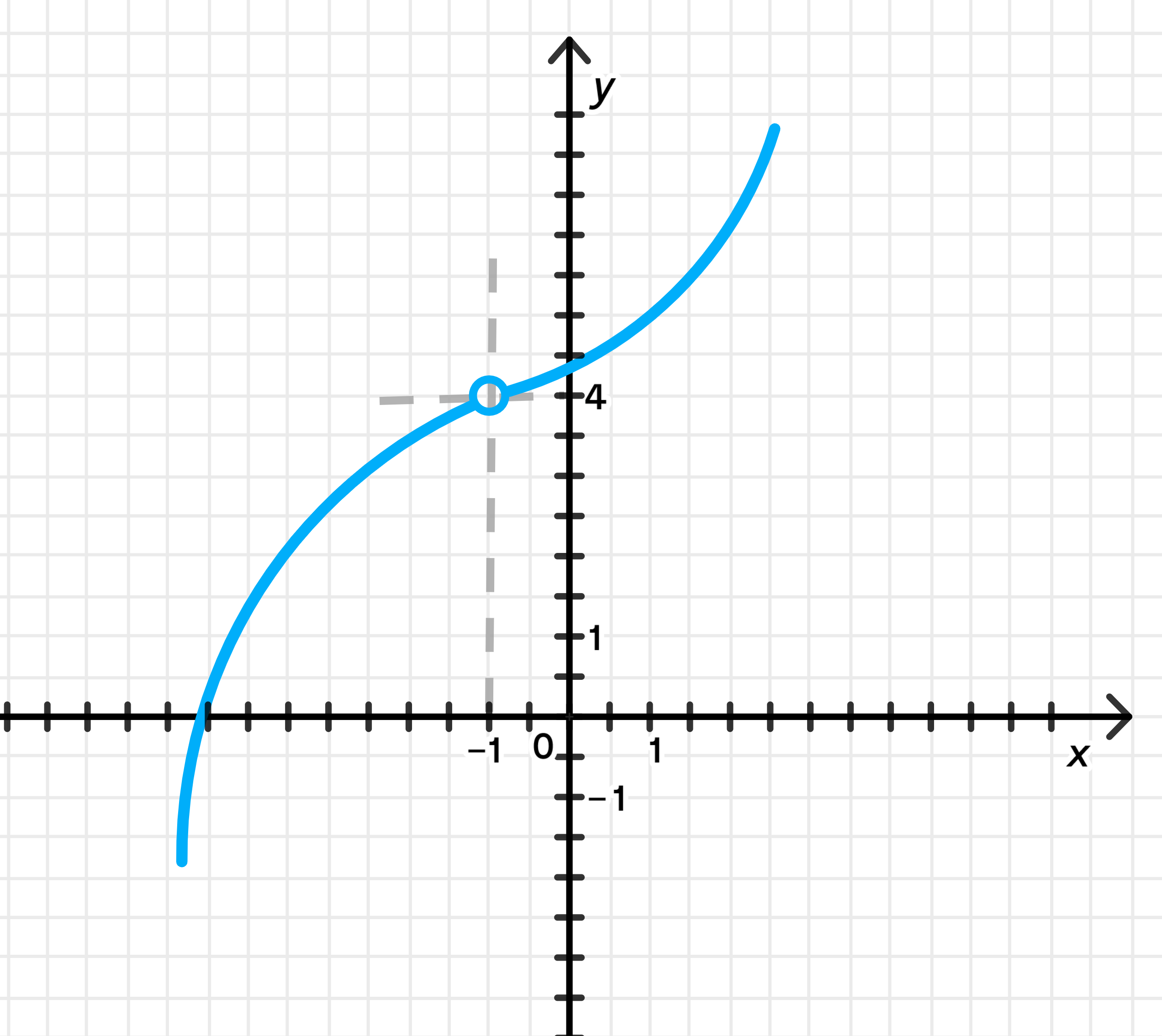
в) и не существует
Условие: График функции должен показывать, что при функция стремится к 4, но в самой точке функция не существует.
1. Пояснение:
- Предел функции при равен 4, что означает, что с обеих сторон от точки функция стремится к значению 4.
- Однако в самой точке функция не существует, что указывает на разрыв. Это может быть как бесконечным разрывом (функция стремится к бесконечности), так и скачком, где значение функции с одной стороны отличается от значения с другой стороны.
2. Как построить график:
- Нарисуйте вертикальную асимптоту или разрыв в точке .
- С обеих сторон от точки функция будет стремиться к , но не будет пересекать эту точку.
- Это будет выглядеть как две разные части кривой, которые стремятся к одной и той же горизонтальной линии, но не достигают её в точке .
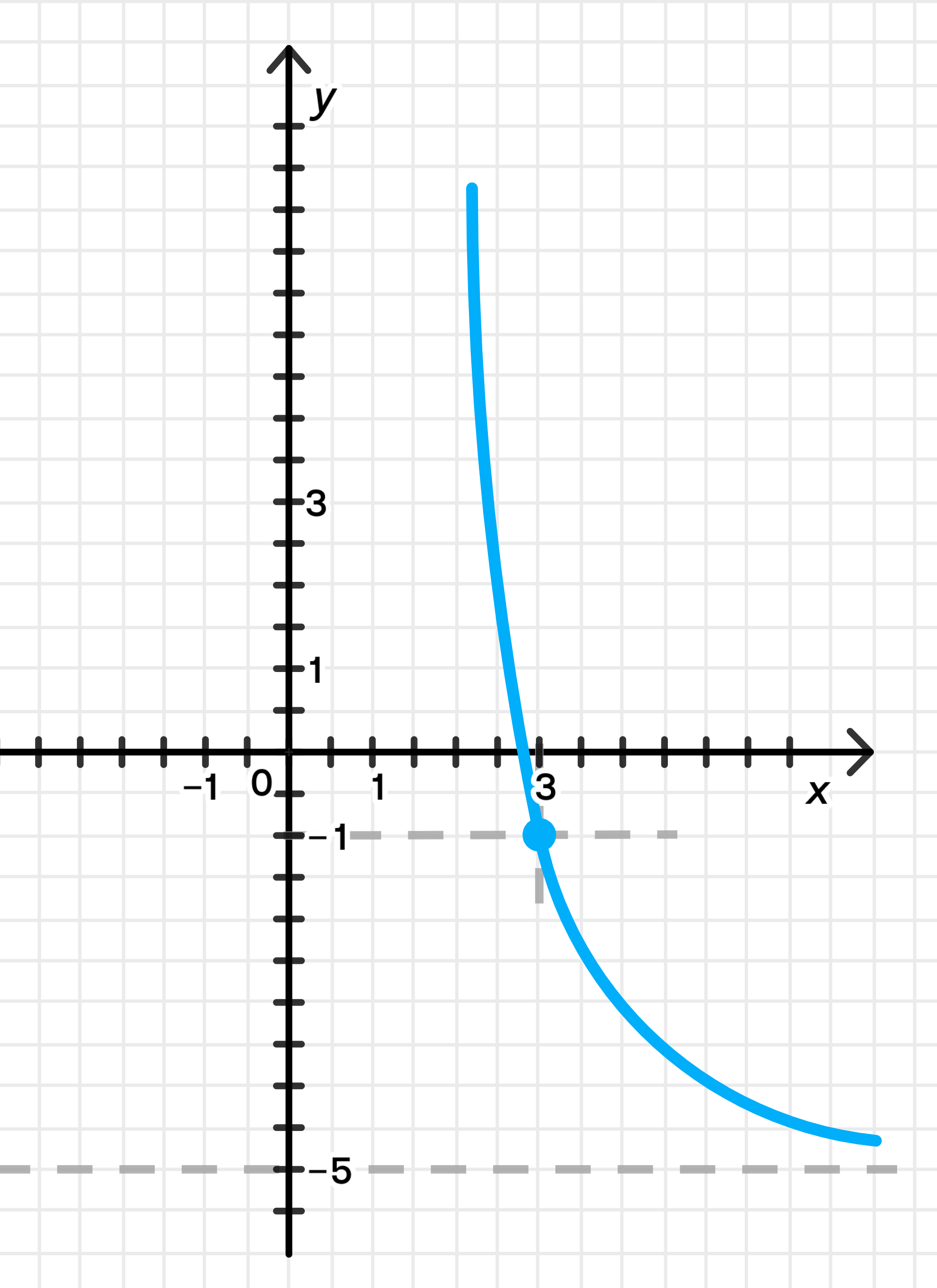
г) и
Условие: График функции должен показывать, что при функция стремится к -1, а при функция стремится к -5.
1. Пояснение:
- В точке , предел функции равен -1, что означает, что при подходе к этой точке с обеих сторон функция стремится к значению .
- При , функция стремится к горизонтальной асимптоте на уровне , что означает, что график будет приближаться к оси при увеличении значения .
2. Как построить график:
- В точке нарисуйте точку на графике.
- Построьте график, который стремится к точке с обеих сторон, без разрывов или скачков.
- Для больших значений график должен стремиться к горизонтальной асимптоте , не пересекающей её.