Алгебра Профильный Уровень
10 класс задачник профильный уровень Мордкович
10 класс
Тип
ГДЗ, Решебник.
Автор
А.Г. Мордкович, П. В. Семенов.
Год
2015-2020.
Издательство
Мнемозина.
Описание
Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 39.22 Профильный Уровень Мордкович — Подробные Ответы
Задача
Построьте график функции , обладающей следующими свойствами:
а) ; ; ; ; ;
функция возрастает на ;
б) ; ; ; ; ;
.
Подробный ответ:
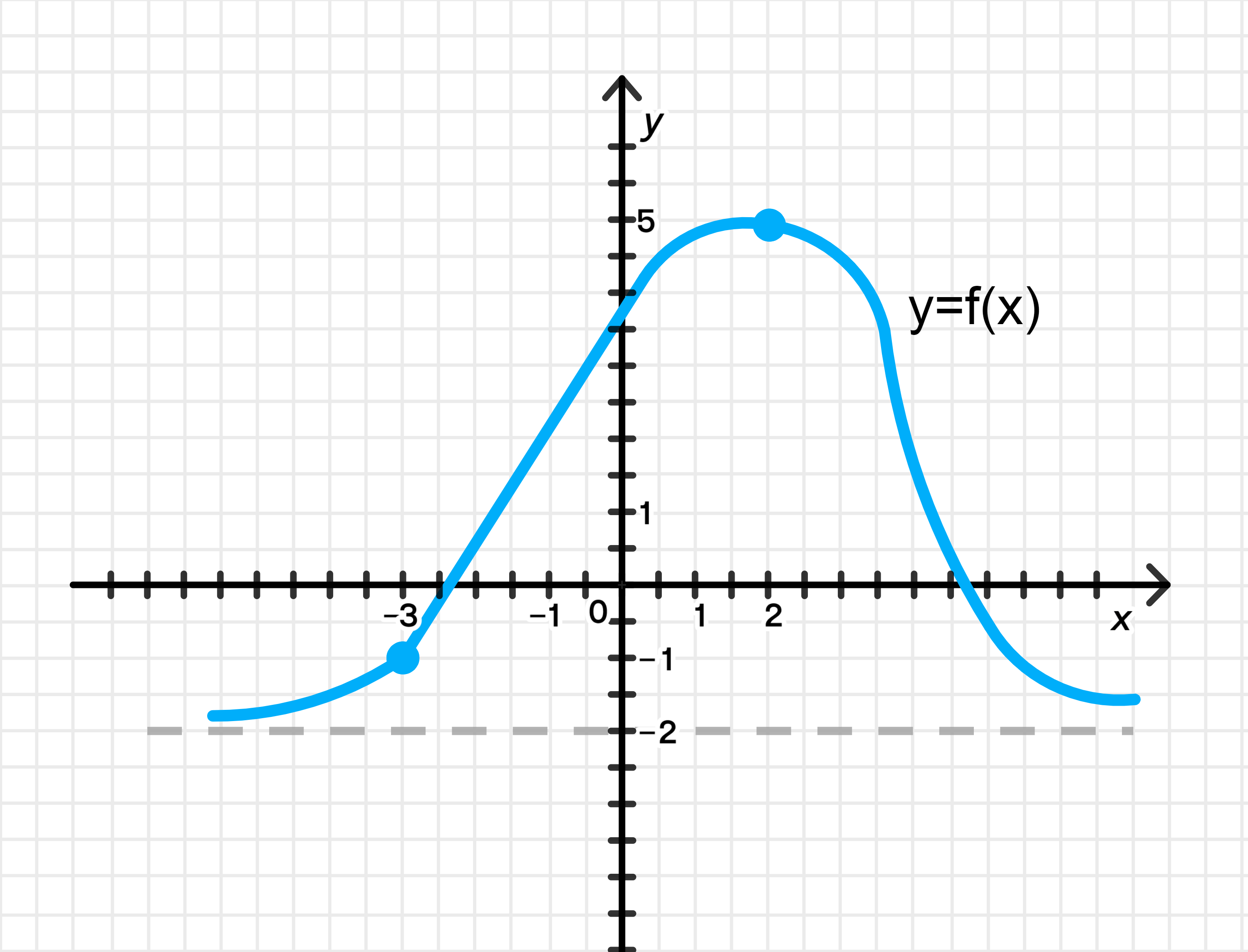
а) Свойства функции:
:
- Это означает, что функция стремится к значению 5, когда приближается к 2, и сама функция в точке также равна 5.
- Визуально на графике это означает, что точка лежит на графике функции, и функция не имеет разрыва или скачка в этой точке. График будет плавно проходить через эту точку.
:
- В точке функция имеет разрыв. Когда стремится к , значение функции стремится к , но сама функция в точке имеет значение 1.
- На графике мы увидим разрыв: линия будет приближаться к с обеих сторон, но в самой точке будет «прыжок» вверх до значения 1. Таким образом, точка будет являться дискретной точкой (на графике будет изображена как отдельная точка), а линия будет обходить её с обеих сторон, приближаясь к .
:
- Это означает, что функция имеет горизонтальную асимптоту на уровне при .
- На графике линия будет стремиться к значению при увеличении , но никогда не пересечет эту ось. Это можно изобразить как линию, которая будет очень близка к , но не достигнет её.
Возрастает на :
- Функция возрастает на интервале , что означает, что при в этом интервале значение функции будет увеличиваться.
- На графике это выглядит как линия, которая поднимается (растет) слева от точки . В точке функция может иметь максимальное значение на этом интервале, если это локальный максимум.
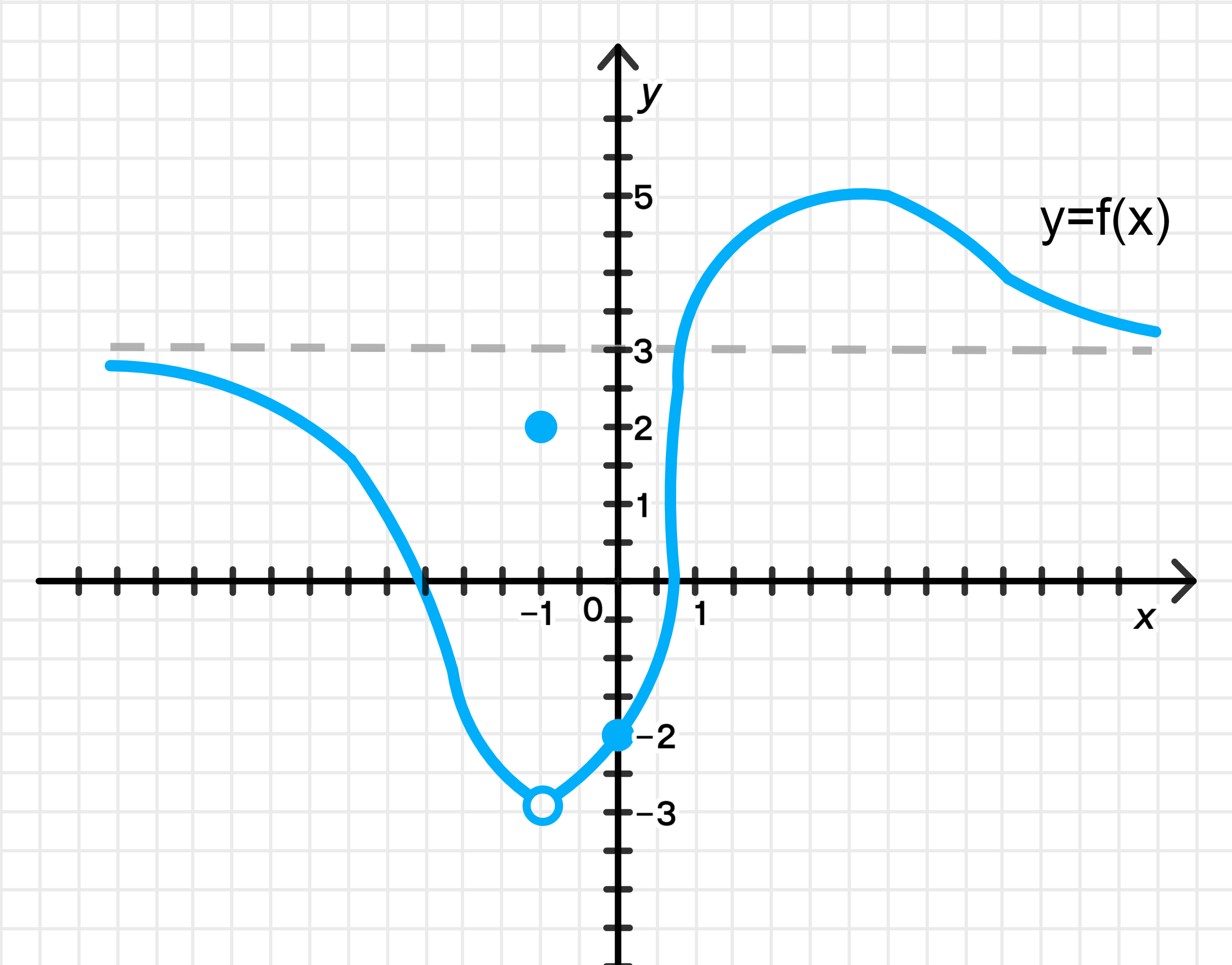
б) Свойства функции:
:
- Это означает, что функция стремится к значению , когда , но сама функция в точке равна 2.
- График будет иметь разрыв: с обеих сторон от функция будет приближаться к , но в самой точке график перескочит вверх до значения 2. Это выглядит как «прыжок» на графике.
:
- В точке функция имеет значение , и в окрестности этой точки функция стремится к .
- График будет гладким и непрерывным в точке . Точка будет лежать на графике, и линия будет плавно проходить через неё.
:
- Это означает, что функция имеет горизонтальную асимптоту на уровне при .
- На графике линия будет стремиться к значению при увеличении , но не пересечет эту ось. Функция будет «приближаться» к этой линии, но никогда не пересечет её.
:
- Это означает, что множество значений функции лежит в интервале от до 5, включая 5, но не включая .
- Это ограничивает график функции сверху (значения не могут превышать 5) и снизу (значения функции не могут быть меньше ).
Построение графика:
Отметьте точки и асимптоты:
- Начнем с того, что необходимо отметить ключевые точки:
- — функция достигает значения 5.
- — разрыв, функция приближается к , но в точке имеет значение 1.
- — разрыв, функция приближается к , но в точке имеет значение 2.
- — точка, где функция равна .
- Также нанесем асимптоты:
- Горизонтальная асимптота при (для части графика, которая идет вправо).
- Горизонтальная асимптота при (для части графика, которая идет влево).
Рисуем участки графика:
- Для интервала функция возрастает, и мы рисуем линию, которая поднимается до точки .
- Для функция будет стремиться к значению , но будет иметь разрыв в точке , где функция перескакивает до 1.
- После точки мы видим ещё один разрыв, и функция будет стремиться к значению .
- В окрестности , линия будет плавно проходить через точку .
- Для функция будет приближаться к асимптотам и , соответственно.
Таким образом, график будет состоять из нескольких частей, каждая из которых будет строго следовать за описанными свойствами.
Комментарии
Другие предметы