ГДЗ по Алгебре 10 Класс Номер 39.5 Профильный Уровень Мордкович — Подробные Ответы

Постройте график какой-либо функции у = f(x), обладающей указанными свойствами:

а) $\lim_{x \to \infty} f(x) = 3$

б) $\lim_{x \to \infty} f(x) = -2$

в) $\lim_{x \to \infty} f(x) = 5$

г) $\lim_{x \to \infty} f(x) = 0$

а) $\lim_{x \to \infty} f(x) = 3$:

б) $\lim_{x \to \infty} f(x) = -2$:

в) $\lim_{x \to \infty} f(x) = 5$:

г) $\lim_{x \to \infty} f(x) = 0$:

Нам необходимо построить график функции $y = f(x)$, которая будет обладать свойствами, связанными с пределами на бесконечности. Конкретно, функция должна иметь пределы:

• $\lim_{x \to \infty} f(x) = 3$,
• $\lim_{x \to \infty} f(x) = -2$,
• $\lim_{x \to \infty} f(x) = 5$,
• $\lim_{x \to \infty} f(x) = 0$.

Задача состоит в том, чтобы создать график функции, который будет соответствовать этим предельным значениям при $x \to \infty$.

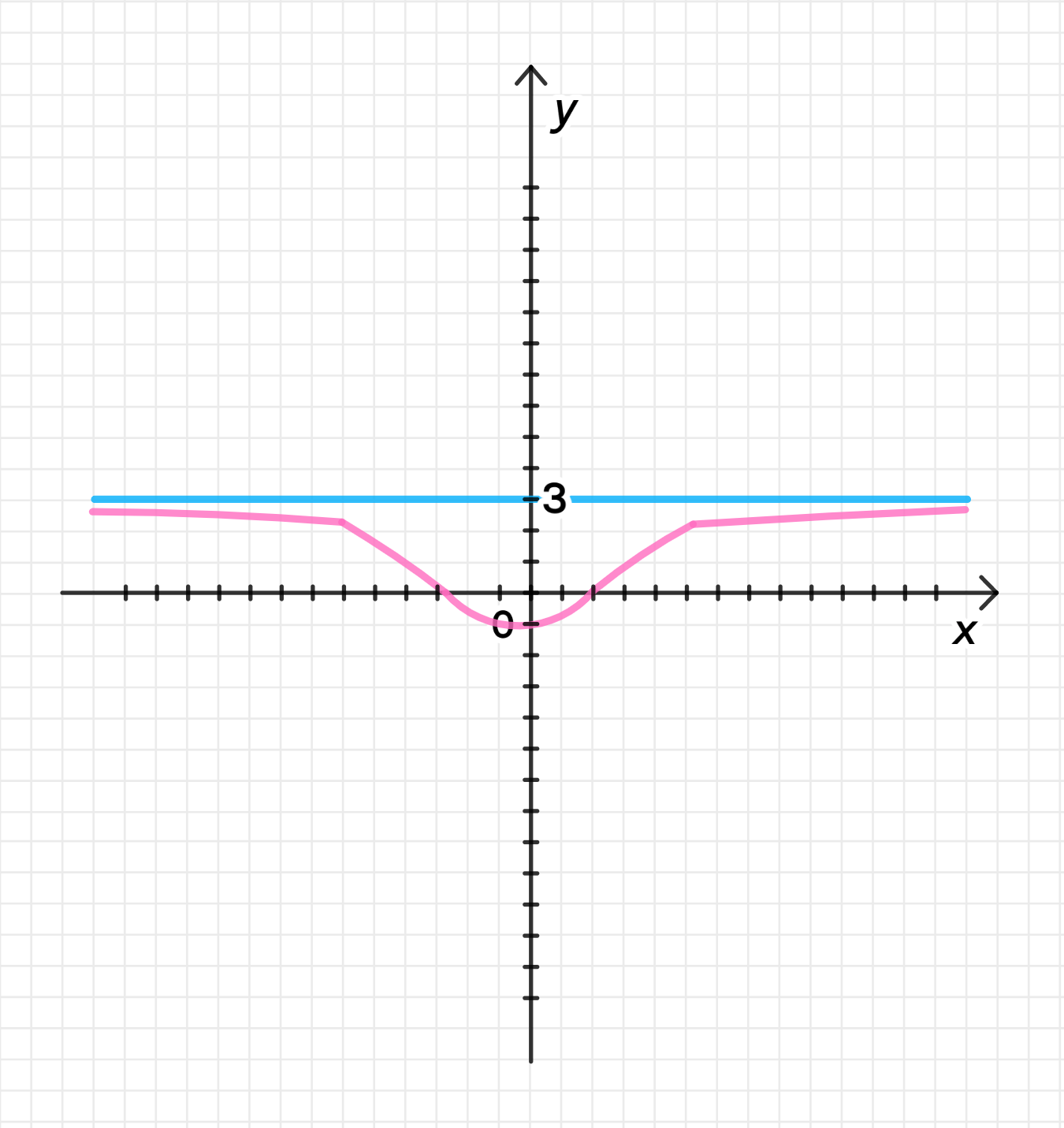
а) Функция с пределом $\lim_{x \to \infty} f(x) = 3$

Интуиция и шаги построения:

Описание функции: Функция должна стремиться к значению 3 при $x \to \infty$. Это означает, что с увеличением $x$, функция будет все ближе и ближе к 3, но не будет её пересекать. Это может быть обычная асимптота на уровне $y = 3$.

Пример функции:
Одним из примеров может быть функция вида:

$$f(x) = 3 — \frac{1}{x}$$

Такая функция на больших $x$ будет приближаться к 3, так как с увеличением $x$ выражение $\frac{1}{x}$ становится все меньше и меньше, и функция стабилизируется на уровне 3.

Строительство графика:

• На графике мы видим горизонтальную асимптоту, проходящую через $y = 3$.
• Функция будет идти снизу вверх, приближаясь к линии $y = 3$, но не пересекает её.

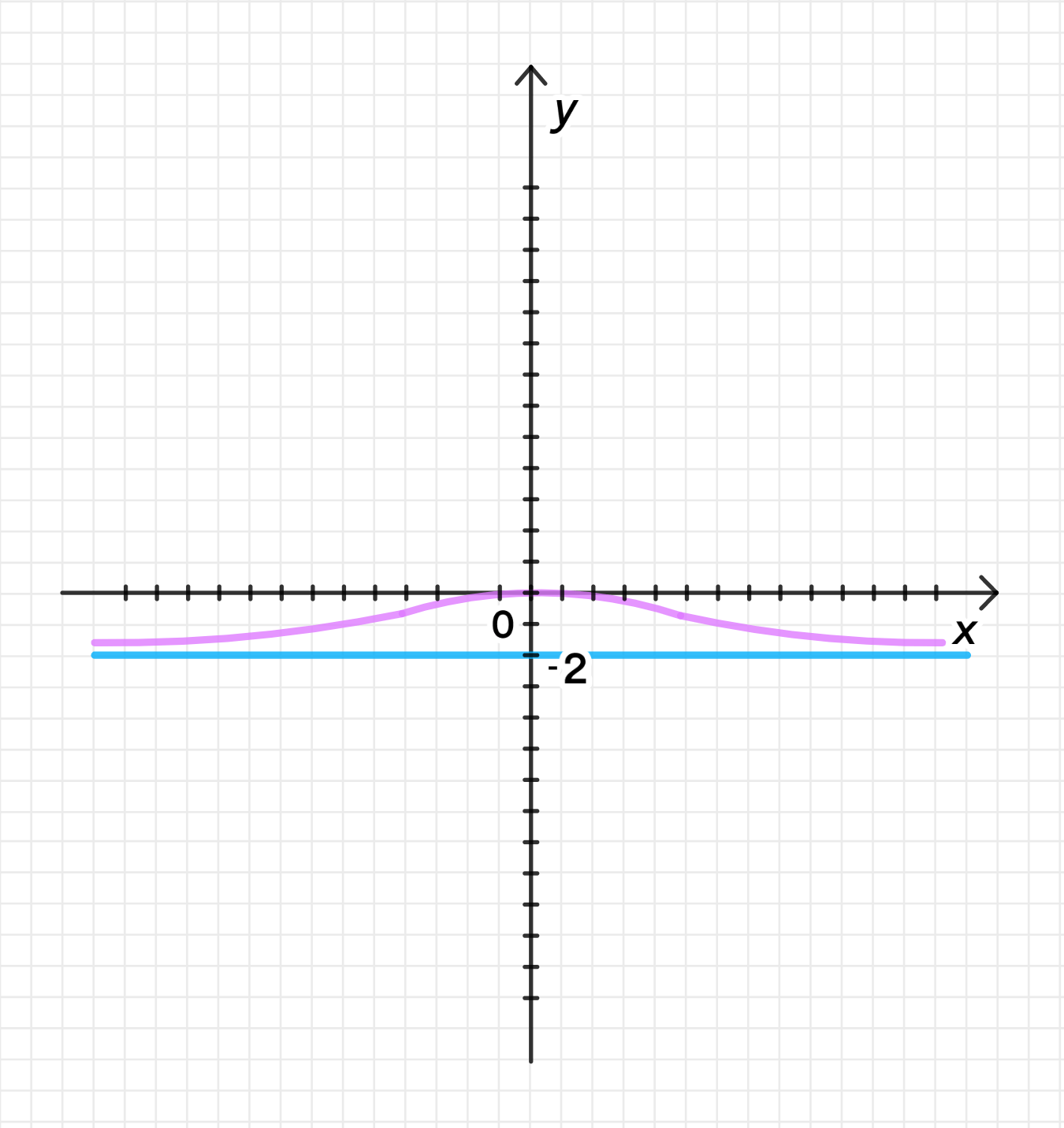
б) Функция с пределом $\lim_{x \to \infty} f(x) = -2$

Интуиция и шаги построения:

Описание функции: Эта функция будет стремиться к значению $-2$ на бесконечности. Подобно предыдущему случаю, функция будет иметь горизонтальную асимптоту, которая проходит через $y = -2$.

Пример функции:
Одним из примеров может быть функция вида:

$$f(x) = -2 + \frac{1}{x}$$

Эта функция при $x \to \infty$ будет стремиться к $-2$, так как $\frac{1}{x}$ будет уменьшаться с увеличением $x$, и функция стабилизируется на уровне $-2$.

Строительство графика:

• На графике будет горизонтальная линия на уровне $y = -2$.
• Функция будет стремиться к этой линии, не пересекает её.

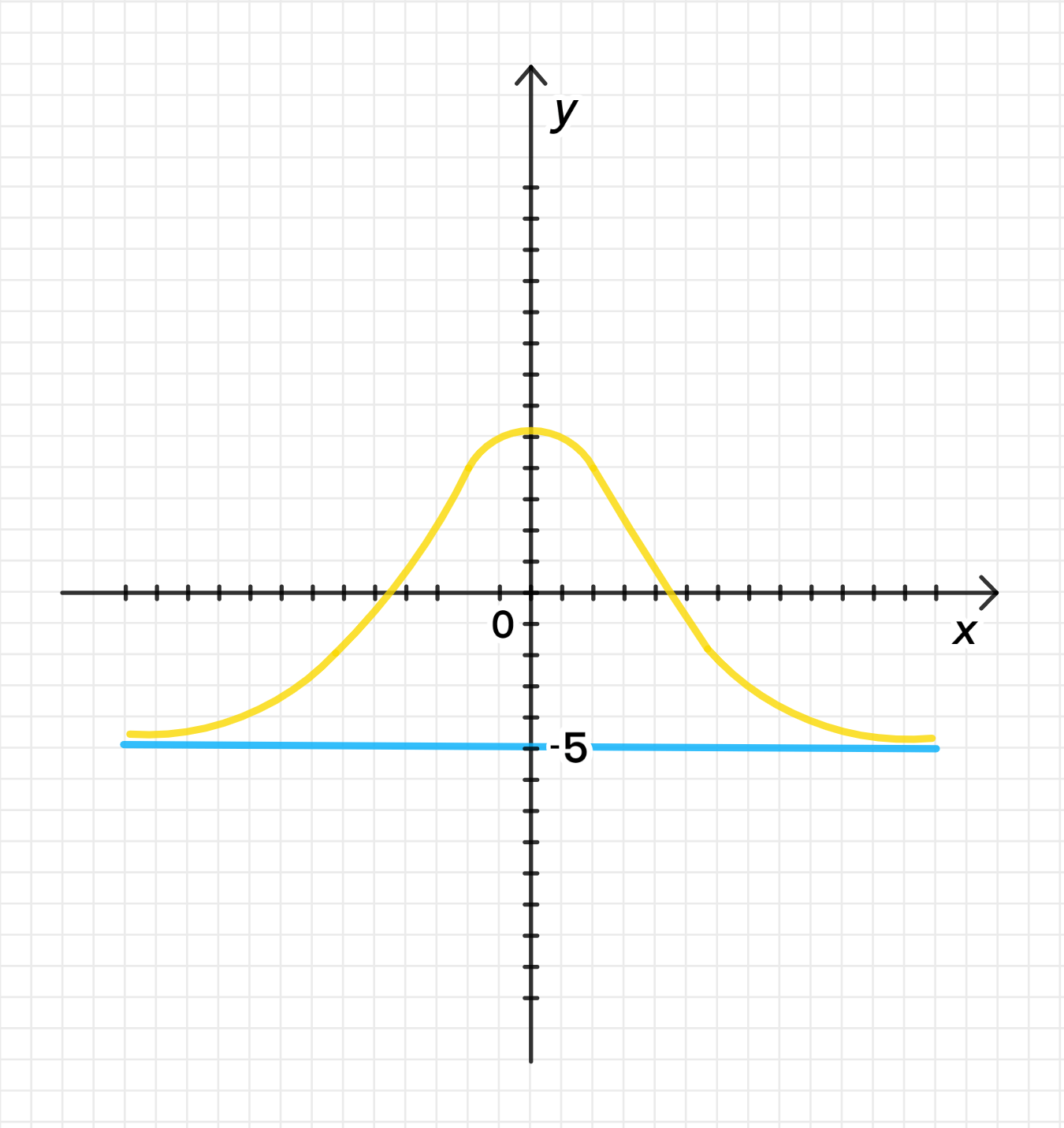
в) Функция с пределом $\lim_{x \to \infty} f(x) = 5$

Интуиция и шаги построения:

Описание функции: В данном случае функция должна стремиться к значению 5 при $x \to \infty$. Аналогично предыдущим примерам, на графике будет горизонтальная асимптота на уровне $y = 5$.

Пример функции:
Одна из возможных функций:

$$f(x) = 5 — \frac{2}{x}$$

Здесь $\frac{2}{x}$ будет стремиться к нулю при увеличении $x$, а функция будет стремиться к значению 5.

Строительство графика:

• На графике будет горизонтальная линия на уровне $y = 5$.
• Функция будет стремиться к этой линии, но не будет её пересекать.

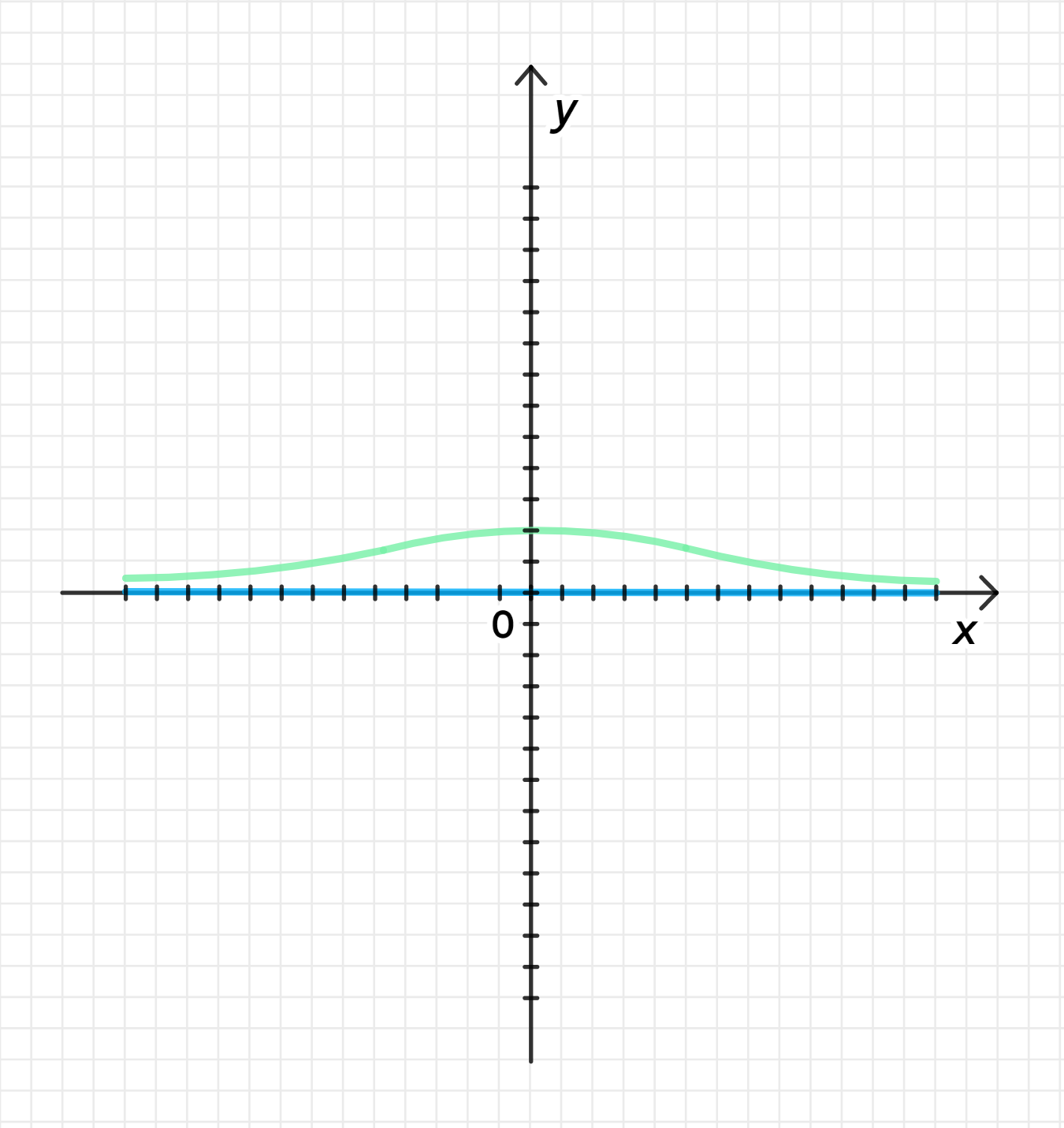
г) Функция с пределом $\lim_{x \to \infty} f(x) = 0$

Интуиция и шаги построения:

Описание функции: Здесь функция должна стремиться к нулю при $x \to \infty$. Это будет означать, что функция будет «прижиматься» к оси $x$ и не будет пересекать её.

Пример функции:
Примером такой функции может быть:

$$f(x) = \frac{1}{x}$$

При $x \to \infty$, эта функция будет стремиться к нулю.

Строительство графика:

• График будет стремиться к оси $x$ (где $y = 0$), но не будет её пересекать.
• Функция будет очень близка к оси $x$ для больших значений $x$.