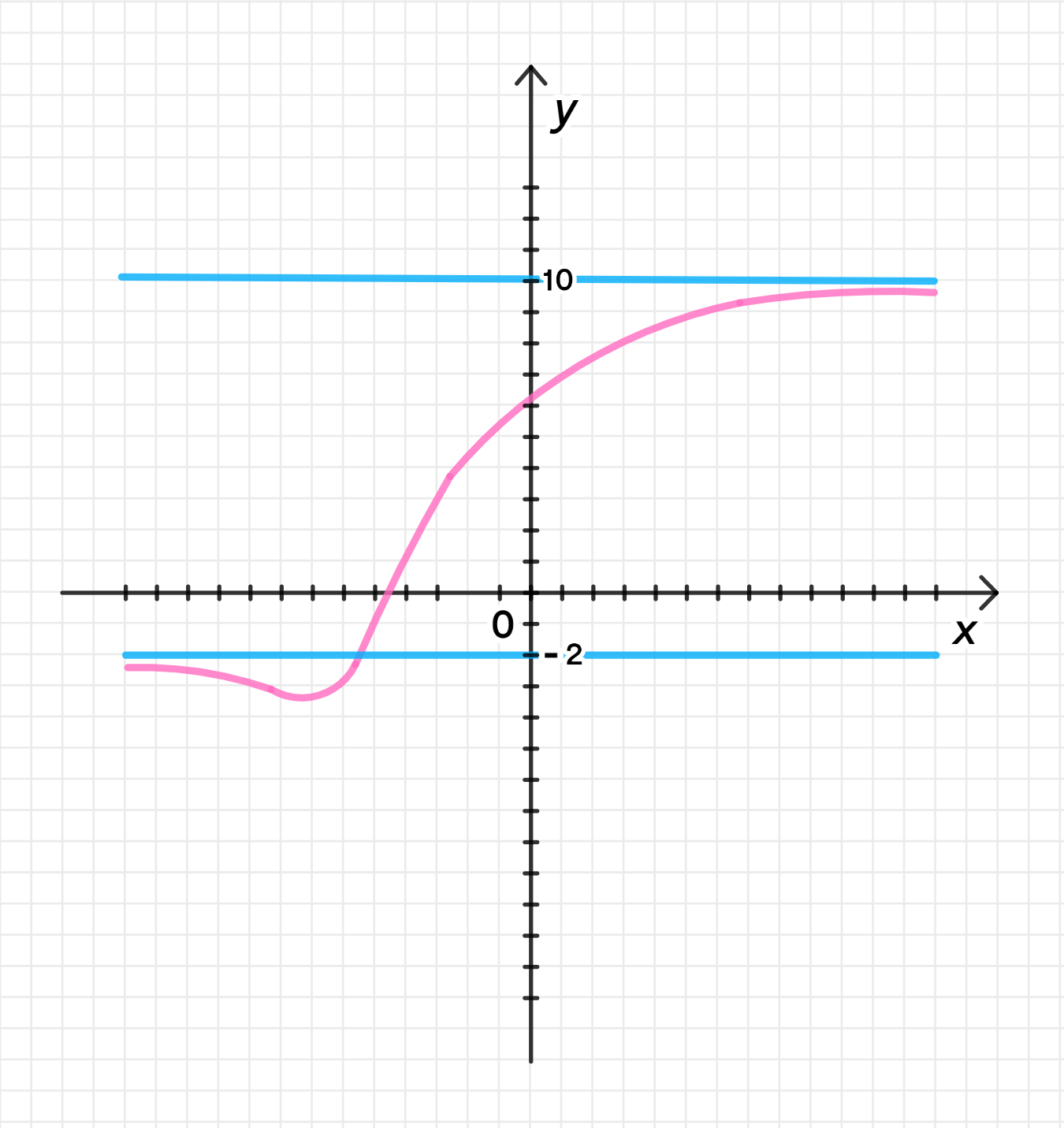ГДЗ по Алгебре 10 Класс Номер 39.6 Профильный Уровень Мордкович — Подробные Ответы

Постройте график какой-либо функции у = f(x), обладающей указанными свойствами:

а) $\lim_{x \to \infty} f(x) = 4$ и $\lim_{x \to -\infty} f(x) = 0$

б) $\lim_{x \to \infty} f(x) = 10$ и $\lim_{x \to -\infty} f(x) = -2$

в) $\lim_{x \to \infty} f(x) = -2$ и $\lim_{x \to -\infty} f(x) = 1$

г) $\lim_{x \to \infty} f(x) = 3$ и $\lim_{x \to -\infty} f(x) = -4$

а) $\lim_{x \to \infty} f(x) = 4$ и $\lim_{x \to -\infty} f(x) = 0$:

б) $\lim_{x \to \infty} f(x) = 10$ и $\lim_{x \to -\infty} f(x) = -2$:

в) $\lim_{x \to \infty} f(x) = -2$ и $\lim_{x \to -\infty} f(x) = 1$:

г) $\lim_{x \to \infty} f(x) = 3$ и $\lim_{x \to -\infty} f(x) = -4$:

1. Выбор функции

Для каждой из функций выбраны простые рациональные выражения, у которых есть горизонтальные асимптоты. Мы рассмотрим четыре функции, каждая из которых имеет особое поведение на больших значениях $x$:

• а) $f(x) = \frac{4x}{x+1}$
• б) $f(x) = \frac{12x}{x+1}$
• в) $f(x) = \frac{-2x}{x+1}$
• г) $f(x) = \frac{7x}{x+2}$

2. Принципы построения графиков

Графики для этих функций строятся с учетом того, что на больших значениях $x$ функции стремятся к определенным горизонтальным асимптотам.

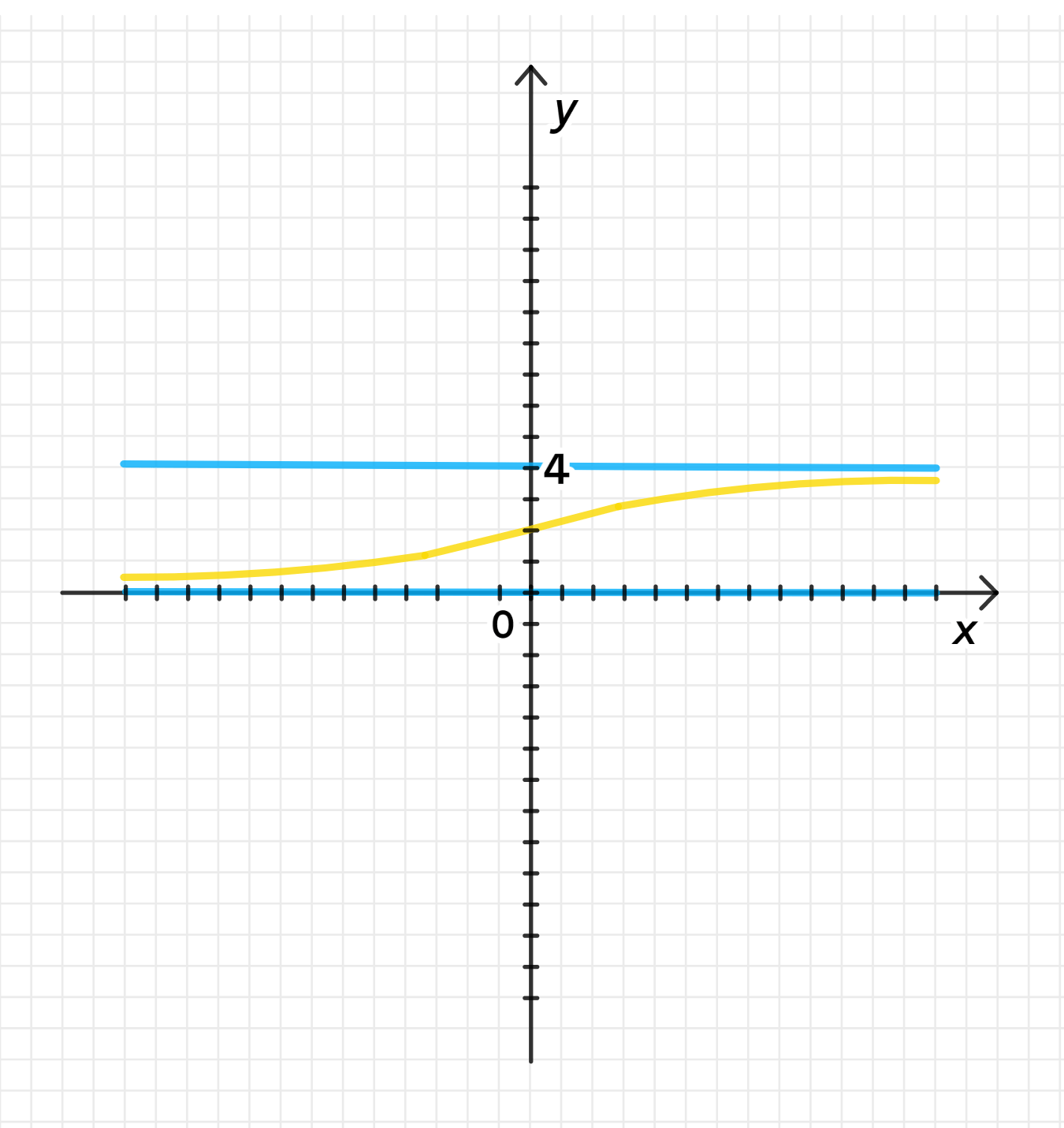
Для функции а):

• При $x \to \infty$, функция стремится к 4.
• При $x \to -\infty$, функция стремится к 0.
• Это означает, что график будет приближаться к прямой $y = 4$ при увеличении $x$ и будет стремиться к оси $y = 0$ при уменьшении $x$.

Для функции б):

• При $x \to \infty$, функция стремится к 10.
• При $x \to -\infty$, функция стремится к -2.
• График будет стремиться к прямой $y = 10$ для больших $x$ и к прямой $y = -2$ для малых $x$.

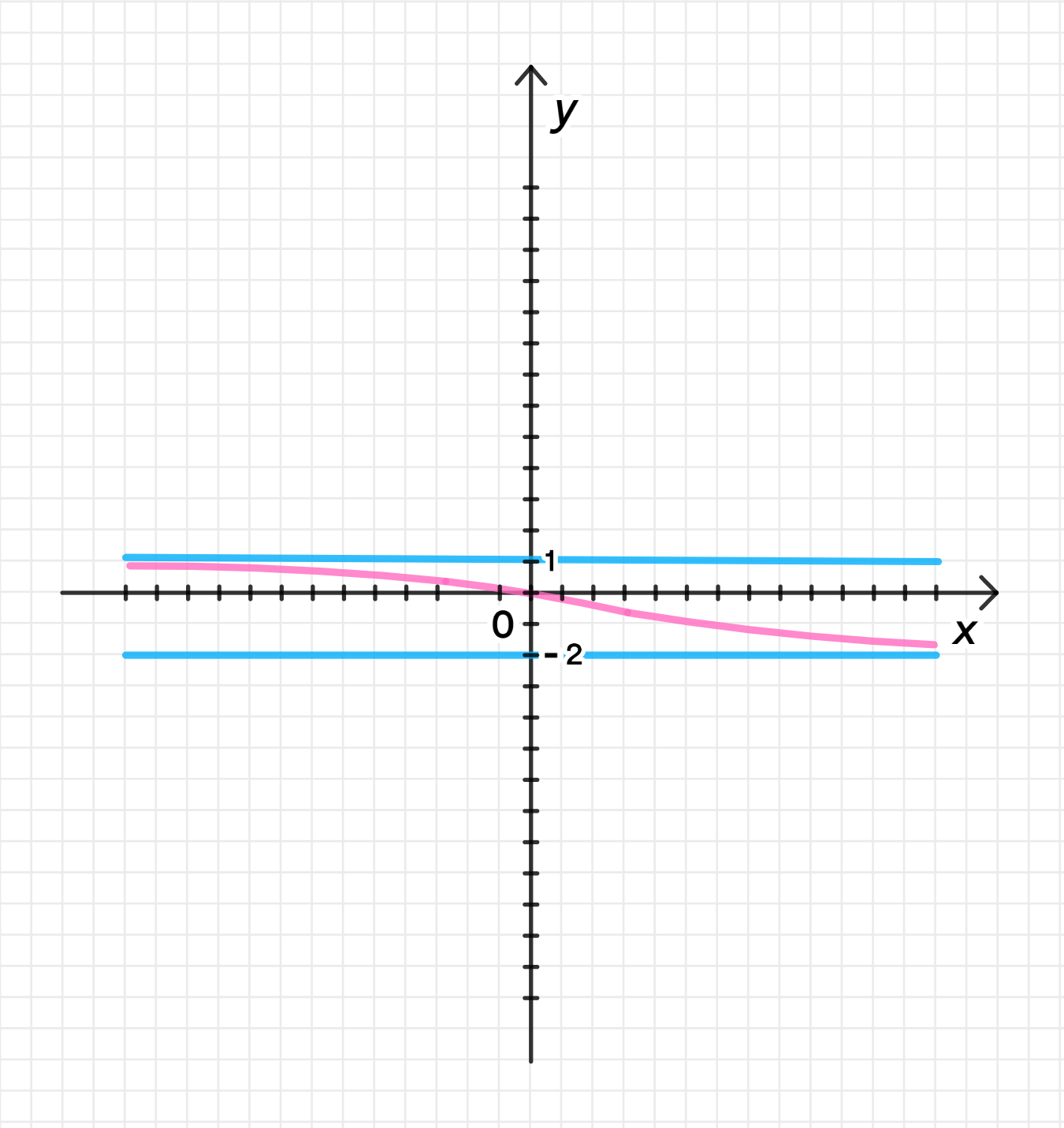
Для функции в):

• При $x \to \infty$, функция стремится к -2.
• При $x \to -\infty$, функция стремится к 1.
• График будет стремиться к прямой $y = -2$ для больших $x$ и к прямой $y = 1$ для малых $x$.

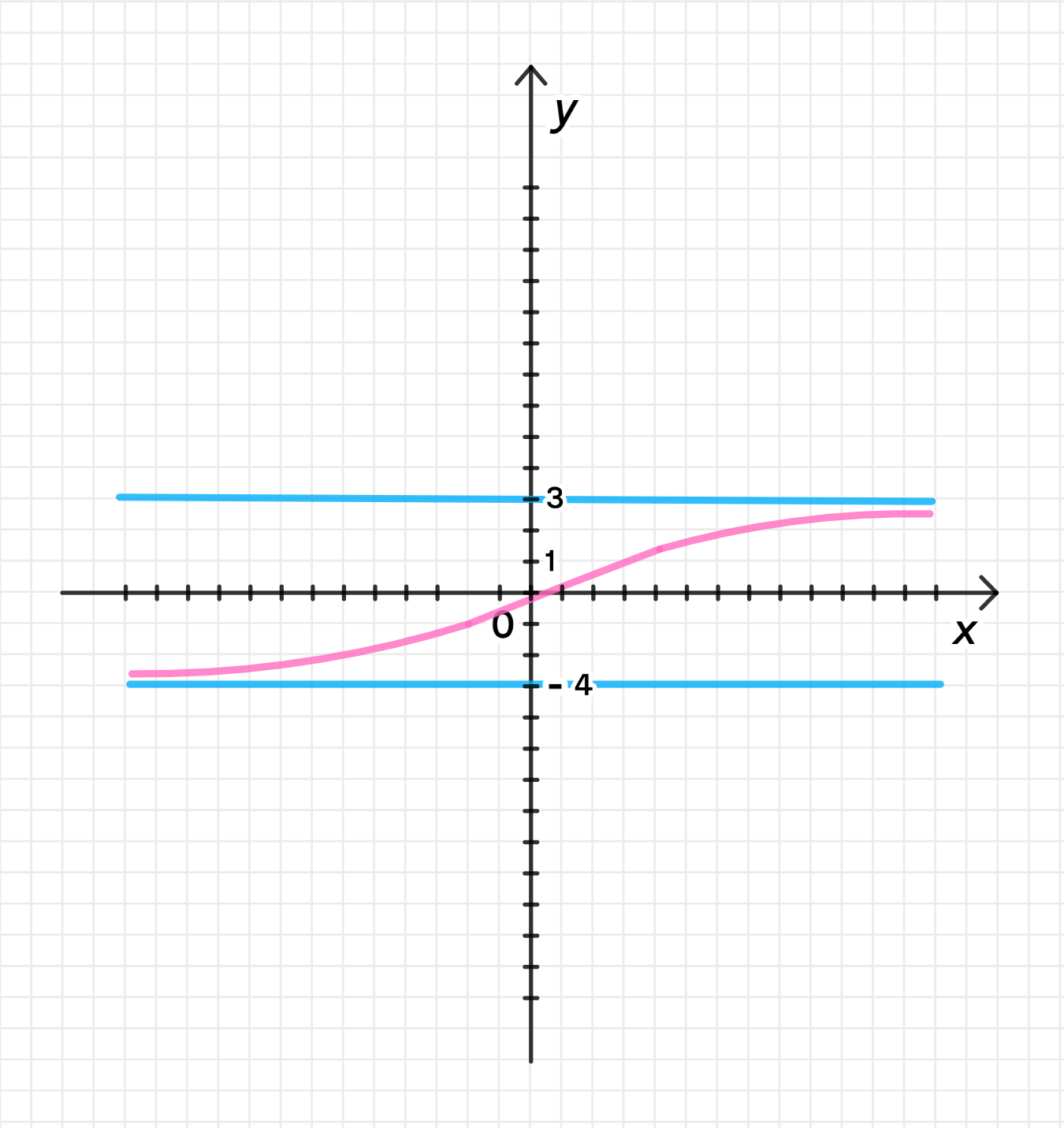
Для функции г):

• При $x \to \infty$, функция стремится к 3.
• При $x \to -\infty$, функция стремится к -4.
• График будет стремиться к прямой $y = 3$ для больших $x$ и к прямой $y = -4$ для малых $x$.

3. Построение графиков

Чтобы построить график этих функций:

1. Выбор диапазона $x$:
   Для каждого графика важно выбрать диапазон $x$, который охватывает как положительные, так и отрицательные значения $x$. Например, можно выбрать диапазон от -20 до 20.
2. Вычисление значений функции:
   Для каждого значения $x$ в выбранном диапазоне нужно вычислить значение функции $f(x)$. Это можно сделать с помощью простых вычислений вручную или с использованием инструментов, таких как Python.
3. Построение графика:
   Используя программное обеспечение или язык программирования (например, Python с библиотеками Matplotlib или NumPy), можно построить график функции. На графике следует отметить горизонтальные линии, которые показывают асимптоты:

а) горизонтальная линия $y = 4$ и $y = 0$.

б) горизонтальная линия $y = 10$ и $y = -2$.

в) горизонтальная линия $y = -2$ и $y = 1$.

г) горизонтальная линия $y = 3$ и $y = -4$.

4. Итоговые наблюдения

• Графики этих функций будут иметь горизонтальные асимптоты, которые мы заранее определили для каждого случая.
• На графиках будет видно, как функция приближается к своей горизонтальной асимптоте при больших значениях $x$ и как она ведет себя при малых значениях $x$.