ГДЗ по Алгебре 10 Класс Номер 39.7 Профильный Уровень Мордкович — Подробные Ответы

Постройте график какой-либо функции у = f(x), обладающей указанными свойствами:

а) $\lim_{x \to \infty} f(x) = 5$ и $f(x) > 0$ на $(-∞; +∞)$

б) $\lim_{x \to -\infty} f(x) = -3$ и $f(x) \geq 0$ на отрезке $[-7; 3]$

в) $\lim_{x \to \infty} f(x) = 0$ и $f(x) > 0$ на $[0; +∞)$

г) $\lim_{x \to -\infty} f(x) = 0$ и $f(x) < 0$ на $(-∞; +∞)$

а) $\lim_{x \to \infty} f(x) = 5$ и $f(x) > 0$ на $(-∞; +∞)$:

б) $\lim_{x \to -\infty} f(x) = -3$ и $f(x) \geq 0$ на отрезке $[-7; 3]$:

в) $\lim_{x \to \infty} f(x) = 0$ и $f(x) > 0$ на $[0; +∞)$:

г) $\lim_{x \to -\infty} f(x) = 0$ и $f(x) < 0$ на $(-∞; +∞)$:

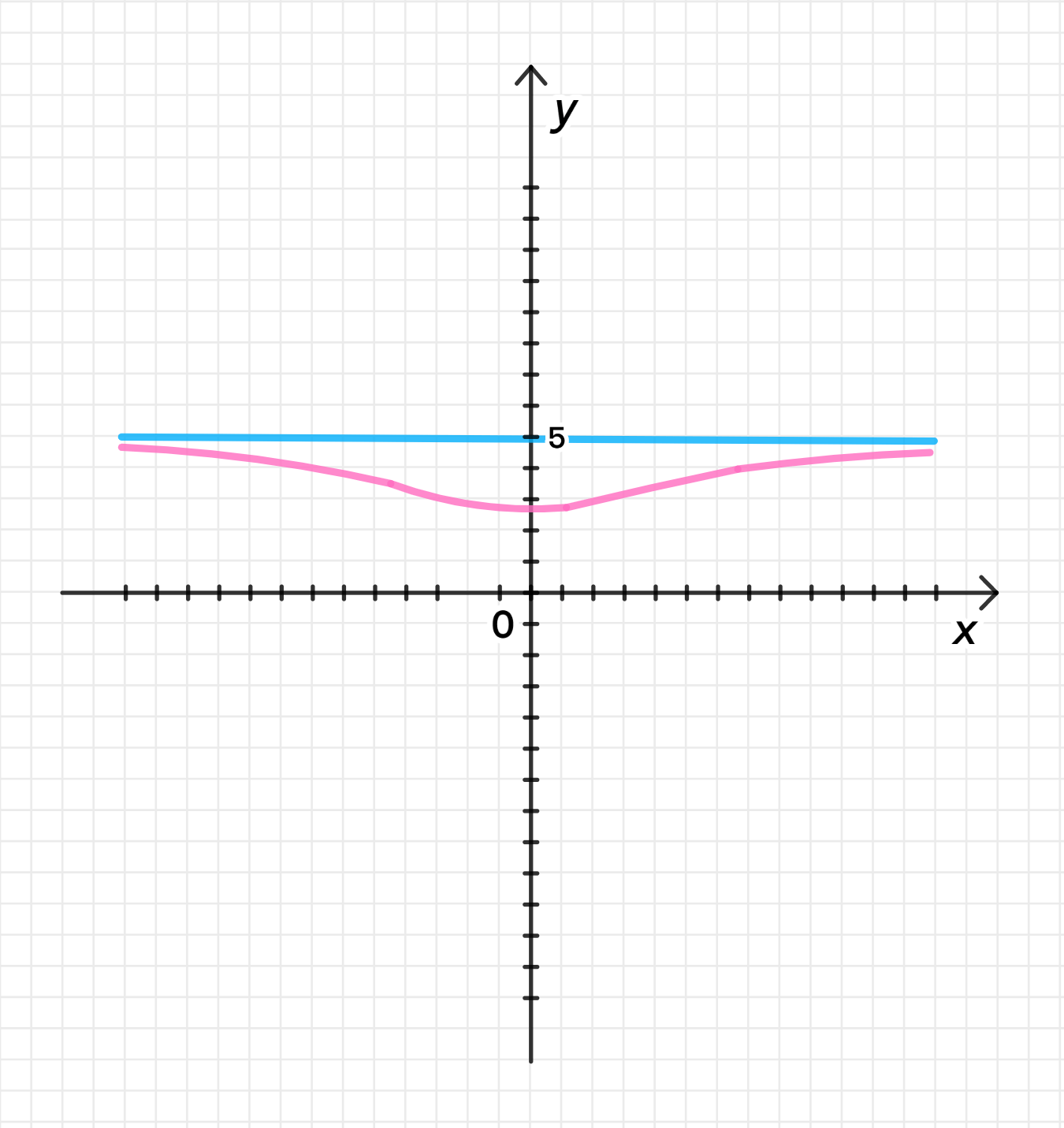
а)

Функция: $\lim_{x \to \infty} f(x) = 5$ и $f(x) > 0$ на $(-∞; +∞)$.

Для этого условия можно выбрать функцию:

$$f(x) = 5 + \frac{1}{x^2 + 1}$$

Шаги построения:

• Функция $f(x)$ всегда больше нуля, так как знаменатель $x^2 + 1$ всегда положителен.
• При $x \to \infty$, дробь $\frac{1}{x^2 + 1}$ стремится к 0, следовательно, $f(x)$ стремится к 5.
• При $x \to -\infty$, аналогично, $f(x)$ также стремится к 5, так как $\frac{1}{x^2 + 1}$ снова становится очень маленьким.
• График будет асимптотично приближаться к 5 с обеих сторон.

Как построить:

1. Для разных значений $x$ вычисляйте $f(x)$.
2. Отметьте значения $f(x)$, чтобы увидеть, как график стремится к 5, когда $x$ увеличивается или уменьшается.
3. График будет иметь форму, похожую на гиперболу, которая никогда не пересечет горизонтальную прямую $y = 5$.

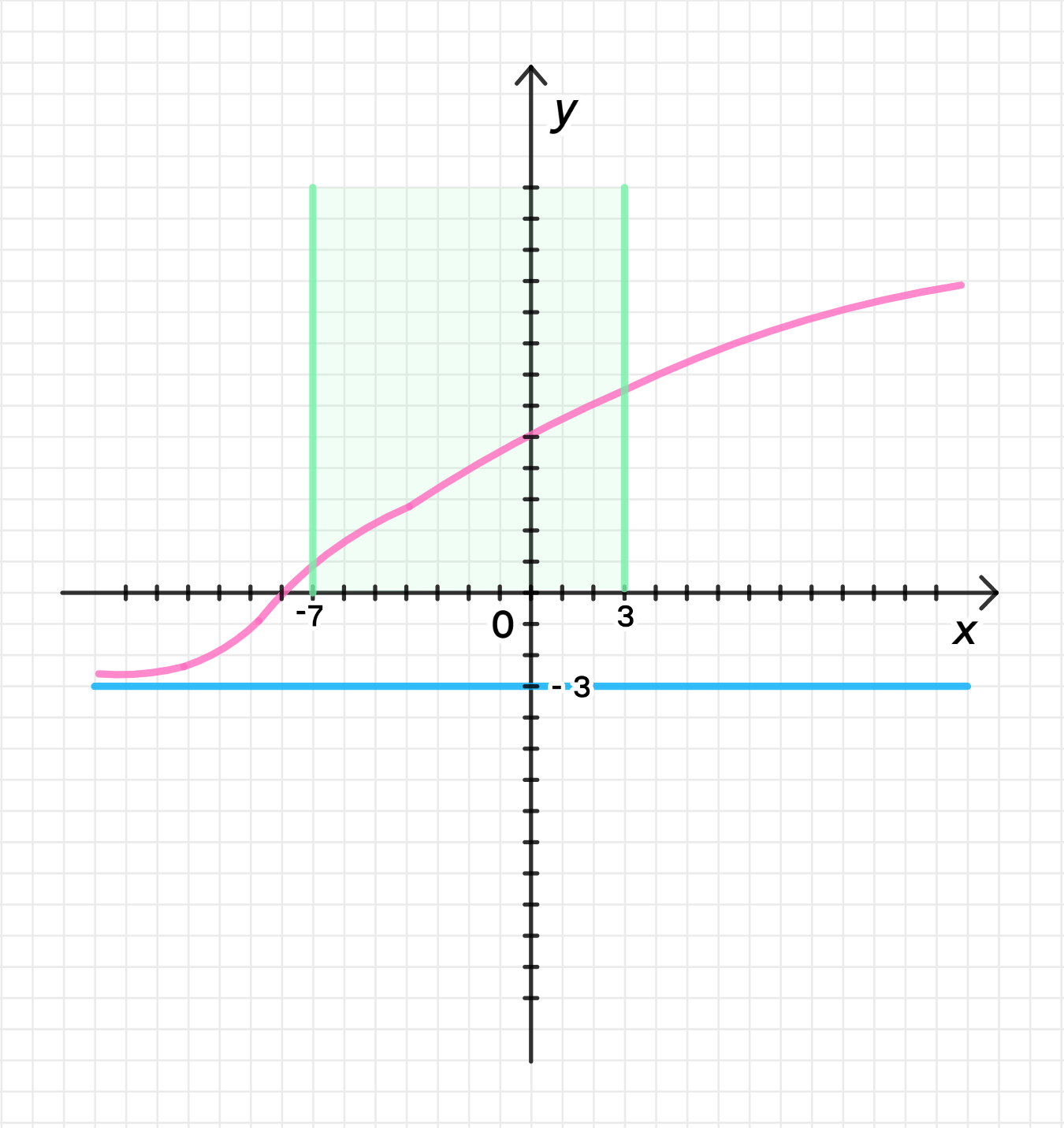
б)

Функция: $\lim_{x \to -\infty} f(x) = -3$ и $f(x) \geq 0$ на отрезке $[-7; 3]$.

Предлагаемая функция:

$$f(x) = -3 + \frac{6}{(x + 5)^2 + 1}$$

Шаги построения:

• При $x \to -\infty$, выражение $\frac{6}{(x + 5)^2 + 1}$ стремится к 0, и функция $f(x)$ стремится к $-3$.
• На отрезке $[-7; 3]$, дробь $\frac{6}{(x + 5)^2 + 1}$ всегда положительна, а значит, $f(x)$ будет положительным или равным нулю.
• График будет положительным на отрезке $[-7; 3]$, а за его пределами, при $x \to -\infty$, будет стремиться к $-3$.

Как построить:

1. Вычисляйте $f(x)$ для значений $x$ на интервале $[-7, 3]$.
2. Для $x$ меньших, чем -7, вычисляйте $f(x)$ и наблюдайте, как оно стремится к -3.
3. График будет иметь форму функции с горбом, где он будет положительным на $[-7, 3]$, а затем плавно снижаться и приближаться к -3.

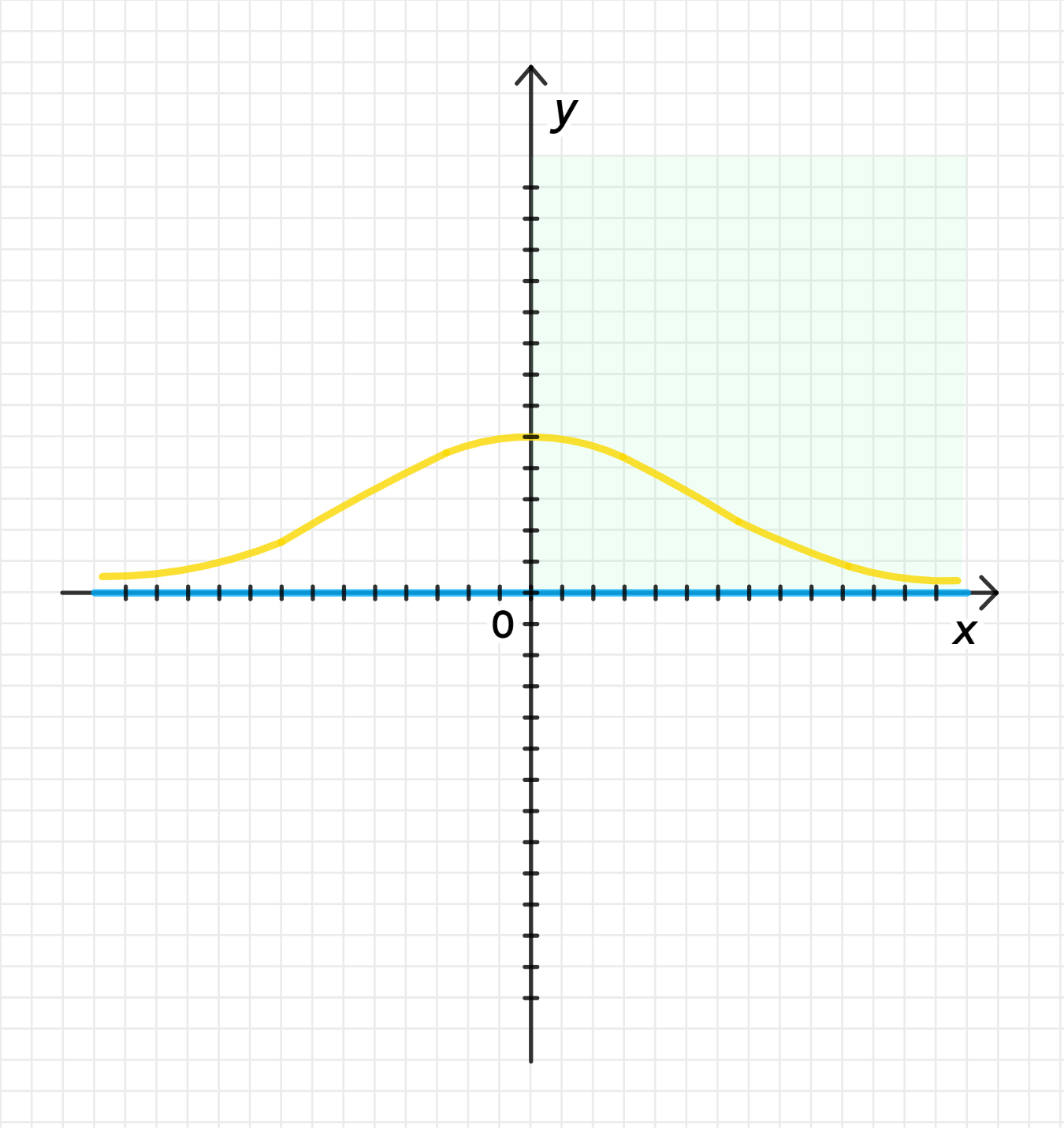
в)

Функция: $\lim_{x \to \infty} f(x) = 0$ и $f(x) > 0$ на $[0; +∞)$.

Для этого условия подходит функция:

$$f(x) = \frac{1}{x^2 + 1}$$

Шаги построения:

• При $x \to \infty$, дробь $\frac{1}{x^2 + 1}$ стремится к 0.
• При $x = 0$, $f(0) = 1$, а затем для $x > 0$ функция быстро убывает, стремясь к 0.
• График всегда будет положительным, так как знаменатель $x^2 + 1$ всегда больше 0.

Как построить:

1. Для разных значений $x \geq 0$ вычисляйте значения функции $f(x)$.
2. Наблюдайте, как функция $f(x)$ быстро убывает с увеличением $x$.
3. График будет представлять собой кривую, которая начинается с 1 при $x = 0$ и постепенно приближается к 0, но никогда не достигает его.

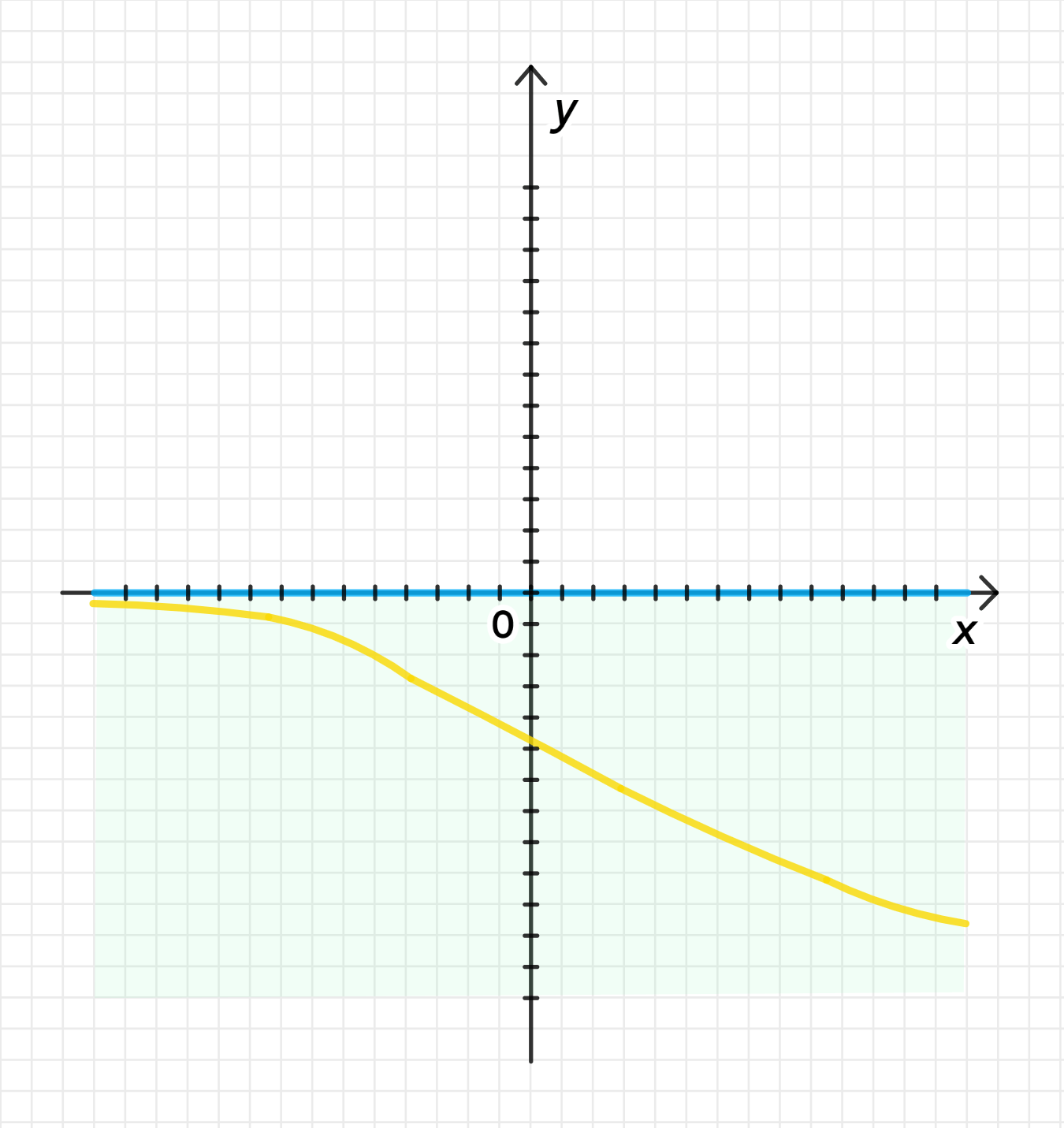
г)

Функция: $\lim_{x \to -\infty} f(x) = 0$ и $f(x) < 0$ на $(-∞; +∞)$.

Для этого подходит функция:

$$f(x) = -\frac{1}{x^2 + 1}$$

Шаги построения:

• При $x \to -\infty$, функция стремится к 0.
• Функция всегда отрицательна, так как $\frac{1}{x^2 + 1}$ положительна, но знак минус делает её отрицательной на всей числовой прямой.
• График будет асимптотично приближаться к 0, но всегда оставаться ниже оси абсцисс.

Как построить:

1. Для разных значений $x$ вычисляйте $f(x)$.
2. Отметьте точки на графике, чтобы увидеть, как функция постепенно приближается к 0, оставаясь всегда отрицательной.
3. График будет представлять собой плавно спадающую кривую, которая никогда не пересекает ось $x$ и стремится к 0, но всегда ниже этой оси.