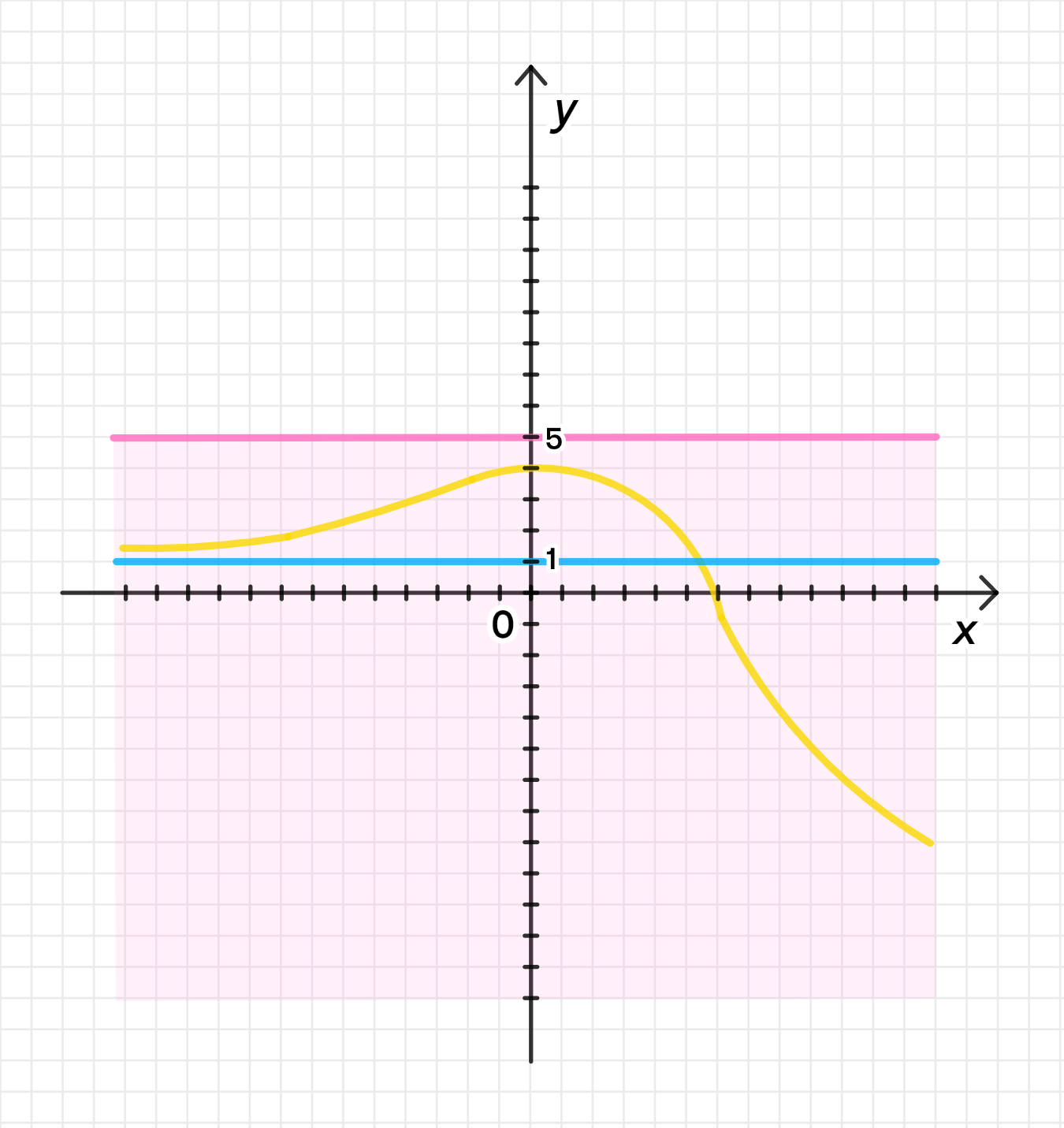Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 39.9 Профильный Уровень Мордкович — Подробные Ответы
Постройте график какой-нибудь функции у = h(x), х € R обладающей указанными свойствами:
а) и функция ограничена сверху
б) и функция ограничена снизу
в) и функция ограничена сверху
г) и функция ограничена снизу
а) и функция ограничена сверху:
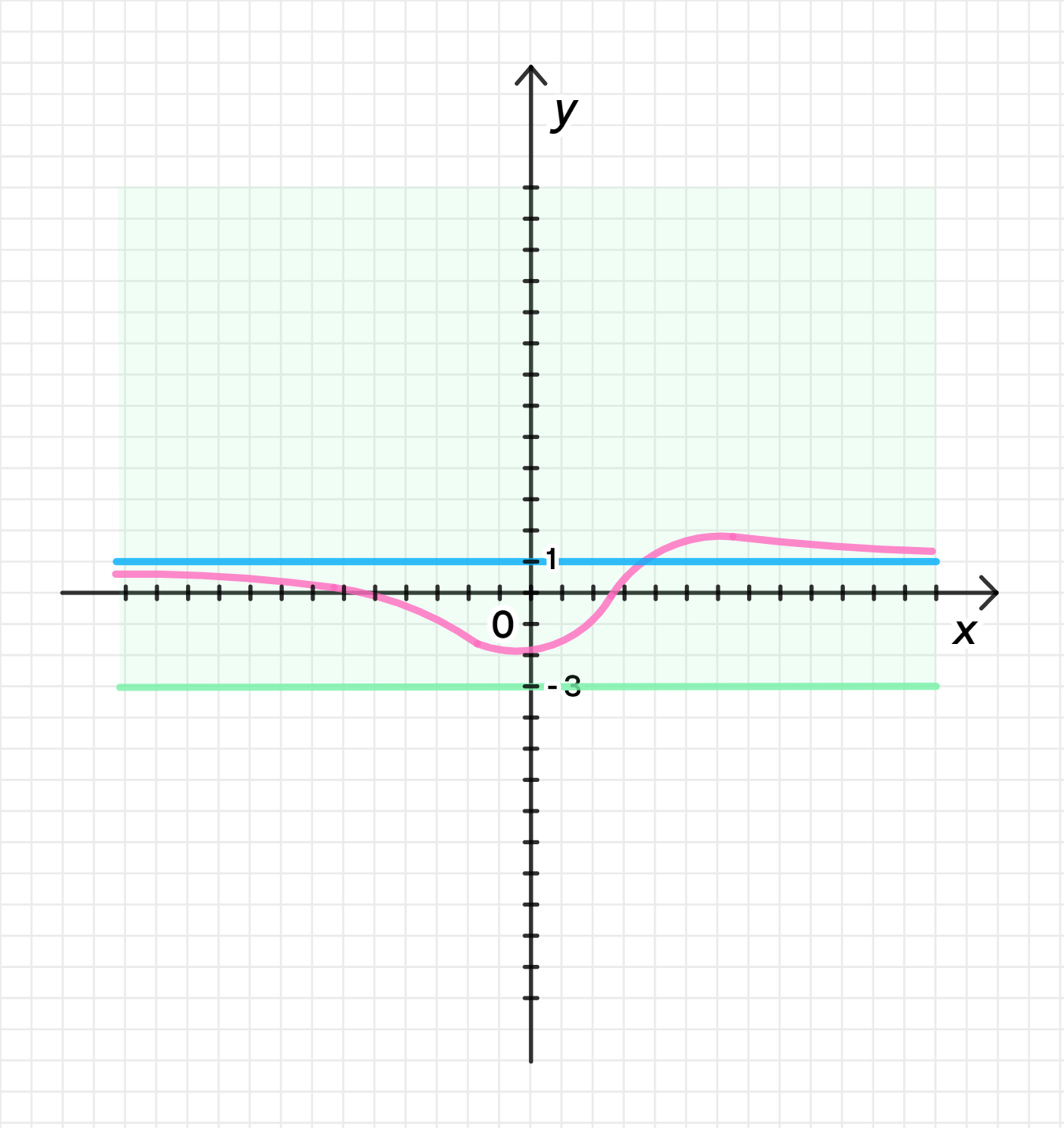
б) и функция ограничена снизу:
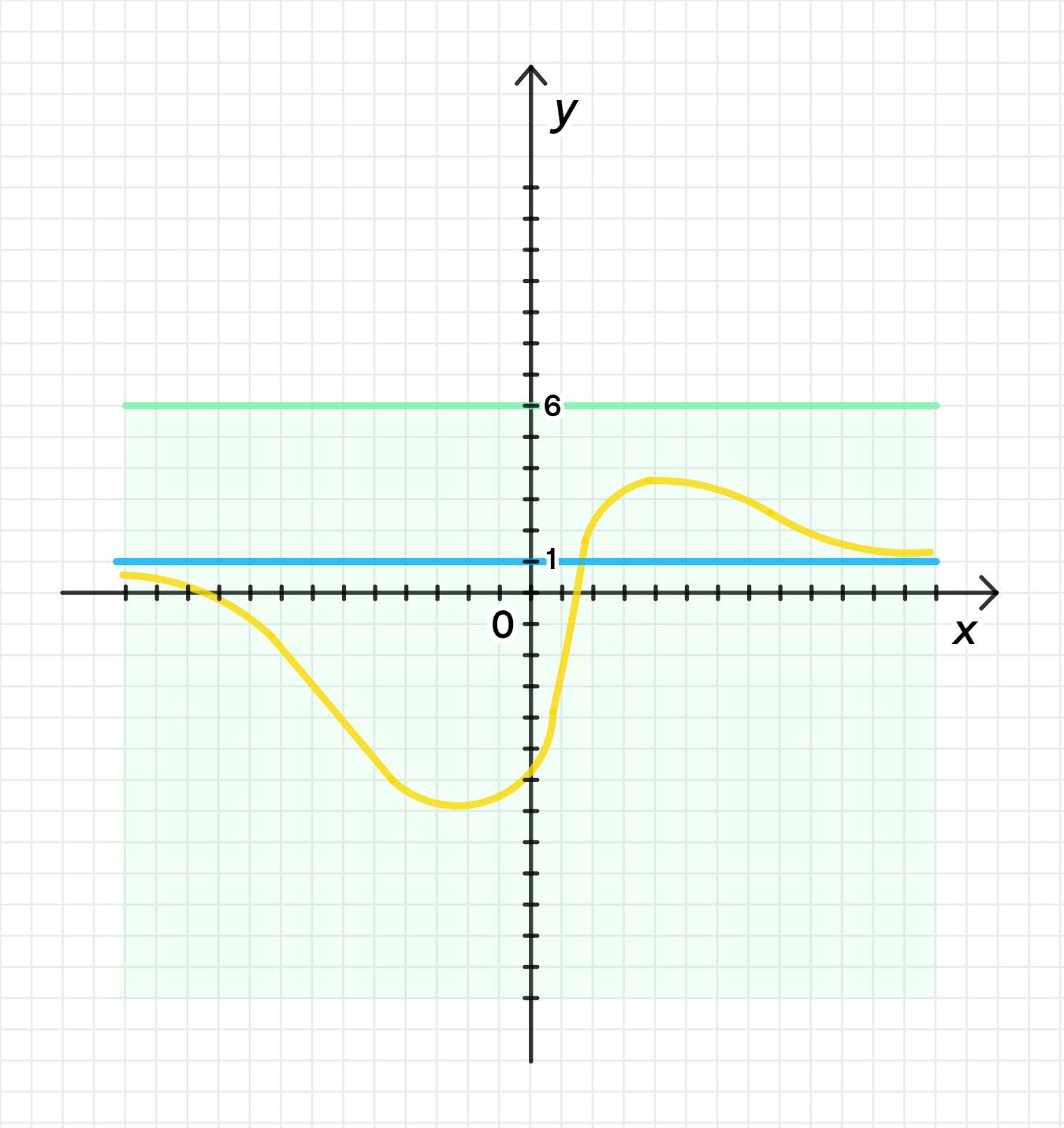
в) и функция ограничена сверху:
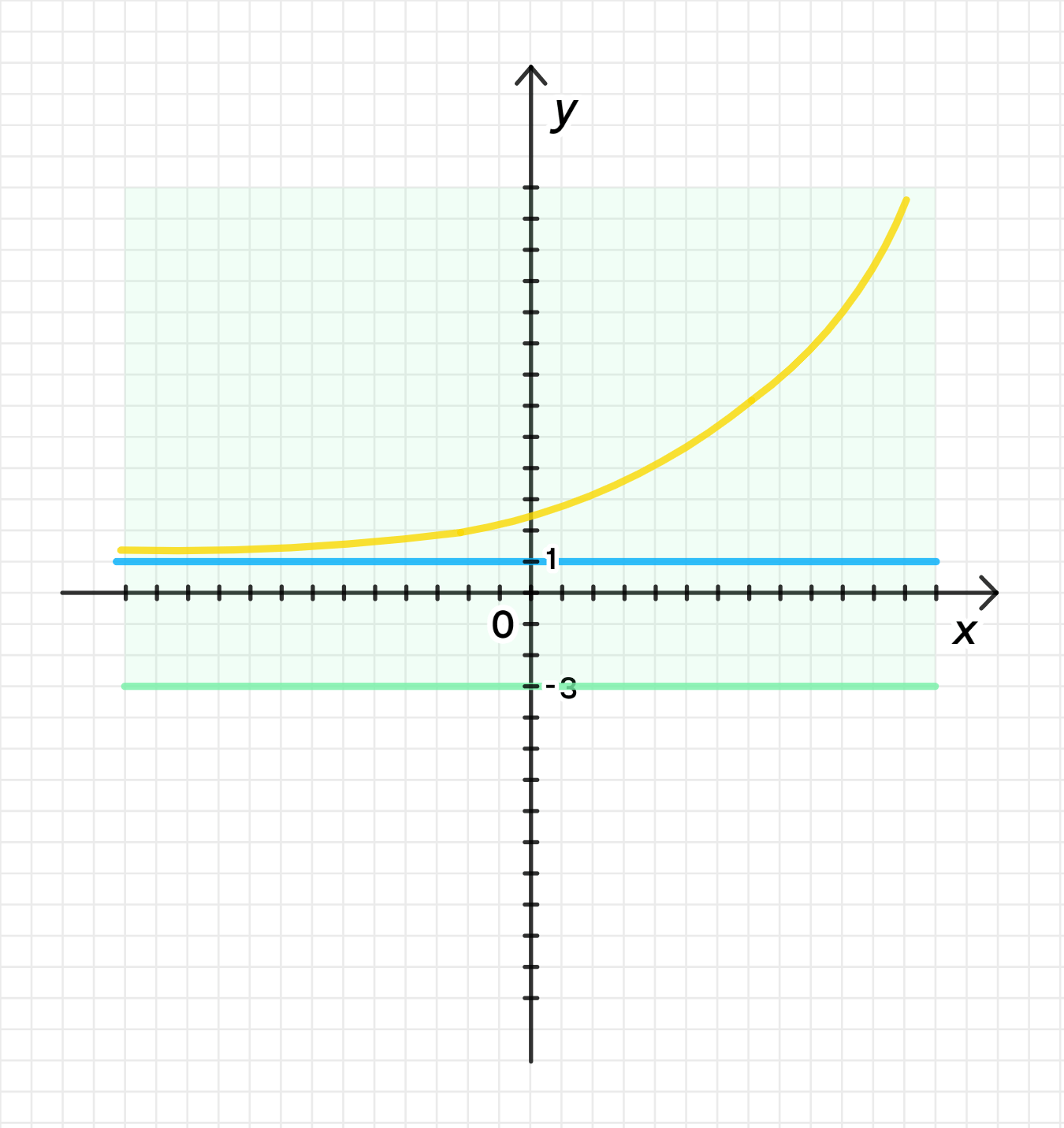
г) и функция ограничена снизу:
а)
Функция: и функция ограничена сверху.
Нам нужно найти функцию, которая:
- Стремится к 1, когда .
- Ограничена сверху, то есть у неё есть верхняя граница (она не растет бесконечно).
Предположим, подходящей функцией будет:
Почему эта функция подходит?
- Когда , , и функция .
- Функция ограничена сверху, так как для всех выполняется . Это видно, потому что , и таким образом, .
Шаги построения графика:
- Вычисляйте значения функции для разных значений , например, от до .
- Наблюдайте, как функция приближается к 1 при .
- График будет иметь форму гиперболы, которая снижается, приближаясь к 1, но не пересекает её. Функция ограничена сверху значением 2.
б)
Функция: и функция ограничена снизу.
Нам нужна функция, которая:
- Стремится к 1, когда .
- Ограничена снизу, то есть у неё есть нижняя граница (она не убывает бесконечно).
Предположим, подходящей функцией будет:
Почему эта функция подходит?
- Когда , , и функция .
- Функция ограничена снизу, так как для всех выполняется . Это видно, потому что , и таким образом, .
Шаги построения графика:
- Вычисляйте значения функции для разных значений , например, от до .
- Наблюдайте, как функция приближается к 1 при .
- График будет представлять собой кривую, которая начинает с положительных значений и постепенно приближается к 1, но не пересекает её, оставаясь выше 0.
в)
Функция: и функция ограничена сверху.
Это условие аналогично условию (а), так что функция будет такой же:
Почему эта функция подходит?
- Когда , , и функция .
- Функция ограничена сверху значением 2, как объяснялось ранее.
Шаги построения графика:
- Для значений от до вычисляйте значения .
- Наблюдайте, как функция приближается к 1, но всегда остается ниже 2.
- График будет асимптотически стремиться к 1, но не пересечет её, ограничиваясь сверху значением 2.
г)
Функция: и функция ограничена снизу.
Нам нужно выбрать функцию, которая:
- Стремится к 1, когда .
- Ограничена снизу, то есть её значения не убывают до минус бесконечности.
Предположим, подходящей функцией будет:
Почему эта функция подходит?
- Когда , , и .
- Функция ограничена снизу значением 0, так как , и таким образом, .
Шаги построения графика:
- Для значений от до вычисляйте .
- Наблюдайте, как функция приближается к 1 при .
- График будет плавно возрастать, приближаясь к 1, но не пересекает её, оставаясь выше 0.
Общие шаги для построения графика:
- Выберите подходящую функцию из предложенных.
- Определите диапазон значений , например, от до или от до , в зависимости от того, как далеко вы хотите видеть поведение функции.
- Вычисляйте значения функции для различных .
- Построите график на основе вычисленных значений, используя оси и .
- Наблюдайте, как функция ведет себя на больших и малых значениях , стремясь к пределам, и как она ограничена сверху или снизу.