ГДЗ по Алгебре 10 Класс Номер 4.12 Профильный Уровень Мордкович — Подробные Ответы

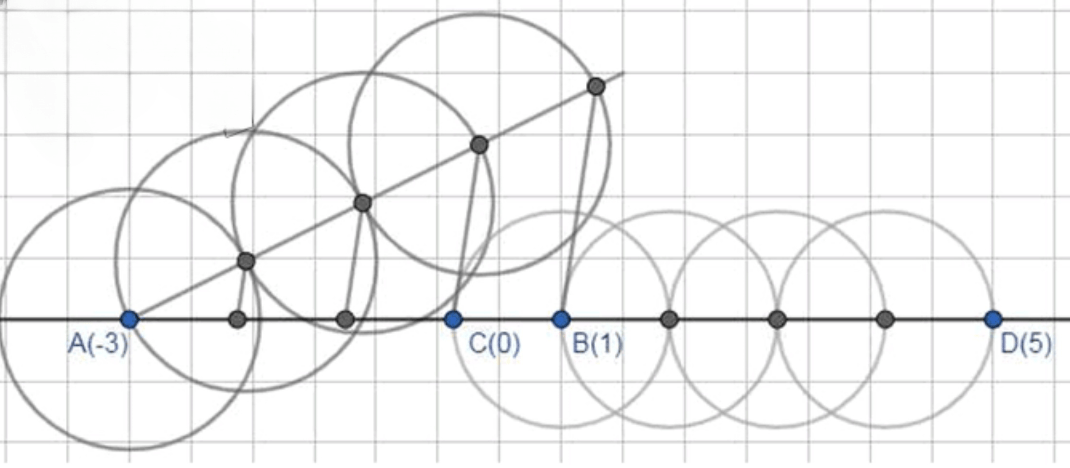
а) На числовой прямой отмечены точки $-3$ и $1$. При помощи циркуля и линейки постройте точки $0$ и $5$.

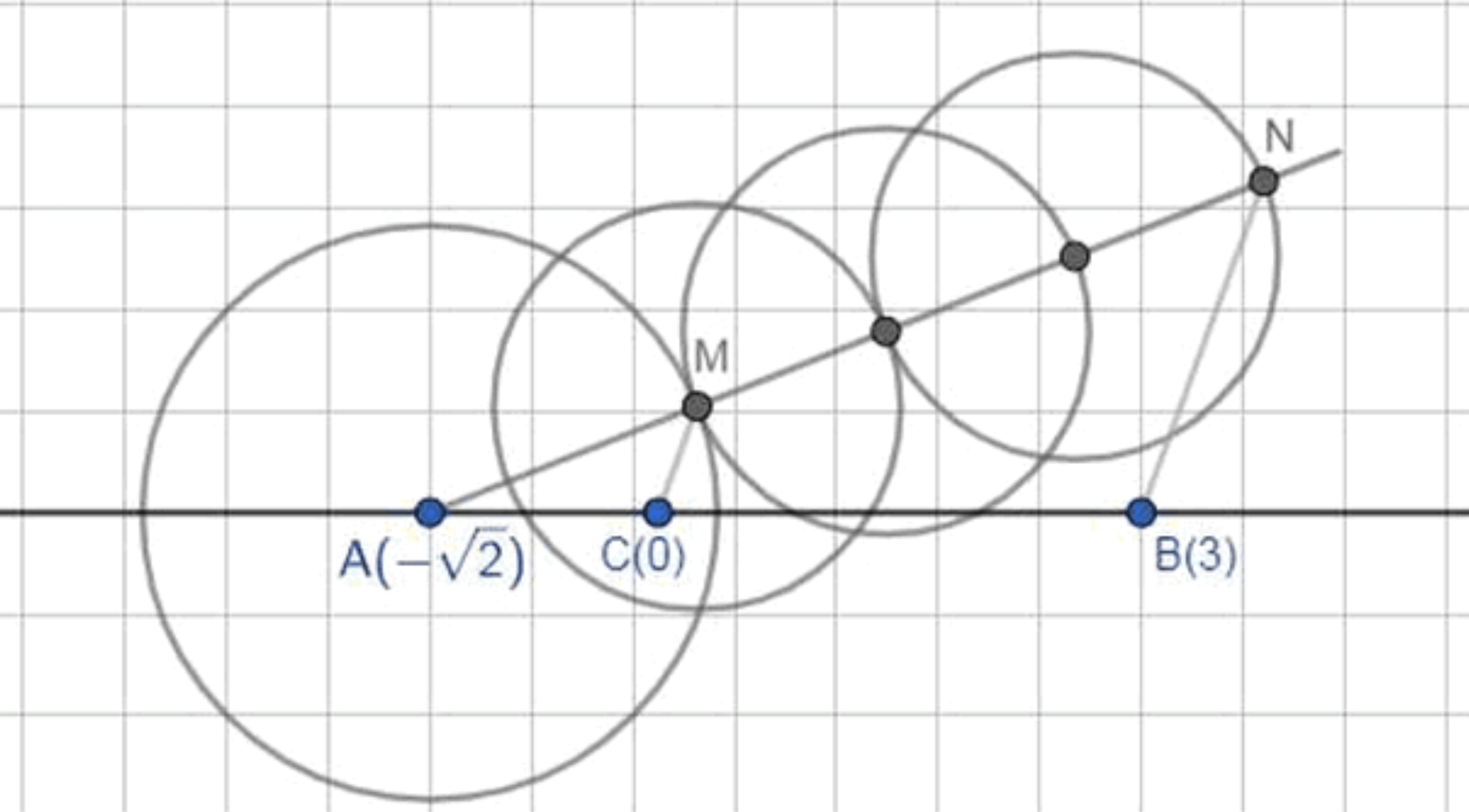
б) На числовой прямой отмечены точки $-\sqrt{2}$ и $3$. При помощи циркуля и линейки постройте точку $0$.

а) На числовой прямой отмечены точки $A(-3)$ и $B(1)$, требуется отметить точки $C(0)$ и $D(5)$ при помощи циркуля и линейки;

1. Разделим отрезок $AB$ на четыре равные части, для чего:

• Проведем из точки $A$ произвольный луч;
• Отложим последовательно на этом луче 4 равных отрезка;
• От конца последнего отрезка проведем прямую через точку $B$;
• Через концы других отрезков проведем параллельные ей прямые;

2. Каждый из этих отрезков является единичным:

$$l = \frac{AB}{4} = \frac{1 — (-3)}{4} = \frac{1 + 3}{4} = \frac{4}{4} = 1;$$

3. От точки $B(1)$ отложим один единичный отрезок влево и четыре единичных отрезка вправо:

б) На числовой прямой отмечены точки $A(-\sqrt{2})$ и $B(3)$, требуется отметить точку $C(0)$;

1. Возьмем произвольный единичный отрезок;

2. Построим прямоугольный треугольник с катетами:

$$a = 1 \quad \text{и} \quad b = 1;$$ $$c = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2};$$

3. Проведем из точки $A(-\sqrt{2})$ произвольный луч;

4. На этом луче отложим отрезок $AM$ длины $\sqrt{2}$;

5. Отложим на луче от точки $M$ последовательно три единичных отрезка, конец последнего из них обозначим буквой $N$;

6. Проведем прямую $NB$ и параллельную ей прямую $MC$, которая пересечет числовую прямую в точке $C(0)$:

7. По теореме о пропорциональных отрезках:

$$\frac{AC}{CB} = \frac{AM}{MN} = \frac{\sqrt{2}}{3};$$

Часть а)

Задание: На числовой прямой отмечены точки $A(-3)$ и $B(1)$, требуется отметить точки $C(0)$ и $D(5)$ при помощи циркуля и линейки.

Шаг 1: Разделение отрезка $AB$ на 4 равные части

Определим длину отрезка $AB$:

• Точки $A$ и $B$ имеют координаты $A(-3)$ и $B(1)$.
• Длина отрезка $AB$ вычисляется как разность координат $B$ и $A$:

  $$AB = 1 — (-3) = 1 + 3 = 4.$$

• Длина отрезка $AB$ равна 4 единицам.

Разделим отрезок $AB$ на 4 равные части:

• Для того чтобы разделить отрезок $AB$ на 4 равные части, нужно длину отрезка $AB$ (равную 4) разделить на 4:

  $$l = \frac{AB}{4} = \frac{4}{4} = 1.$$

• Каждая из частей будет длиной 1 единица.

Построим разделение:

• Проведем из точки $A$ произвольный луч, который будет использоваться для отложения равных отрезков.
• С помощью циркуля отложим 4 равных отрезка длиной 1.
• Отложив 4 равных отрезка, получим точки, разделяющие отрезок $AB$ на 4 части.
• После этого, используя линейку, соединяем последнюю точку с точкой $B(1)$.
• Параллельно этой прямой через другие точки проведем прямые, которые также будут разделять отрезок $AB$ на равные части.

Шаг 2: Длины отрезков

Каждый из этих отрезков будет иметь длину:

$$l = \frac{AB}{4} = 1.$$

Таким образом, длина каждого отрезка разделяющего $AB$ на 4 части, равна 1.

Шаг 3: Отложение единичных отрезков от точки $B$

От точки $B(1)$ отложим 1 единичный отрезок влево.

• Для этого мы отложим отрезок длиной 1 единица влево от точки $B$. Точка, которая будет находиться на расстоянии 1 единица влево от точки $B(1)$, будет точкой с координатой $0$.

Отложим 4 единичных отрезка вправо.

• Теперь, от точки $B(1)$ откладываем 4 отрезка длиной 1 единица вправо. Это приведет к тому, что мы получим точку $D(5)$ с координатой 5.

Часть б)

Задание: На числовой прямой отмечены точки $A(-\sqrt{2})$ и $B(3)$, требуется отметить точку $C(0)$.

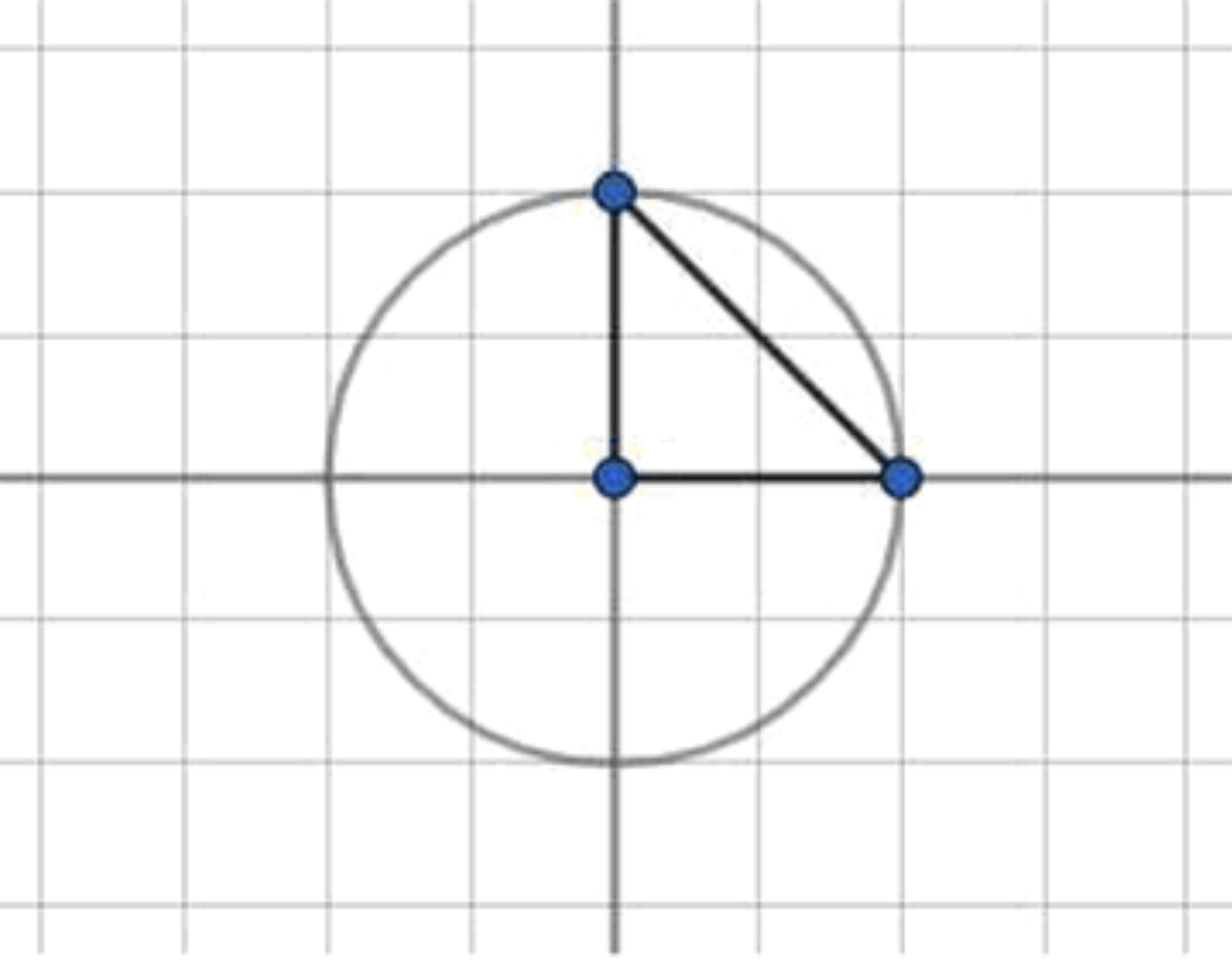
Шаг 1: Построение прямоугольного треугольника с катетами

Построим прямоугольный треугольник с катетами:

• Нам нужно построить прямоугольный треугольник с катетами длины 1, чтобы найти гипотенузу.
• По теореме Пифагора длина гипотенузы $c$ равна:

  $$c = \sqrt{1^2 + 1^2} = \sqrt{2}.$$

• Таким образом, гипотенуза будет иметь длину $\sqrt{2}$.

Шаг 2: Откладывание отрезка длины $\sqrt{2}$

Отложим отрезок длины $\sqrt{2}$ вправо от точки $A(-\sqrt{2})$.

• На числовой прямой точка $A$ имеет координату $-\sqrt{2}$, и отложив от этой точки отрезок длины $\sqrt{2}$, мы получим точку $M$ с координатой 0, так как:

  $$A(-\sqrt{2}) + \sqrt{2} = 0.$$

• Это точка $C(0)$.

Шаг 3: Отложение единичных отрезков

Отложим на луче от точки $M$ 3 единичных отрезка.

• От точки $M(0)$ отложим 3 единичных отрезка длиной 1, и конечная точка будет точкой $N$, которая будет находиться на координате 3.

Шаг 4: Прямая через точки $N$ и $B$

Проводим прямую $NB$.

• Теперь проведем прямую через точку $N$ и точку $B(3)$, которая будет проходить через обе эти точки.

Проводим параллельную прямую $MC$.

• Параллельно прямой $NB$ проводим прямую через точку $M(0)$, и эта прямая пересечет числовую прямую в точке $C(0)$.

Шаг 5: Применение теоремы о пропорциональных отрезках

По теореме о пропорциональных отрезках:

$$\frac{AC}{CB} = \frac{AM}{MN} = \frac{\sqrt{2}}{3}.$$