Краткий ответ:
а) y = ∣ x − 2 ∣ ( x − 2 ) y = |x — 2|(x — 2) x 0 = 2 x_0 = 2
По определению модуля числа:
y = { − ( x − 2 ) 2 , если x < 2 ; ( x − 2 ) 2 , если x ≥ 2 ; y = \begin{cases} -(x — 2)^2, & \text{если } x < 2; \\ (x — 2)^2, & \text{если } x \geq 2; \end{cases}
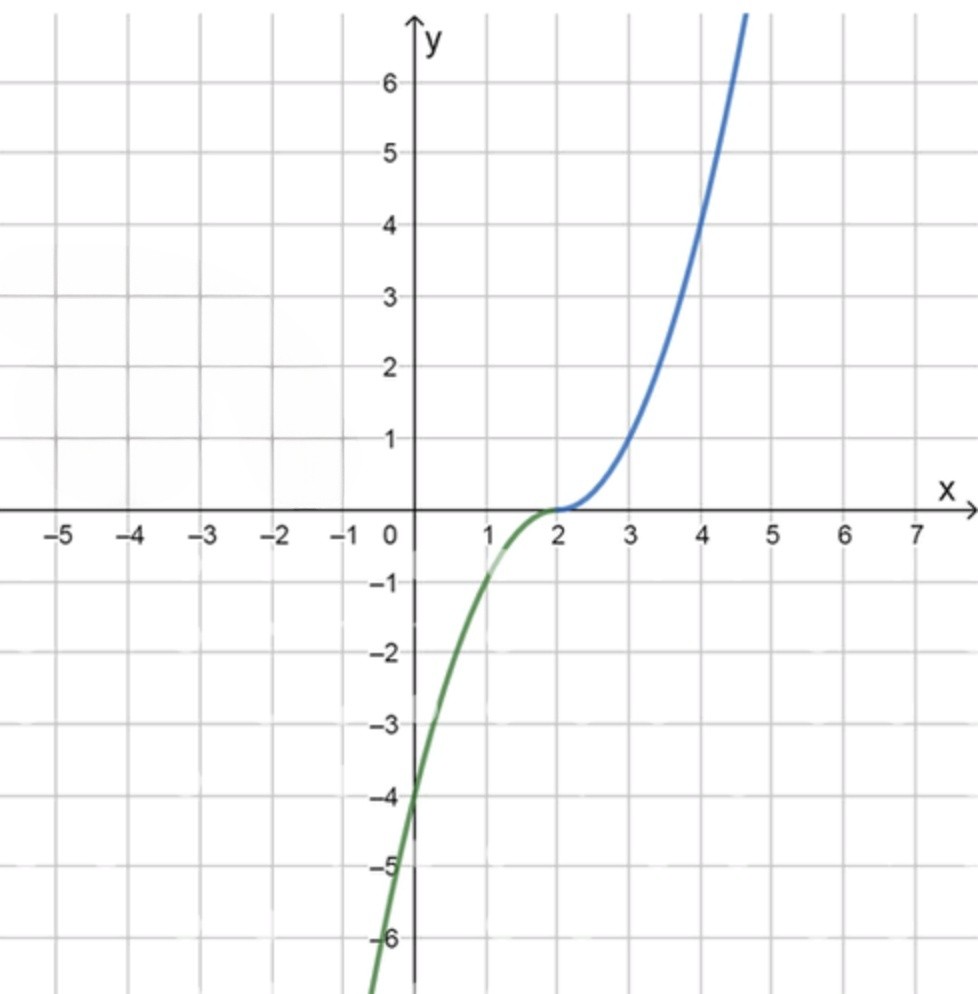
График функции:
x 0 1 2 3 4 y − 4 − 1 0 1 4 \begin{array}{c|c|c|c|c|c} x & 0 & 1 & 2 & 3 & 4 \\ \hline y & -4 & -1 & 0 & 1 & 4 \\ \end{array}
Искомая точка принадлежит функции:
y = ( x − 2 ) 2 = x 2 − 4 x + 4 ; y = (x — 2)^2 = x^2 — 4x + 4;
Значение производной:
y ′ = ( x 2 ) ′ − ( 4 x + 4 ) ′ = 2 x − 4 ; y’ = (x^2)’ — (4x + 4)’ = 2x — 4; y ′ ( x 0 ) = 2 ⋅ 2 − 4 = 4 − 4 = 0 ; y'(x_0) = 2 \cdot 2 — 4 = 4 — 4 = 0;
Ответ: y ′ = 0 y’ = 0
б) y = ( x + 2 ) ∣ x + 2 ∣ y = (x + 2)|x + 2| x 0 = − 2 x_0 = -2
По определению модуля числа:
y = { − ( x + 2 ) 2 , если x < − 2 ; ( x + 2 ) 2 , если x ≥ − 2 ; y = \begin{cases} -(x + 2)^2, & \text{если } x < -2; \\ (x + 2)^2, & \text{если } x \geq -2; \end{cases}
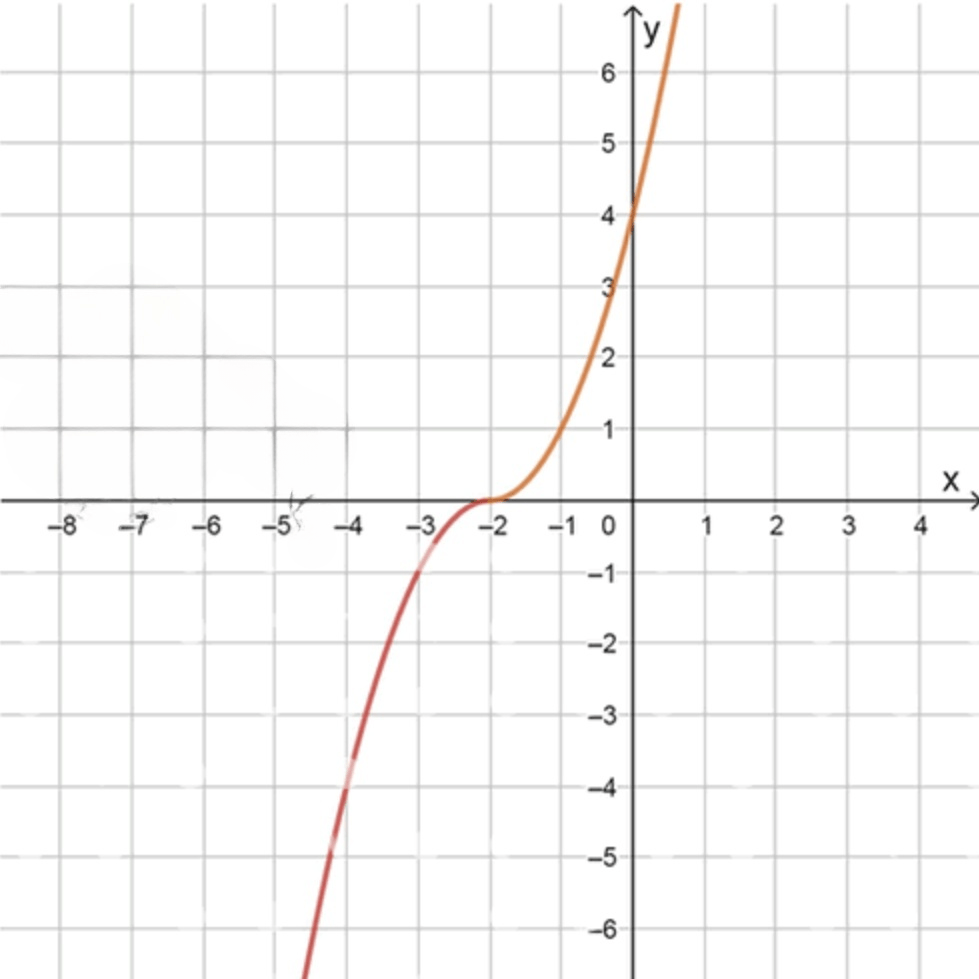
График функции:
x − 4 − 3 − 2 − 1 0 y − 4 − 1 0 1 4 \begin{array}{c|c|c|c|c|c} x & -4 & -3 & -2 & -1 & 0 \\ \hline y & -4 & -1 & 0 & 1 & 4 \\ \end{array}
Искомая точка принадлежит функции:
y = ( x + 2 ) 2 = x 2 + 4 x + 4 ; y = (x + 2)^2 = x^2 + 4x + 4;
Значение производной:
y ′ = ( x 2 ) ′ + ( 4 x + 4 ) ′ = 2 x + 4 ; y’ = (x^2)’ + (4x + 4)’ = 2x + 4; y ′ ( x 0 ) = 2 ⋅ ( − 2 ) + 4 = − 4 + 4 = 0 ; y'(x_0) = 2 \cdot (-2) + 4 = -4 + 4 = 0;
Ответ: y ′ = 0 y’ = 0
Подробный ответ:
а) y = ∣ x − 2 ∣ ( x − 2 ) y = |x — 2|(x — 2) x 0 = 2 x_0 = 2
Шаг 1. Раскрываем модуль по определению
Функция содержит модуль: ∣ x − 2 ∣ |x — 2|
∣ x − 2 ∣ = { − ( x − 2 ) , если x < 2 ; x − 2 , если x ≥ 2. |x — 2| = \begin{cases} -(x — 2), & \text{если } x < 2; \\ x — 2, & \text{если } x \geq 2. \end{cases}
Подставим это в функцию:
y = ∣ x − 2 ∣ ( x − 2 ) = { − ( x − 2 ) ( x − 2 ) , x < 2 ; ( x − 2 ) ( x − 2 ) , x ≥ 2 ; y = |x — 2|(x — 2) = \begin{cases} -(x — 2)(x — 2), & x < 2; \\ (x — 2)(x — 2), & x \geq 2; \end{cases}
Упростим:
y = { − ( x − 2 ) 2 , x < 2 ; ( x − 2 ) 2 , x ≥ 2. y = \begin{cases} -(x — 2)^2, & x < 2; \\ (x — 2)^2, & x \geq 2. \end{cases}
Шаг 2. Таблица значений функции
Подставим несколько значений x x y y
| x x y = ∣ x − 2 ∣ ( x − 2 ) y = |x — 2|(x — 2) 0 0 ∣ 0 − 2 ∣ ⋅ ( 0 − 2 ) = 2 ⋅ ( − 2 ) = − 4 |0 — 2| \cdot (0 — 2) = 2 \cdot (-2) = -4 1 1 ∣ 1 − 2 ∣ ⋅ ( 1 − 2 ) = 1 ⋅ ( − 1 ) = − 1 |1 — 2| \cdot (1 — 2) = 1 \cdot (-1) = -1 2 2 ∣ 2 − 2 ∣ ⋅ ( 2 − 2 ) = 0 ⋅ 0 = 0 |2 — 2| \cdot (2 — 2) = 0 \cdot 0 = 0 3 3 ∣ 3 − 2 ∣ ⋅ ( 3 − 2 ) = 1 ⋅ 1 = 1 |3 — 2| \cdot (3 — 2) = 1 \cdot 1 = 1 4 4 ∣ 4 − 2 ∣ ⋅ ( 4 − 2 ) = 2 ⋅ 2 = 4 |4 — 2| \cdot (4 — 2) = 2 \cdot 2 = 4
Итоговая таблица:
x 0 1 2 3 4 y − 4 − 1 0 1 4 \begin{array}{c|c|c|c|c|c} x & 0 & 1 & 2 & 3 & 4 \\ \hline y & -4 & -1 & 0 & 1 & 4 \\ \end{array}
Шаг 3. Уточняем выражение на отрезке, включающем x 0 = 2 x_0 = 2
Так как x 0 = 2 x_0 = 2 x ≥ 2 x \geq 2
y = ( x − 2 ) 2 = x 2 − 4 x + 4. y = (x — 2)^2 = x^2 — 4x + 4.
Это и будет функция, которой принадлежит точка x = 2 x = 2
Шаг 4. Находим производную y ′ y’
Найдём производную от:
y = x 2 − 4 x + 4. y = x^2 — 4x + 4.
Дифференцируем по правилам:
Производная от x 2 x^2 2 x 2x Производная от − 4 x -4x − 4 -4 Производная от константы 4 4 0 0 Итак:
y ′ = 2 x − 4. y’ = 2x — 4.
Шаг 5. Подставим x 0 = 2 x_0 = 2
y ′ ( x 0 ) = y ′ ( 2 ) = 2 ⋅ 2 − 4 = 4 − 4 = 0. y'(x_0) = y'(2) = 2 \cdot 2 — 4 = 4 — 4 = 0.
Ответ :
y ′ = 0 \boxed{y’ = 0}
б) y = ( x + 2 ) ∣ x + 2 ∣ y = (x + 2)|x + 2| x 0 = − 2 x_0 = -2
Шаг 1. Раскрываем модуль по определению
Рассмотрим модуль ∣ x + 2 ∣ |x + 2|
∣ x + 2 ∣ = { − ( x + 2 ) , x < − 2 ; x + 2 , x ≥ − 2. |x + 2| = \begin{cases} -(x + 2), & x < -2; \\ x + 2, & x \geq -2. \end{cases}
Тогда функция:
y = ( x + 2 ) ∣ x + 2 ∣ = { ( x + 2 ) ( − ( x + 2 ) ) = − ( x + 2 ) 2 , x < − 2 ; ( x + 2 ) ( x + 2 ) = ( x + 2 ) 2 , x ≥ − 2. y = (x + 2)|x + 2| = \begin{cases} (x + 2)(-(x + 2)) = -(x + 2)^2, & x < -2; \\ (x + 2)(x + 2) = (x + 2)^2, & x \geq -2. \end{cases}
Шаг 2. Таблица значений
Подставим значения x x
| x x y = ( x + 2 ) ∣ x + 2 ∣ y = (x + 2)|x + 2| − 4 -4 ( − 2 ) ∣ − 2 ∣ = − 2 ⋅ 2 = − 4 (-2)|-2| = -2 \cdot 2 = -4 − 3 -3 ( − 1 ) ∣ − 1 ∣ = − 1 ⋅ 1 = − 1 (-1)|-1| = -1 \cdot 1 = -1 − 2 -2 0 ⋅ 0 = 0 0 \cdot 0 = 0 − 1 -1 1 ⋅ 1 = 1 1 \cdot 1 = 1 0 0 2 ⋅ 2 = 4 2 \cdot 2 = 4
Итоговая таблица:
x − 4 − 3 − 2 − 1 0 y − 4 − 1 0 1 4 \begin{array}{c|c|c|c|c|c} x & -4 & -3 & -2 & -1 & 0 \\ \hline y & -4 & -1 & 0 & 1 & 4 \\ \end{array}
Шаг 3. Найдём явное выражение для x 0 = − 2 x_0 = -2
Так как x 0 = − 2 x_0 = -2 x ≥ − 2 x \geq -2
y = ( x + 2 ) 2 = x 2 + 4 x + 4. y = (x + 2)^2 = x^2 + 4x + 4.
Шаг 4. Найдём производную
Функция:
y = x 2 + 4 x + 4. y = x^2 + 4x + 4.
Дифференцируем:
( x 2 ) ′ = 2 x (x^2)’ = 2x ( 4 x ) ′ = 4 (4x)’ = 4 ( 4 ) ′ = 0 (4)’ = 0 Итого:
y ′ = 2 x + 4. y’ = 2x + 4.
Шаг 5. Подставим x 0 = − 2 x_0 = -2
y ′ ( x 0 ) = y ′ ( − 2 ) = 2 ⋅ ( − 2 ) + 4 = − 4 + 4 = 0. y'(x_0) = y'(-2) = 2 \cdot (-2) + 4 = -4 + 4 = 0.
Ответ :
y ′ = 0 \boxed{y’ = 0}