ГДЗ по Алгебре 10 Класс Номер 43.69 Профильный Уровень Мордкович — Подробные Ответы

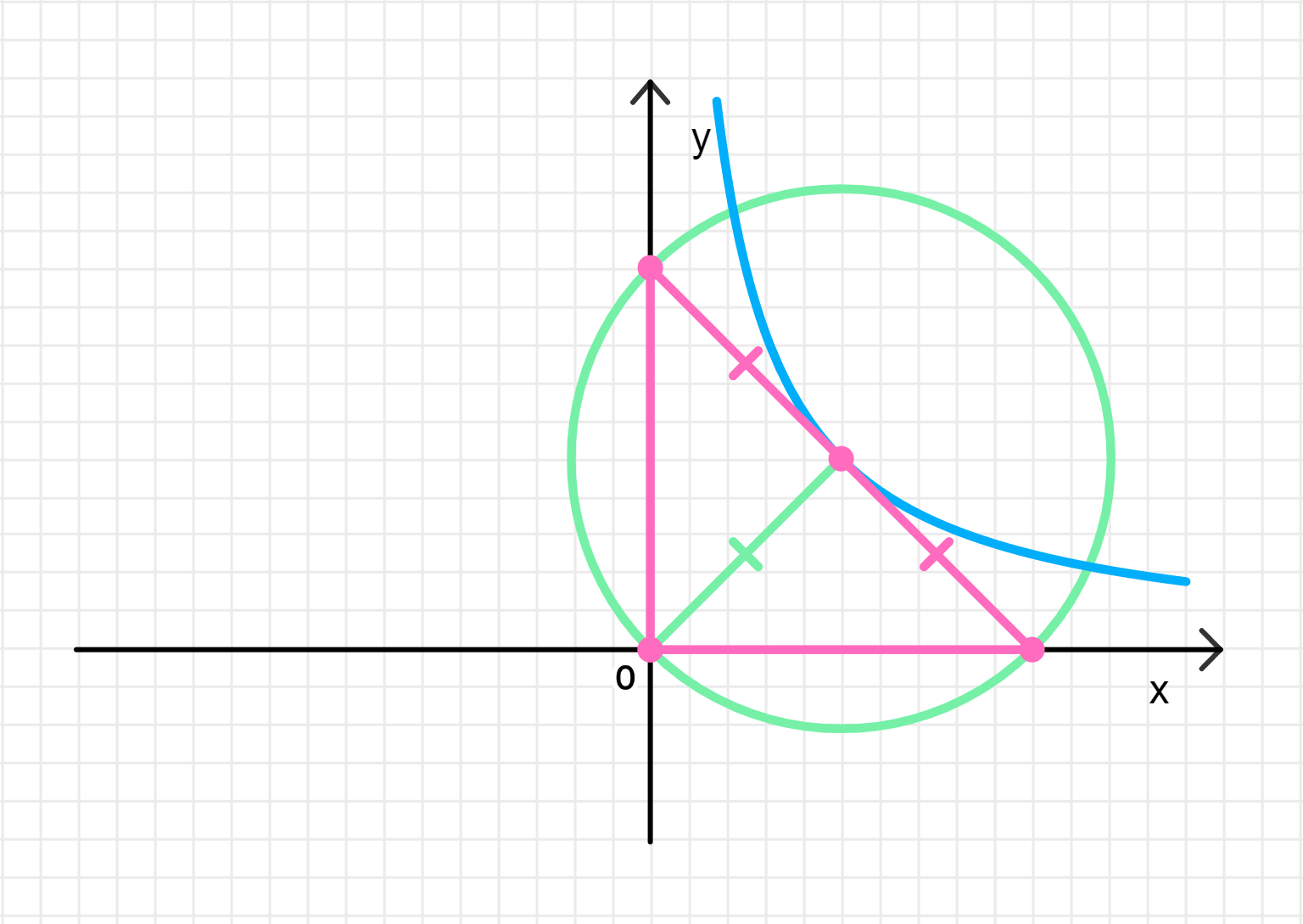
Докажите, что треугольник, образованный касательной к гиперболе $y = \frac{a^2}{x}$ и осями координат, имеет постоянную площадь, а точка касания является центром окружности, описанной около этого треугольника. Рассмотрев чертёж к задаче, придумайте геометрический способ построения касательной к гиперболе.

Отрезки, которые касательная отсекает от осей координат, являются катетами искомого треугольника;

Дана функция: $f(x) = \frac{a^2}{x}$;

Пусть $b$ — абсцисса точки касания;

I. Докажем, что такой треугольник имеет постоянную площадь:

Уравнение касательной:

$$f(b) = \frac{a^2}{b};$$ $$f'(b) = a^2 \cdot \left( \frac{1}{x} \right)’ = -\frac{a^2}{x^2} = -\frac{a^2}{b^2};$$ $$y = \frac{a^2}{b} — \frac{a^2}{b^2}(x — b) = \frac{a^2 b}{b^2} — \frac{a^2 x}{b^2} + \frac{a^2 b}{b^2} = \frac{a^2}{b^2}(2b — x);$$

Абсцисса пересечения касательной с осью $x$:

$$\frac{a^2}{b^2}(2b — x) = 0;$$ $$a^2(2b — x) = 0;$$ $$2b — x = 0, \text{ отсюда } x = 2b;$$

Ордината пересечения касательной с осью $y$:

$$y(0) = \frac{a^2}{b^2}(2b — 0) = \frac{2a^2 b}{b^2} = \frac{2a^2}{b};$$

Площадь отсекаемого треугольника:

$$S = \frac{1}{2} \cdot |x| \cdot |y| = \frac{1}{2} \cdot |2b| \cdot \left| \frac{2a^2}{b} \right| = 2a^2;$$

Таким образом, площадь постоянна, что и требовалось доказать.

II. Докажем, что точка касания является центром описанной окружности:

Длина гипотенузы — расстояние между точками $(2b; 0)$ и $\left( 0; \frac{2a^2}{b} \right)$:

$$c = \sqrt{(2b)^2 + \left( \frac{2a^2}{b} \right)^2} = \sqrt{\frac{4b^4 + 4a^4}{b^2}} = \frac{2}{b} \sqrt{b^4 + a^4}$$

Расстояние от точки касания $\left( b; \frac{a^2}{b} \right)$ до точки $(2b; 0)$:

$$d = \sqrt{(b — 2b)^2 + \left( \frac{a^2}{b} \right)^2} = \sqrt{\frac{b^4 + a^4}{b^2}} = \frac{1}{b} \sqrt{b^4 + a^4};$$

Отношение данных величин:

$$\frac{d}{c} = \frac{1}{b} \sqrt{b^4 + a^4} : \frac{2}{b} \sqrt{b^4 + a^4} = \frac{1}{b} \cdot \frac{b}{2} = \frac{1}{2};$$

Таким образом, точка касания является серединой гипотенузы искомого треугольника, следовательно она является серединой описанной около него окружности, что и требовалось доказать.

III. Рассмотрим чертеж к задаче:

1. Точка касания является серединой гипотенузы, следовательно расстояние от этой точки до начала координат (вершины прямого угла) равно половине расстояния между точками пересечения касательной с осями координат;
2. Таким образом, для построения касательной к гиперболе достаточно провести из точки касания окружность, проходящую через начало координат, тогда касательная будет проходить через точку пересечения этой окружности с осями координат.

Докажите, что треугольник, образованный касательной к гиперболе

$$y = \frac{a^2}{x}$$

и осями координат, имеет постоянную площадь, а точка касания является центром описанной окружности этого треугольника.
Также, рассмотрев чертёж, найдите геометрический способ построения касательной к гиперболе.

I. Докажем, что площадь треугольника постоянна

Шаг 1: Задание функции

Гипербола дана как

$$f(x) = \frac{a^2}{x}$$

где $a$ — фиксированное положительное число.

Пусть касательная проведена к гиперболе в точке с абсциссой $x = b$.
Тогда точка касания имеет координаты:

$$(b, f(b)) = \left(b, \frac{a^2}{b}\right)$$

Шаг 2: Найдём производную функции

Поскольку касательная — это прямая, касающаяся графика функции в данной точке, её наклон (угловой коэффициент) равен значению производной функции в точке касания.

Функция:

$$f(x) = \frac{a^2}{x} = a^2 \cdot x^{-1}$$

Производная:

$$f'(x) = a^2 \cdot (-1) \cdot x^{-2} = -\frac{a^2}{x^2}$$

Подставим $x = b$:

$$f'(b) = -\frac{a^2}{b^2}$$

Шаг 3: Уравнение касательной в точке $(b, \frac{a^2}{b})$

Общий вид уравнения касательной:

$$y = f(b) + f'(b)(x — b)$$

Подставим значения:

$$y = \frac{a^2}{b} — \frac{a^2}{b^2}(x — b)$$

Раскроем скобки:

$$y = \frac{a^2}{b} — \frac{a^2 x}{b^2} + \frac{a^2 b}{b^2}$$

Сложим подобные:

$$y = \frac{a^2}{b^2}(2b — x)$$

Шаг 4: Найдём пересечения касательной с осями координат

Пересечение с осью OX (y = 0):

Подставим $y = 0$ в уравнение касательной:

$$\frac{a^2}{b^2}(2b — x) = 0 \Rightarrow 2b — x = 0 \Rightarrow x = 2b$$

Таким образом, точка пересечения касательной с осью $x$:

$$(2b, 0)$$

Пересечение с осью OY (x = 0):

Подставим $x = 0$:

$$y = \frac{a^2}{b^2}(2b — 0) = \frac{2a^2 b}{b^2} = \frac{2a^2}{b}$$

Точка пересечения с осью $y$:

$$\left(0, \frac{2a^2}{b}\right)$$

Шаг 5: Найдём площадь треугольника

Треугольник ограничен:

• Осью $x$: основание — от 0 до $2b$
• Осью $y$: высота — от 0 до $\frac{2a^2}{b}$
• Касательной — гипотенуза

Площадь треугольника:

$$S = \frac{1}{2} \cdot \text{основание} \cdot \text{высота} = \frac{1}{2} \cdot 2b \cdot \frac{2a^2}{b}$$

Упростим:

$$S = \frac{1}{2} \cdot \frac{4a^2 b}{b} = 2a^2$$

Вывод:
Площадь $S = 2a^2$ не зависит от точки касания (не зависит от $b$),
значит, она постоянна.

II. Докажем, что точка касания — центр описанной окружности

Шаг 1: Найдём длину гипотенузы

Гипотенуза соединяет точки:

• $(2b, 0)$
• $\left(0, \frac{2a^2}{b}\right)$

По формуле расстояния между точками:

$$c = \sqrt{(2b — 0)^2 + \left(0 — \frac{2a^2}{b}\right)^2} = \sqrt{4b^2 + \frac{4a^4}{b^2}}$$

Приведём к общему знаменателю:

$$c = \sqrt{ \frac{4b^4 + 4a^4}{b^2} } = \frac{2}{b} \sqrt{b^4 + a^4}$$

Шаг 2: Найдём расстояние от точки касания до конца гипотенузы

Точка касания:

$$\left(b, \frac{a^2}{b}\right)$$

До точки $(2b, 0)$:

$$d = \sqrt{(b — 2b)^2 + \left(\frac{a^2}{b}\right)^2} = \sqrt{b^2 + \frac{a^4}{b^2}} = \sqrt{\frac{b^4 + a^4}{b^2}} = \frac{1}{b} \sqrt{b^4 + a^4}$$

Шаг 3: Сравним длину отрезка с половиной гипотенузы

$$\frac{d}{c} = \frac{ \frac{1}{b} \sqrt{b^4 + a^4} }{ \frac{2}{b} \sqrt{b^4 + a^4} } = \frac{1}{2}$$

Вывод:
Точка касания находится на середине гипотенузы ⇒
Это центр описанной окружности прямоугольного треугольника
(в прямоугольном треугольнике окружность описывается вокруг середины гипотенузы).

III. Геометрический способ построения касательной

Шаг 1: Заметим, что точка касания — центр описанной окружности

Из предыдущего пункта мы знаем, что если мы знаем точку касания,
то она является серединой отрезка, соединяющего пересечения касательной с осями координат.

Шаг 2: Центр описанной окружности лежит на одинаковом расстоянии от всех вершин треугольника

Поскольку одна вершина треугольника — начало координат $(0, 0)$,
а другая — точка касания,
можно построить окружность с центром в точке касания,
проходящую через $(0, 0)$.

Шаг 3: Касательная пересечёт оси координат в двух других точках окружности

• Построим окружность с центром в точке касания и радиусом, равным расстоянию до начала координат.
• Эта окружность пересечёт оси $x$ и $y$ в точках, где и будет пересекать касательная.
• Проведём прямую через эти две точки — это и будет касательная.

Итог:

1. Площадь треугольника, образованного касательной и осями, равна $2a^2$ и не зависит от точки касания.
2. Точка касания — это центр описанной окружности вокруг треугольника.
3. Геометрический способ построения касательной:
   постройте окружность с центром в предполагаемой точке касания,
   проходящую через начало координат.
   Касательная — это прямая, соединяющая точки пересечения этой окружности с осями координат.