ГДЗ по Алгебре 10 Класс Номер 43.70 Профильный Уровень Мордкович — Подробные Ответы

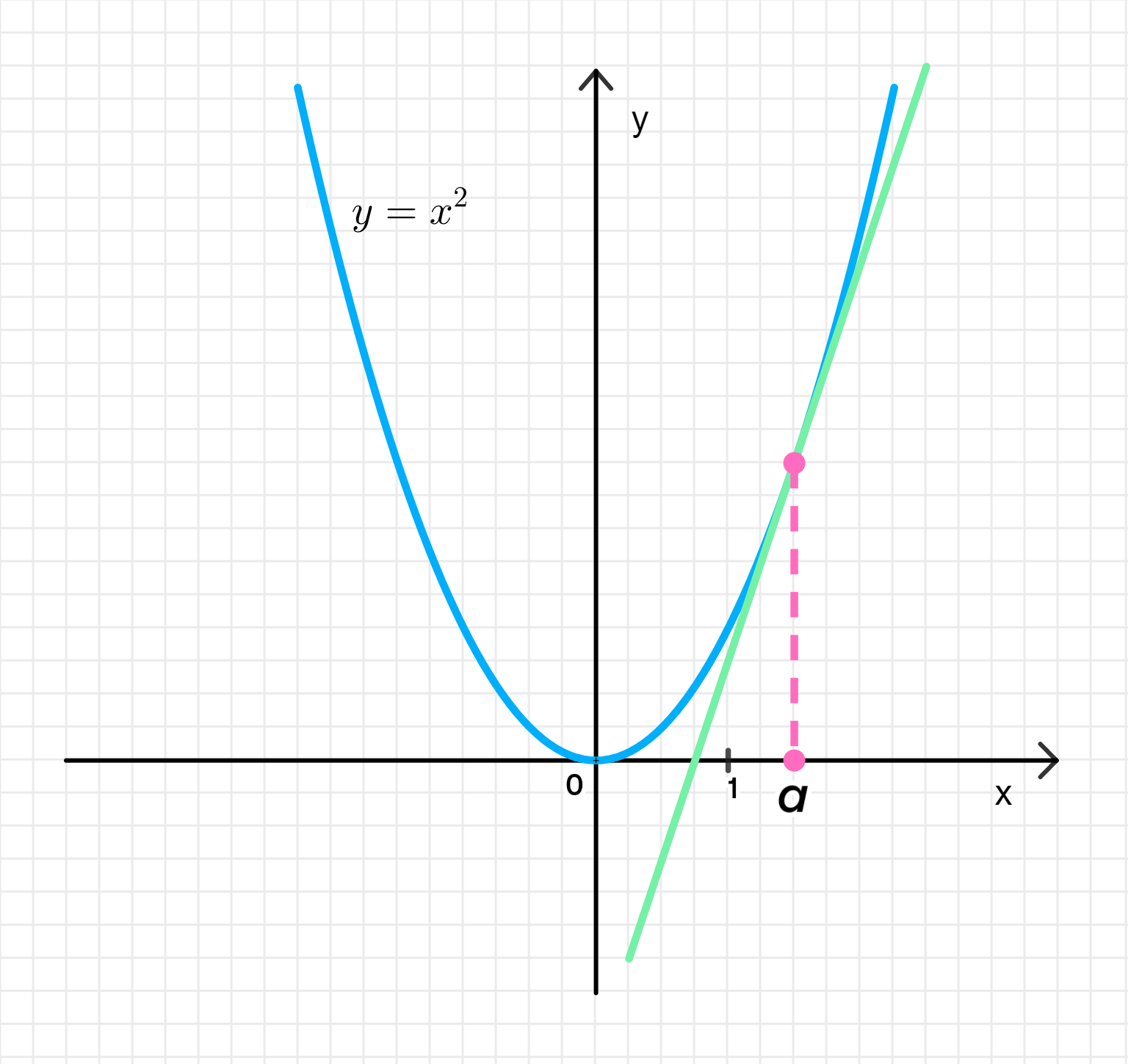
Докажите, что касательная к параболе $y = x^2$ в точке $x = a$ делит пополам отрезок $[0; a]$ оси абсцисс. Рассмотрев чертёж к задаче, придумайте геометрический способ построения касательной к параболе. Обобщите этот результат и этот способ построения касательной на любую степенную функцию $y = x^n$, где $n$ — натуральное число, большее 2.

Дана функция: $f(x) = x^2$ и $x = a$ — точка касания;

I. Докажем, что касательная делит пополам отрезок $[0; a]$ оси $x$:

Уравнение касательной:

$$f(a) = a^2;$$ $$f'(a) = (x^2)’ = 2x = 2a;$$ $$y = a^2 + 2a(x — a) = a^2 + 2ax — 2a^2 = 2ax — a^2;$$

Абсцисса пересечения касательной с осью $x$:

$$2ax — a^2 = 0;$$ $$2ax = a^2, \text{отсюда } x = \frac{a^2}{2a} = \frac{a}{2};$$

Таким образом, касательная делит отрезок $[0; a]$ пополам, что и требовалось доказать.

II. Рассмотрим чертеж к задаче:

Таким образом, для построения касательной к параболе достаточно опустить перпендикуляр из точки касания на ось абсцисс, тогда касательная будет проходить через середину отрезка, заключенного между основанием этого перпендикуляра и началом координат;

III. Рассмотрим функцию $f(x) = x^n$, где $n > 2$ и $n \in \mathbb{N}$:

Уравнение касательной:

$$f(a) = a^n;$$ $$f'(a) = (x^n)’ = nx^{n-1} = na^{n-1} = \frac{na^n}{a};$$ $$y = a^n + \frac{na^n}{a}(x — a) = a^n + \frac{nxa^n}{a} — na^n;$$

Абсцисса пересечения касательной с осью $x$:

$$a^n + \frac{nxa^n}{a} — na^n = 0;$$ $$\frac{na^n}{a} \cdot x = na^n — a^n;$$ $$x = \frac{a(na^n — a^n)}{na^n} = \frac{a \cdot na^n — a \cdot a^n}{na^n} = a — \frac{a}{n};$$

Таким образом, касательная к функции $f(x) = x^n$ в точке $a$ отсекает от отрезка $[0; a]$ часть, равную $\frac{1}{n}$ длины этого отрезка, считая от точки с абсциссой $a$;

Для построения касательной к данной функции достаточно опустить перпендикуляр из точки касания на ось абсцисс, тогда касательная будет проходить внутри отрезка через точку, удаленную на $\frac{a}{n}$ от точки с абсциссой $a$.

Дана функция $f(x) = x^2$, и точка касания $x = a$.
Нужно:

1. Доказать, что касательная к графику функции в этой точке делит пополам отрезок $[0; a]$ на оси $x$;
2. Предложить геометрический способ построения касательной по рисунку;
3. Обобщить результат и способ на степенную функцию $f(x) = x^n$, где $n \in \mathbb{N},\ n > 2$.

I. Доказательство: касательная к параболе $y = x^2$ в точке $x = a$

Шаг 1. Найдём значение функции в точке $x = a$

Функция дана:

$$f(x) = x^2$$

Значит, в точке $x = a$:

$$f(a) = a^2$$

Это координата точки касания по оси $y$:
точка касания имеет координаты $(a, a^2)$

Шаг 2. Найдём производную $f'(x)$

Производная:

$$f'(x) = \frac{d}{dx}(x^2) = 2x$$

Подставляем $x = a$:

$$f'(a) = 2a$$

Это — угловой коэффициент касательной к графику в точке $x = a$.

Шаг 3. Уравнение касательной

Уравнение касательной к функции в точке $x = a$ с производной $f'(a)$ и значением функции $f(a)$ даётся формулой:

$$y = f(a) + f'(a)(x — a)$$

Подставляем:

$$y = a^2 + 2a(x — a)$$

Раскрываем скобки:

$$y = a^2 + 2ax — 2a^2 = 2ax — a^2$$

Итак, уравнение касательной:

$$y = 2ax — a^2$$

Шаг 4. Найдём точку пересечения касательной с осью $x$

Чтобы найти пересечение с осью абсцисс, приравниваем $y = 0$:

$$2ax — a^2 = 0$$

Решаем это уравнение:

Переносим $a^2$ в другую сторону:

$$2ax = a^2$$

Делим обе части на $2a$ (предполагая $a \ne 0$):

$$x = \frac{a^2}{2a} = \frac{a}{2}$$

Шаг 5. Что это значит геометрически?

Касательная к параболе $y = x^2$ в точке $x = a$ пересекает ось $x$ в точке:

$$x = \frac{a}{2}$$

То есть точно посередине отрезка от $0$ до $a$, так как:

$$\frac{0 + a}{2} = \frac{a}{2}$$

Вывод:

Касательная делит отрезок $[0; a]$ ровно пополам, что и требовалось доказать.

II. Геометрический способ построения касательной

Шаг 1. Рассматриваем чертёж

На графике изображена парабола $y = x^2$, точка касания $A(a, a^2)$, и проведена касательная.

Шаг 2. Что видно на чертеже?

• Из точки $A$ можно опустить перпендикуляр на ось абсцисс — он попадёт в точку $(a, 0)$
• Касательная проходит через точку с абсциссой $\frac{a}{2}$ на оси $x$

Шаг 3. Геометрическое построение

1. Отложить точку $A = (a, a^2)$ на параболе
2. Опустить из неё перпендикуляр на ось $x$, получить точку $(a, 0)$
3. Построить отрезок от начала координат $(0, 0)$ до точки $(a, 0)$
4. Найти середину этого отрезка: точка $\left( \frac{a}{2}, 0 \right)$
5. Провести прямую через точки $A = (a, a^2)$ и $\left( \frac{a}{2}, 0 \right)$

Это и будет касательная к параболе в точке $A$

III. Обобщение на функцию $f(x) = x^n$, $n > 2,\ n \in \mathbb{N}$

Шаг 1. Дано: функция $f(x) = x^n$, точка касания $x = a$

Точка касания:

$$f(a) = a^n$$

Шаг 2. Производная функции

$$f'(x) = \frac{d}{dx}(x^n) = nx^{n — 1}$$

Подставим $x = a$:

$$f'(a) = na^{n-1}$$

Шаг 3. Уравнение касательной

По формуле:

$$y = f(a) + f'(a)(x — a)$$

Подставляем:

$$y = a^n + na^{n-1}(x — a)$$

Раскрываем:

$$y = a^n + na^{n-1}x — na^n = na^{n-1}x — (n — 1)a^n$$

Шаг 4. Найдём пересечение касательной с осью $x$

При $y = 0$:

$$na^{n-1}x — (n — 1)a^n = 0$$

Решаем:

$$na^{n-1}x = (n — 1)a^n$$

Делим обе части на $na^{n-1}$:

$$x = \frac{(n — 1)a^n}{na^{n-1}} = \frac{(n — 1)a}{n}$$

Шаг 5. Геометрический смысл

Отрезок по оси $x$ от $0$ до $a$: длина $a$
Касательная пересекает ось $x$ в точке:

$$x = \left(1 — \frac{1}{n}\right)a$$

То есть она отсекает отрезок длины $\frac{a}{n}$ от точки $a$

Шаг 6. Геометрический способ построения

1. Находим точку $A = (a, a^n)$ на графике
2. Опускаем из неё перпендикуляр на ось $x$, получаем точку $(a, 0)$
3. Отрезок от $x = a$ до $x = 0$ имеет длину $a$
4. Откладываем от точки $x = a$ влево отрезок длины $\frac{a}{n}$, получаем точку:

   $$x = a — \frac{a}{n} = \left(1 — \frac{1}{n}\right)a$$

5. Проводим прямую через точки $A$ и $\left( \left(1 — \frac{1}{n} \right) a,\ 0 \right)$

Это будет касательная к функции $y = x^n$ в точке $x = a$

Вывод:

• Для функции $y = x^2$ касательная делит отрезок $[0; a]$ пополам
• Для $y = x^n$, $n > 2$, она делит отрезок $[0; a]$ в отношении $\frac{1}{n} : \frac{n — 1}{n}$, считая от точки $x = a$
• Геометрически касательную можно построить через точку касания и точку на оси $x$, удалённую на $\frac{a}{n}$ от $a$