ГДЗ по Алгебре 10 Класс Номер 44.29 Профильный Уровень Мордкович — Подробные Ответы

а) $f(x) = x^3 — 3x + 2$;
$f'(x) = (x^3)’ — (3x — 2)’ = 3x^2 — 3$;

Промежуток возрастания:
$3x^2 — 3 \geq 0$;
$x^2 — 1 \geq 0$;
$x^2 \geq 1$, отсюда $x \leq -1$ или $x \geq 1$;

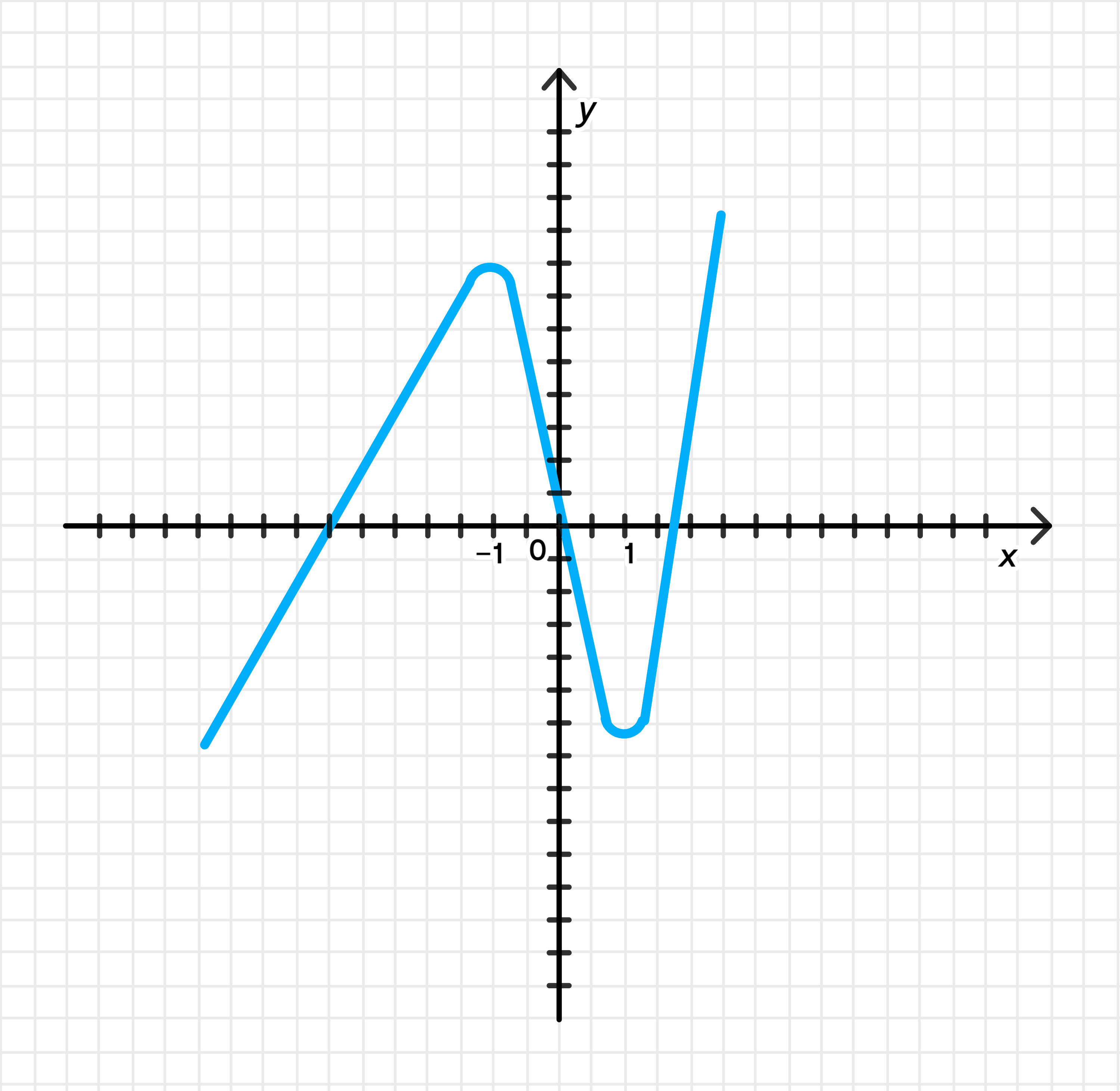
Схематичный график:

Ответ: возрастает на $(-\infty; -1] \cup [1; +\infty)$ и убывает на $[-1; 1]$.

б) $f(x) = x^4 — 2x^2 + 1$;
$f'(x) = (x^4)’ — 2(x^2)’ + (1)’ = 4x^3 — 2 \cdot 2x + 0 = 4x^3 — 4x$;

Промежуток возрастания:
$4x^3 — 4x \geq 0$;
$x^3 — x \geq 0$;
$x(x^2 — 1) \geq 0$;
$(x + 1) \cdot x \cdot (x — 1) \geq 0$;
$-1 \leq x \leq 0$ или $x \geq 1$;

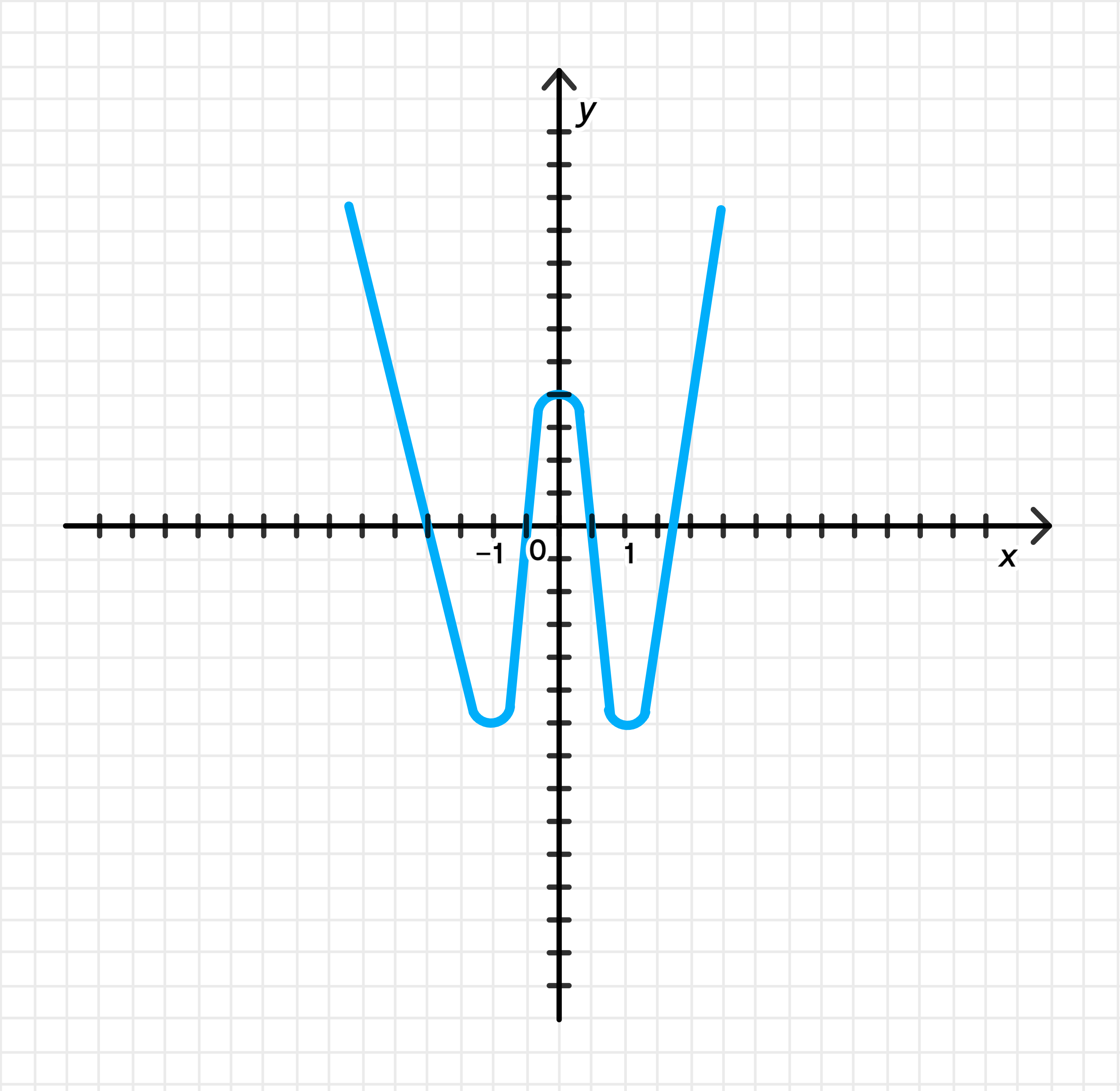
Схематичный график:

Ответ: возрастает на $[-1; 0] \cup [1; +\infty)$ и убывает на $(-\infty; -1] \cup [0; 1]$.

в) $f(x) = x^3 + 6x^2 — 15x + 8$;
$f'(x) = (x^3)’ + 6(x^2)’ — (15x — 8)’ = 3x^2 + 6 \cdot 2x — 15 = 3x^2 + 12x — 15$;

Промежуток возрастания:
$3x^2 + 12x — 15 = 0$;
$x^2 + 4x — 5 = 0$;
$D = 4^2 + 4 \cdot 5 = 16 + 20 = 36$, тогда:
$x_1 = \frac{-4 — 6}{2} = -5$ и $x_2 = \frac{-4 + 6}{2} = 1$;
$(x + 5)(x — 1) \geq 0$;
$x \leq -5$ или $x \geq 1$;

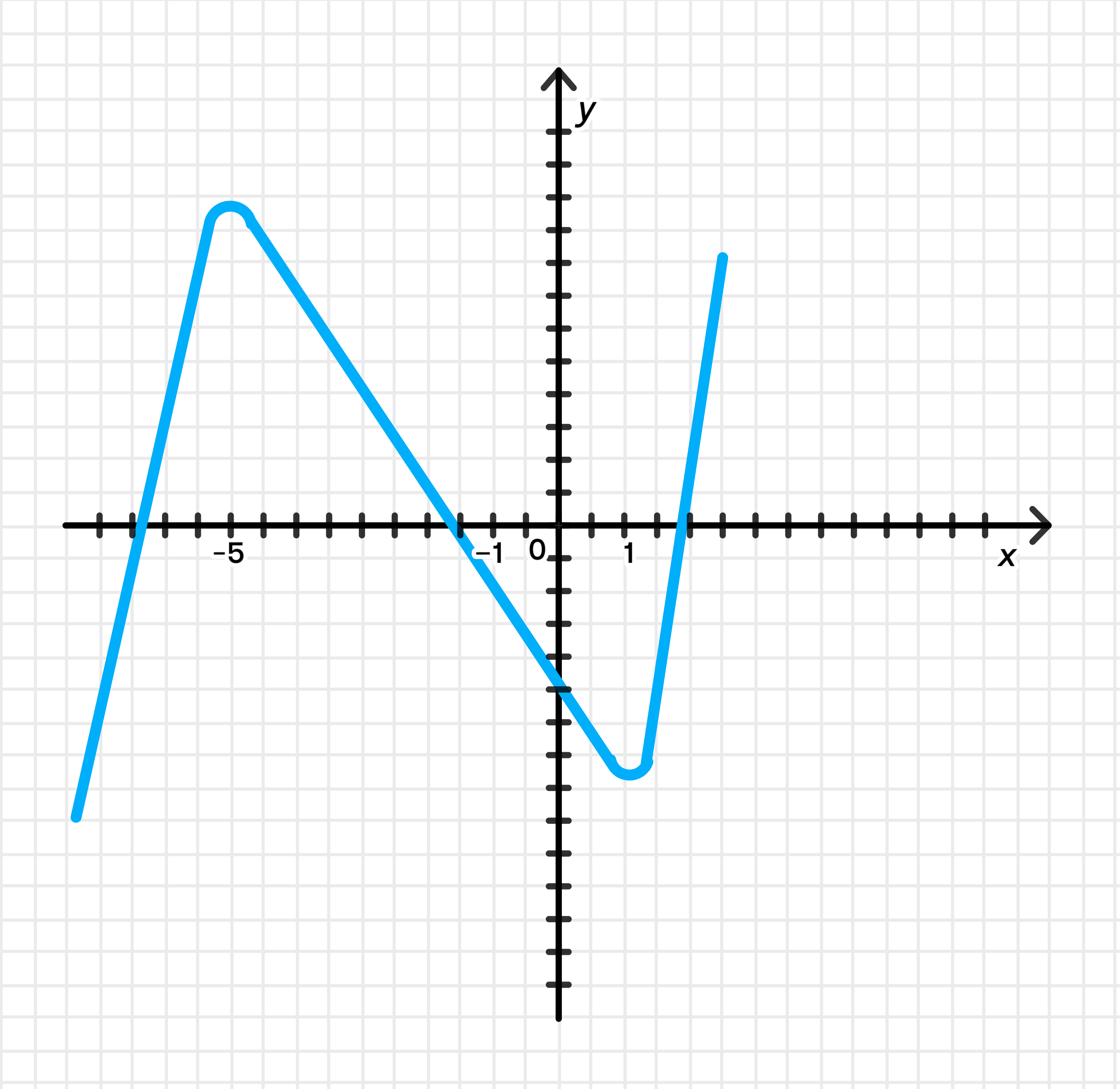
Схематичный рисунок:

Ответ: возрастает на $(-\infty; -5] \cup [1; +\infty)$ и убывает на $[-5; 1]$.

г) $f(x) = -x^4 + 8x^2 — 7$;
$f'(x) = -(x^4)’ + 8(x^2)’ — (7)’ = -4x^3 + 8 \cdot 2x — 0 = 16x — 4x^3$;

Промежуток возрастания:
$16x — 4x^3 \geq 0$;
$4x — x^3 \geq 0$;
$x(4 — x^2) \geq 0$;
$x(2 + x)(2 — x) \geq 0$;
$x \leq -2$ или $2 \leq x \leq +\infty$;

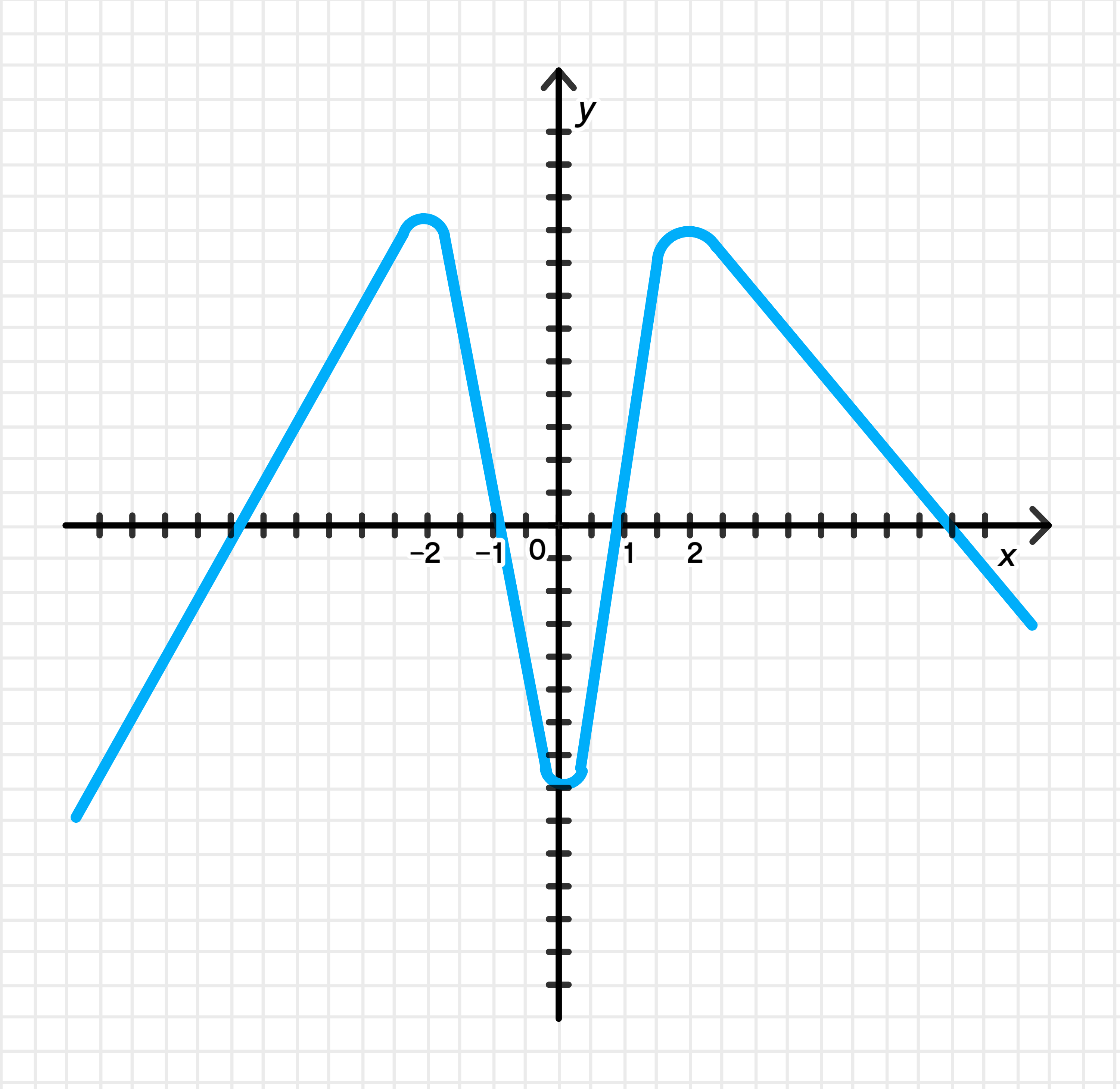
Схематичный рисунок:

Ответ: возрастает на $(-\infty; -2] \cup [0; 2]$ и убывает на $[-2; 0] \cup [2; +\infty)$.

а) $f(x) = x^3 — 3x + 2$

Шаг 1: Найдём производную

$$f'(x) = \frac{d}{dx}(x^3 — 3x + 2) = 3x^2 — 3$$

Шаг 2: Найдём критические точки

Найдем, где производная равна нулю:

$$3x^2 — 3 = 0 \Rightarrow x^2 = 1 \Rightarrow x = \pm1$$

Шаг 3: Исследуем знак производной

Рассмотрим интервалы:

• $(-\infty, -1)$: подставим $x = -2 \Rightarrow f'(-2) = 3 \cdot 4 — 3 = 9 > 0$ ⇒ возрастает
• $(-1, 1)$: подставим $x = 0 \Rightarrow f'(0) = -3 < 0$ ⇒ убывает
• $(1, +\infty)$: подставим $x = 2 \Rightarrow f'(2) = 3 \cdot 4 — 3 = 9 > 0$ ⇒ возрастает

Шаг 4: Вывод

• Возрастает: $(-\infty, -1] \cup [1, +\infty)$
• Убывает: $[-1, 1]$

Шаг 5: Схематичный график

Функция кубическая, с тремя членами, имеет S-образную форму.
Критические точки $x = -1$ и $x = 1$, это локальный максимум и минимум.
Свойства:

• $f(-1) = (-1)^3 — 3(-1) + 2 = -1 + 3 + 2 = 4$
• $f(1) = (1)^3 — 3(1) + 2 = 1 — 3 + 2 = 0$

График: $x = 1$

б) $f(x) = x^4 — 2x^2 + 1$

Шаг 1: Производная

$$f'(x) = \frac{d}{dx}(x^4 — 2x^2 + 1) = 4x^3 — 4x$$

Шаг 2: Критические точки

$$f'(x) = 4x(x^2 — 1) = 4x(x — 1)(x + 1) = 0 \Rightarrow x = -1, 0, 1$$

Шаг 3: Знаки производной на интервалах

Разобьём числовую ось по критическим точкам:

• $(-\infty, -1)$: $x = -2 \Rightarrow f'(-2) = -32 < 0$
• $(-1, 0)$: $x = -0.5 \Rightarrow f'(-0.5) > 0$
• $(0, 1)$: $x = 0.5 \Rightarrow f'(0.5) < 0$
• $(1, +\infty)$: $x = 2 \Rightarrow f'(2) = 32 > 0$

Шаг 4: Вывод

• Возрастает: $[-1, 0] \cup [1, +\infty)$
• Убывает: $(-\infty, -1] \cup [0, 1]$

Шаг 5: График

Это четная функция (график симметричен относительно оси $y$).
Значения в точках:

• $f(-1) = 1 — 2 + 1 = 0$
• $f(0) = 0 — 0 + 1 = 1$
• $f(1) = 1 — 2 + 1 = 0$

График:

в) $f(x) = x^3 + 6x^2 — 15x + 8$

Шаг 1: Производная

$$f'(x) = 3x^2 + 12x — 15$$

Шаг 2: Критические точки

$$3x^2 + 12x — 15 = 0 \Rightarrow x^2 + 4x — 5 = 0$$ $$D = 16 + 20 = 36, \quad x_{1,2} = \frac{-4 \pm \sqrt{36}}{2} = \frac{-4 \pm 6}{2} \Rightarrow x = -5, 1$$

Шаг 3: Знаки производной

• $(-\infty, -5)$: $x = -6 \Rightarrow f'(-6) = 3 \cdot 36 — 72 — 15 = 108 — 87 = 21 > 0$
• $(-5, 1)$: $x = 0 \Rightarrow f'(0) = -15 < 0$
• $(1, +\infty)$: $x = 2 \Rightarrow f'(2) = 3 \cdot 4 + 24 — 15 = 12 + 9 = 21 > 0$

Шаг 4: Вывод

• Возрастает: $(-\infty, -5] \cup [1, +\infty)$
• Убывает: $[-5, 1]$

Шаг 5: График

Функция кубическая, с двумя экстремумами:

• $f(-5) = (-125) + 6 \cdot 25 + 75 + 8 = -125 + 150 + 75 + 8 = 108$
• $f(1) = 1 + 6 — 15 + 8 = 0$

Поведение: возрастает до $x = -5$, убывает до $x = 1$, потом снова вверх.

График:

г) $f(x) = -x^4 + 8x^2 — 7$

Шаг 1: Производная

$$f'(x) = -4x^3 + 16x = 4x(-x^2 + 4) = 4x(2 + x)(2 — x)$$

Шаг 2: Критические точки

$$4x(2 — x)(2 + x) = 0 \Rightarrow x = -2, 0, 2$$

Шаг 3: Знаки производной

• $(-\infty, -2)$: $x = -3 \Rightarrow f'(-3) = 4(-3)(-9 + 4) = -60 < 0$
• $(-2, 0)$: $x = -1 \Rightarrow f'(-1) = 4(-1)(1 + 2)(2 — 1) = 4(-1)(3)(1) = -12 < 0$
• $(0, 2)$: $x = 1 \Rightarrow f'(1) = 4(1)(2 + 1)(2 — 1) = 4 \cdot 3 = 12 > 0$
• $(2, \infty)$: $x = 3 \Rightarrow f'(3) = 4(3)(-5) = -60 < 0$

Шаг 4: Вывод

• Возрастает: $(-\mathrm{\infty };-2]\cup$$[0, 2]$
• Убывает: $(-\infty, 0] \cup [2, +\infty)$

Шаг 5: График

Это чётная функция (симметрия по оси $y$).
Критические точки:

• $f(-2) = -16 + 32 — 7 = 9$
• $f(0) = -0 + 0 — 7 = -7$
• $f(2) = -16 + 32 — 7 = 9$

Имеет форму «∩» с двумя симметричными максимумами в $x = \pm2$, минимум в 0.

График: