ГДЗ по Алгебре 10 Класс Номер 44.30 Профильный Уровень Мордкович — Подробные Ответы

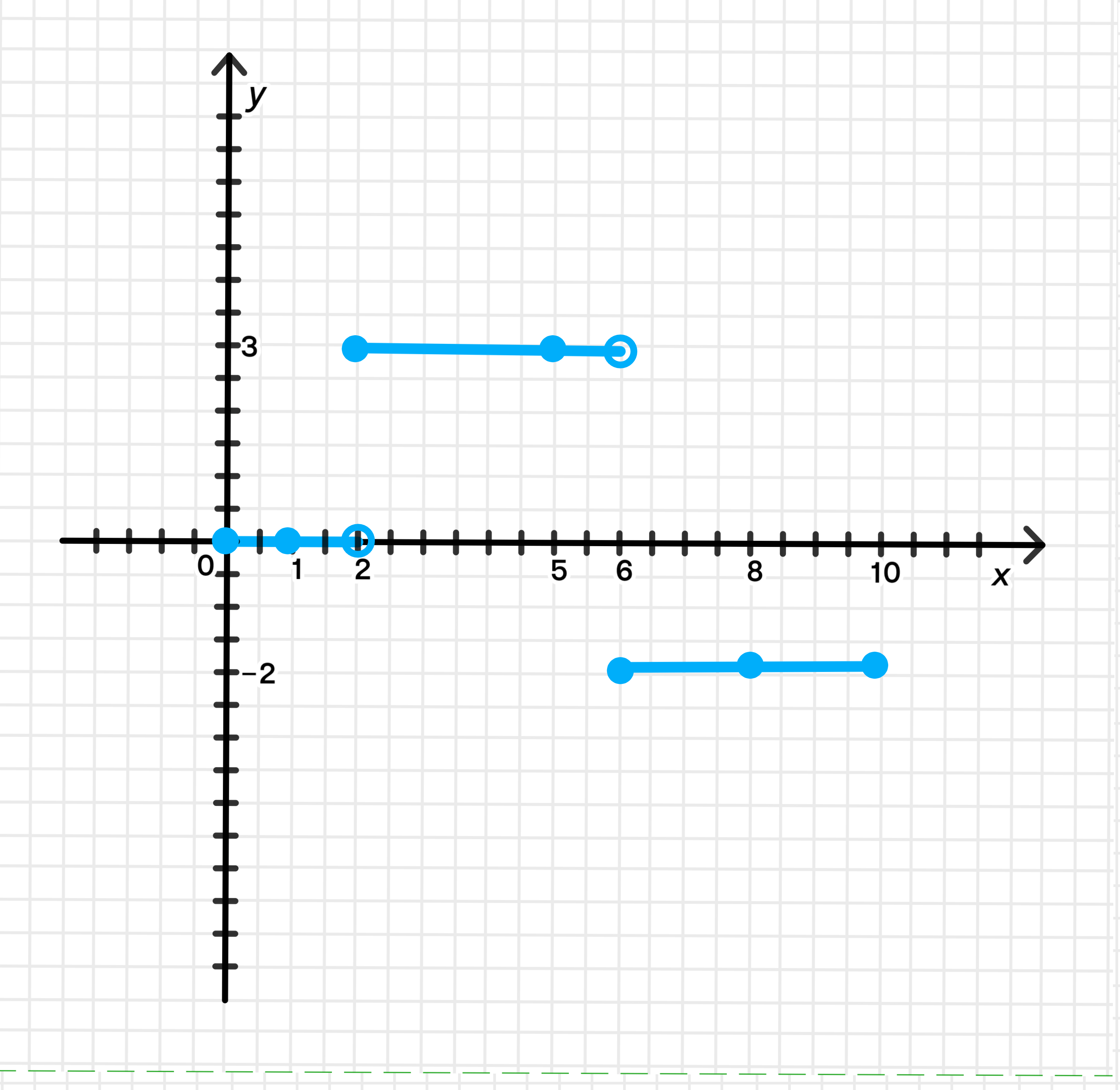
Постройте график функции $y = f(x)$, $x \in [0; 10]$, производная которой равна нулю на интервалах $(0; 2)$; $(2; 6)$; $(6; 10)$, если известно, что $f(1) = 0$, $f(5) = 3$, $f(8) = -2$.

Если производная функции равна нулю, то функция постоянна на данном промежутке, следовательно:

• $y = f(1) = 0$, если $x \in (0; 2)$;
• $y = f(5) = 3$, если $x \in (2; 6)$;
• $y = f(8) = -2$, если $x \in (6; 10)$;

График функции:

Постройте график функции $y = f(x)$, $x \in [0; 10]$,
производная которой равна нулю на интервалах $(0; 2)$; $(2; 6)$; $(6; 10)$,
если известно, что
$f(1) = 0$,
$f(5) = 3$,
$f(8) = -2$.

Шаг 1. Понимание условия

Просят построить график функции, у которой производная равна нулю на трёх интервалах:

• $(0; 2)$
• $(2; 6)$
• $(6; 10)$

Что значит, что производная функции равна нулю?
Если $f'(x) = 0$ на каком-то интервале, это означает, что функция постоянна на этом интервале.
То есть график функции на этом интервале — горизонтальная прямая (параллельная оси $x$).

Шаг 2. Выяснение значений функции на каждом интервале

Из условия нам даны значения функции в трёх точках:

• $f(1) = 0$
• $f(5) = 3$
• $f(8) = -2$

Теперь используем это, чтобы определить значения функции на каждом из трёх интервалов:

Интервал $(0; 2)$:

• На этом интервале $f'(x) = 0$, значит, $f(x)$ — постоянная.
• В этом интервале находится точка $x = 1$, а $f(1) = 0$
  Следовательно, на всём интервале $(0; 2)$:
  $f(x) = 0$

Интервал $(2; 6)$:

• Здесь также $f'(x) = 0$, значит, $f(x)$ — постоянная.
• В этом интервале находится точка $x = 5$, а $f(5) = 3$
  Следовательно, на всём интервале $(2; 6)$:
  $f(x) = 3$

Интервал $(6; 10)$:

• Здесь $f'(x) = 0$, значит, $f(x)$ — постоянная.
• В этом интервале находится точка $x = 8$, а $f(8) = -2$
  Следовательно, на всём интервале $(6; 10)$:
  $f(x) = -2$

Шаг 3. Поведение функции на концах отрезков

Интервалы, где функция постоянна, заданы как открытые, то есть:

• $f(x) = 0$ только при $x \in (0; 2)$, не включая $x = 0$ и $x = 2$
• $f(x) = 3$ при $x \in (2; 6)$, не включая $x = 2$ и $x = 6$
• $f(x) = -2$ при $x \in (6; 10)$, не включая $x = 6$ и $x = 10$

А что в точках $x = 2$ и $x = 6$?

Не указано явно, что происходит на этих границах, значит — мы не обязаны соединять отрезки непрерывно.

Возможна разрывная функция (скачки на $x = 2$, $x = 6$).

Шаг 4. Построение графика

Теперь, когда всё определено, строим график по частям:

Участок 1: $x \in (0; 2)$

• Функция постоянна, $f(x) = 0$
• График: горизонтальный отрезок на уровне $y = 0$ от $x = 0$ до $x = 2$, не включая концы.

Участок 2: $x \in (2; 6)$

• Функция постоянна, $f(x) = 3$
• График: горизонтальный отрезок на уровне $y = 3$ от $x = 2$ до $x = 6$, не включая концы.

Участок 3: $x \in (6; 10)$

• Функция постоянна, $f(x) = -2$
• График: горизонтальный отрезок на уровне $y = -2$ от $x = 6$ до $x = 10$, не включая концы.

Шаг 5. Отметим ключевые точки

Обязательно обозначим три известные точки на графике:

• $(1, 0)$ — точка на первом участке
• $(5, 3)$ — точка на втором участке
• $(8, -2)$ — точка на третьем участке

Эти точки лежат на соответствующих отрезках, где функция постоянна.

Шаг 6. Вывод

Функция $f(x)$ имеет следующий вид:

• $f(x) = 0$, при $x \in (0; 2)$
• $f(x) = 3$, при $x \in (2; 6)$
• $f(x) = -2$, при $x \in (6; 10)$

Функция разрывна в точках $x = 2$ и $x = 6$.
Внутри каждого интервала — это горизонтальная прямая, соответствующая постоянному значению функции.

График: