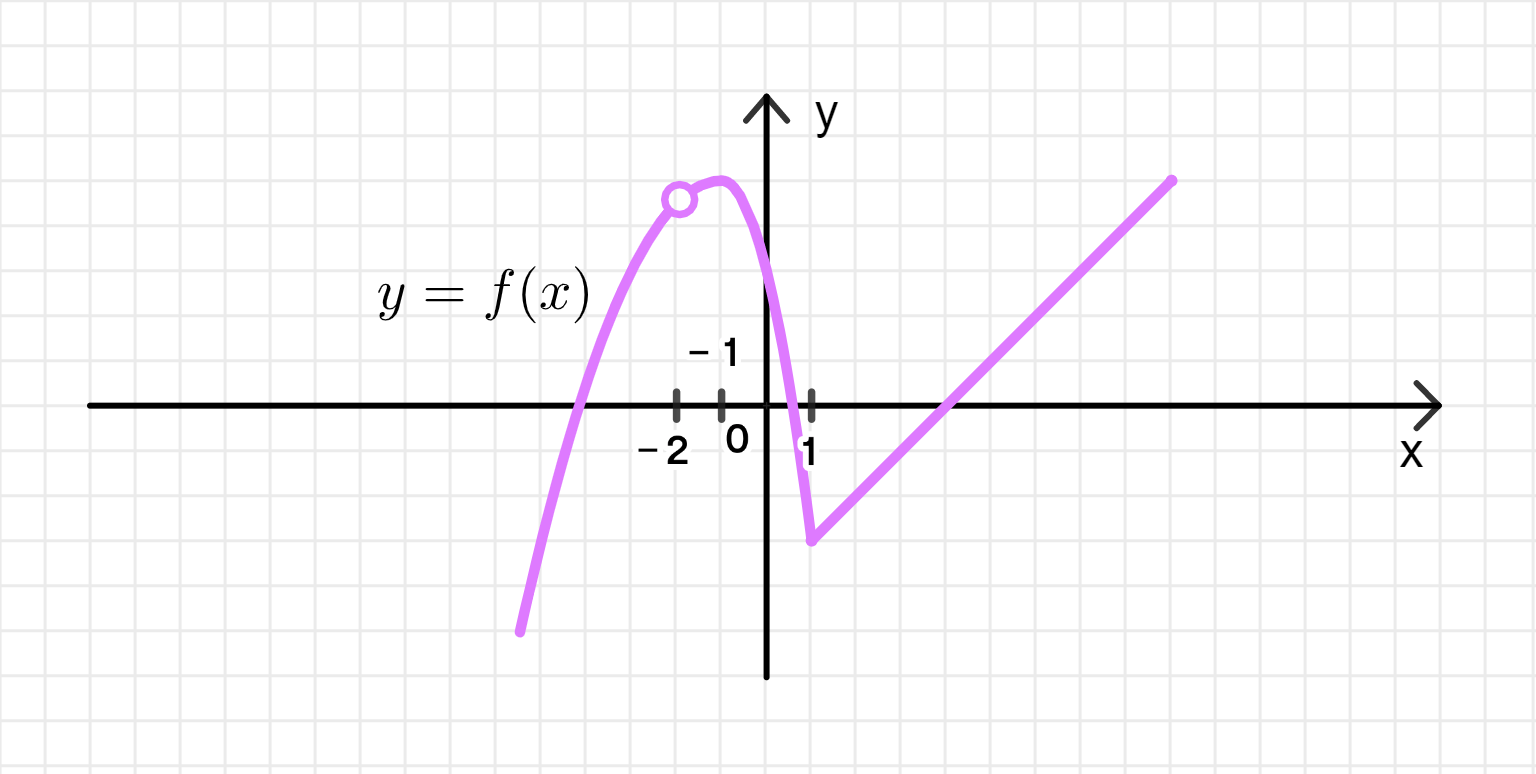Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 44.43 Профильный Уровень Мордкович — Подробные Ответы
Постройте эскиз графика какой-нибудь функции, обладающей указанными свойствами:
а) Функция имеет две точки максимума, одну точку минимума и является ограниченной;
б) Функция возрастает при и при и убывает на промежутке , точка является критической, а точка — стационарной;
в) Функция имеет разрыв в точке , максимум в точке и минимум в точке ;
г) Функция имеет горизонтальную асимптоту при , одну точку максимума и одну точку минимума.
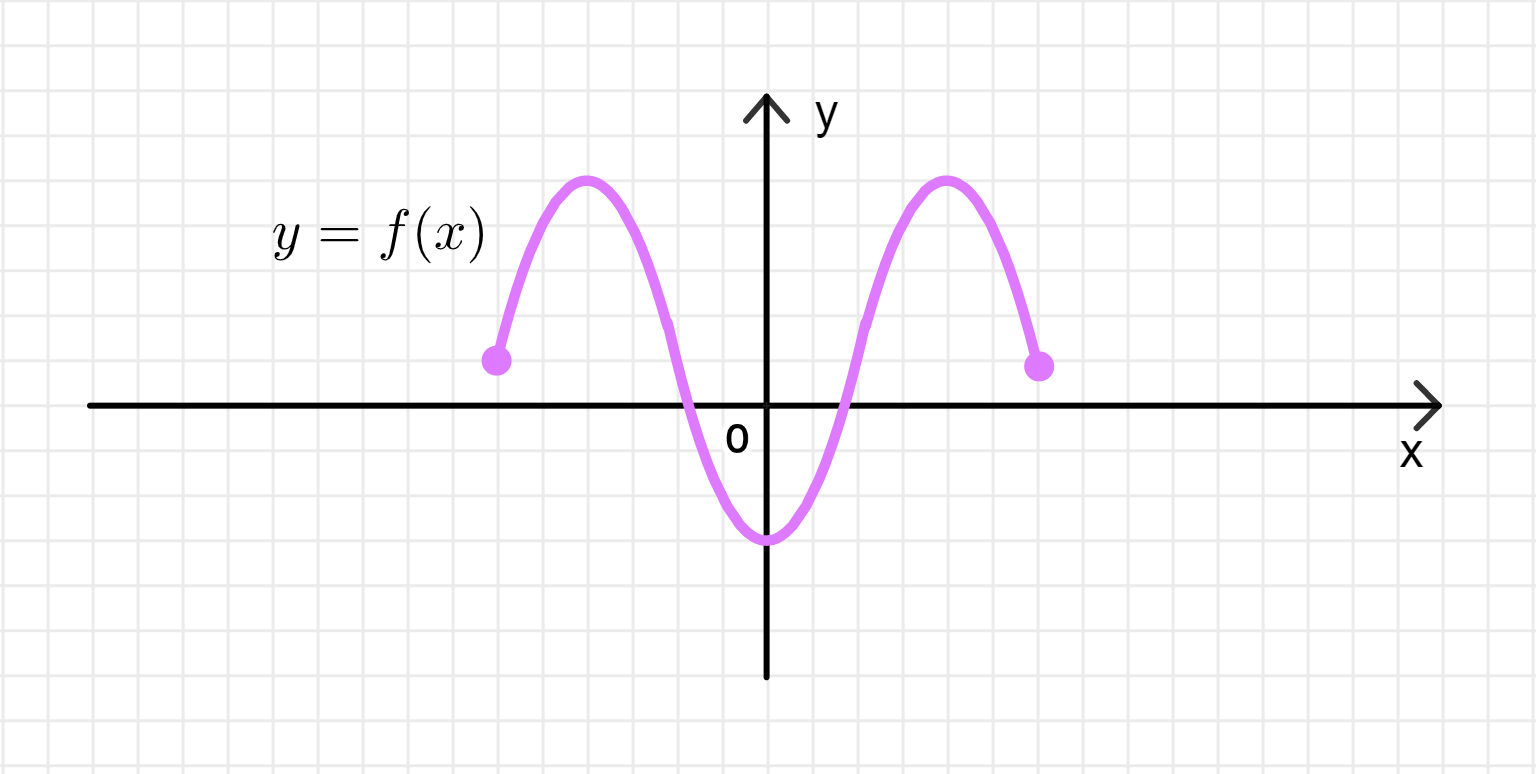
а) Функция имеет две точки максимума, одну точку минимума и является ограниченной:
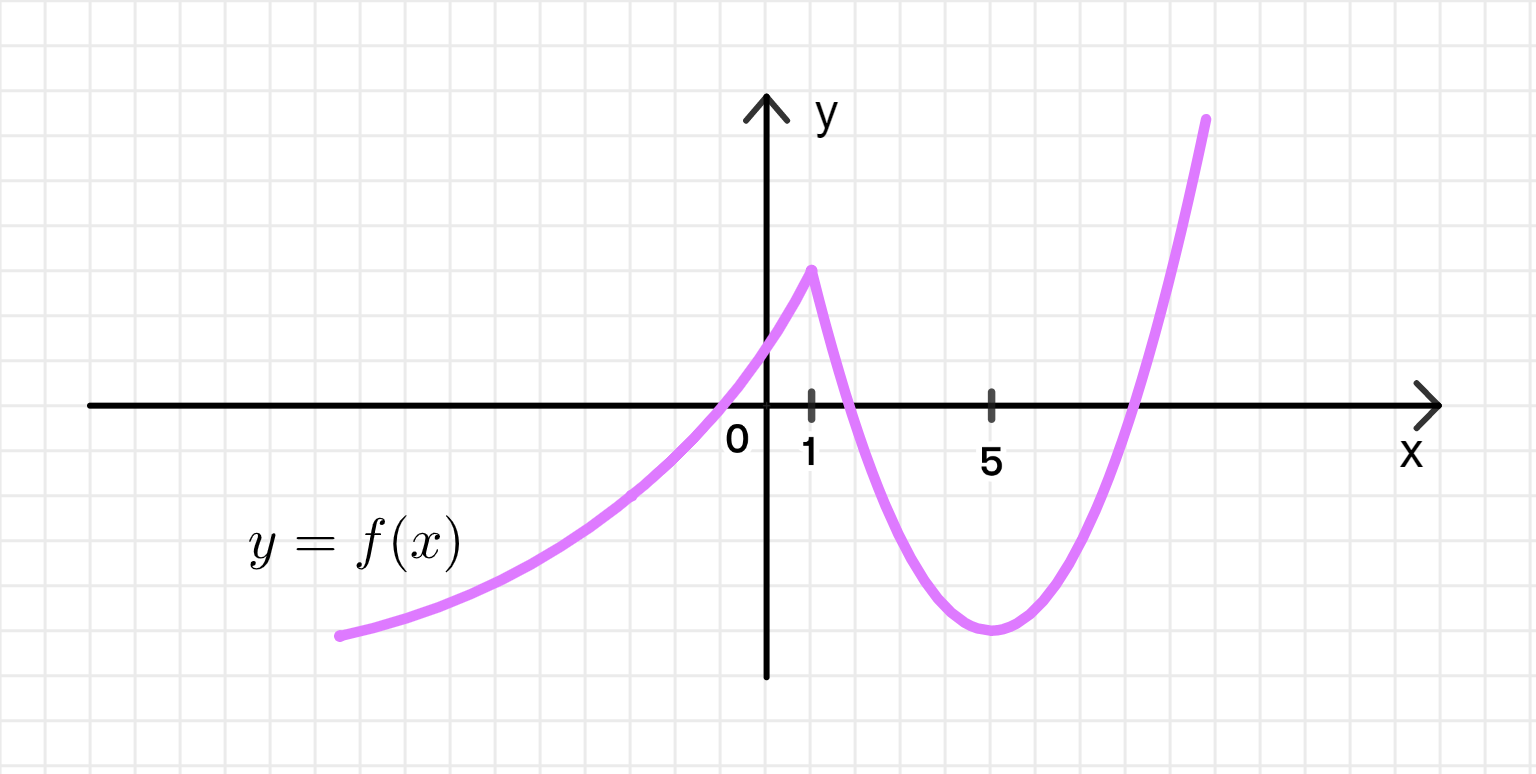
б) Функция возрастает при и при и убывает на промежутке , точка является критической, а точка — стационарной:
в) Функция имеет разрыв в точке , максимум в точке и минимум в точке :
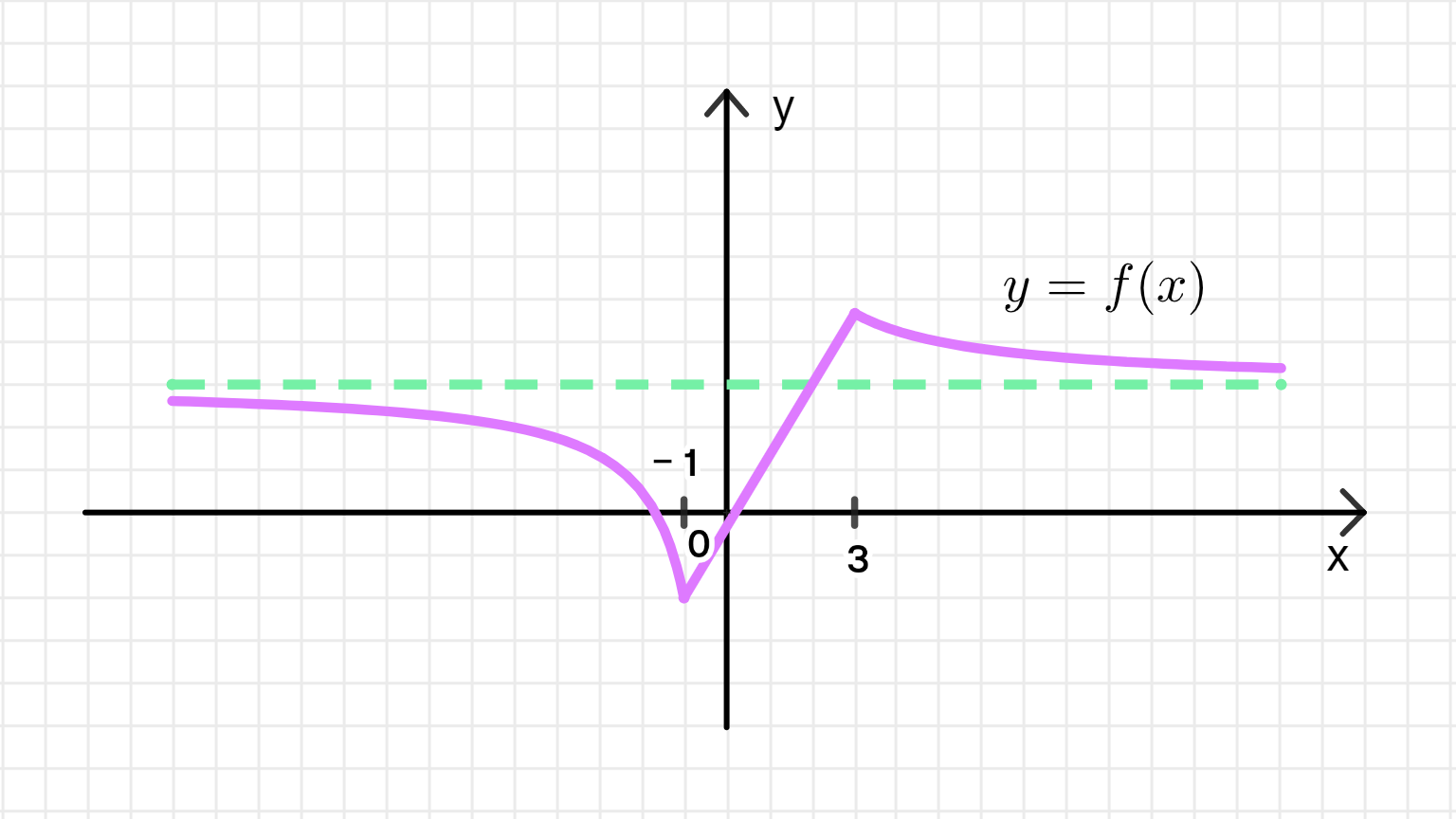
г) Функция имеет горизонтальную асимптоту при , одну точку максимума и одну точку минимума:
а) Функция имеет две точки максимума, одну точку минимума и является ограниченной:
График функции:
- Данная функция имеет два максимума, что означает, что существует две точки, в которых функция принимает наибольшие значения в окрестностях этих точек.
- Одно минимальное значение у функции, которое также находится в одной из точек (или в интервале между максимумами).
- Функция ограничена, то есть существует такая верхняя и нижняя граница, между которыми функция изменяется. Это важно для понимания того, что график функции никогда не выходит за пределы этих границ.
Алгоритм построения графика:
- Выберите две точки, которые будут являться максимумами (например, и ), и одну точку минимума (например, ).
- Убедитесь, что на всем промежутке между точками максимумов функция не выходит за пределы между этими максимальными и минимальными значениями.
- График должен быть ограничен вертикальными и горизонтальными прямыми, обозначающими пределы значений функции.
- Важно, чтобы функция не имела асимптот, разрывов или других особенностей, выходящих за рамки ограниченности.
б) Функция возрастает при и при и убывает на промежутке , точка является критической, а точка — стационарной:
Ключевые моменты:
- Функция возрастает при и при . Это значит, что её производная на этих интервалах положительна.
- На промежутке функция убывает, следовательно, её производная отрицательна на этом промежутке.
- Точка является критической. Это означает, что в этой точке производная функции равна нулю, и возможно существует экстремум (максимум или минимум) или точка перегиба.
- Точка — стационарная. Это также означает, что производная функции равна нулю в этой точке, но на этом промежутке функция уже убывает.
Алгоритм построения графика:
- Начнем с построения двух интервалов: до точки и после точки , где функция возрастает.
- Далее, на промежутке между и , нарисуем убывающую часть функции.
- Убедитесь, что на точке функция имеет критическую точку (то есть касательная к графику будет горизонтальной).
- На точке функция должна быть стационарной, то есть график также будет иметь горизонтальную касательную, но дальше функция не будет изменяться на этом интервале.
в) Функция имеет разрыв в точке , максимум в точке и минимум в точке :
Ключевые моменты:
- Разрыв функции в точке означает, что график функции в этой точке либо не определен, либо имеет скачок (например, переход от положительного значения к отрицательному или наоборот).
- Функция имеет максимум в точке , что означает, что значение функции в этой точке больше, чем на некой окрестности вокруг этой точки.
- Минимум функции находится в точке , что аналогично максиму, но наоборот — значение функции в этой точке меньше, чем в окрестности этой точки.
Алгоритм построения графика:
- Начнем с разрыва функции в точке . Для этого нужно провести вертикальную линию в этой точке, чтобы показать отсутствие значений функции в этой точке.
- После разрыва добавим максимум в точке и минимум в точке , соблюдая, что значение функции в точке выше, чем в ближайших точках, а в точке ниже, чем в соседних точках.
- Построив такие участки графика, удостоверьтесь, что между максимумом и минимумом функция не имеет разрывов и изменений направления.
г) Функция имеет горизонтальную асимптоту при , одну точку максимума и одну точку минимума:
Ключевые моменты:
- Горизонтальная асимптота означает, что по мере того, как стремится к бесконечности, значение функции приближается к 3.
- Функция имеет одну точку максимума и одну точку минимума. Это значит, что между двумя экстремумами функция будет изменять направление своего роста и спада.
Алгоритм построения графика:
- Начнем с горизонтальной асимптоты , что будет означать, что при график будет приближаться к прямой .
- Далее, добавим максимум в определенной точке, например, при , и минимум в точке .
- Убедимся, что функция сначала возрастает, достигая максимума, затем убывает до минимума и снова возрастает, стремясь к асимптоте.