ГДЗ по Алгебре 10 Класс Номер 44.44 Профильный Уровень Мордкович — Подробные Ответы

а) Постройте эскиз графика функции, дифференцируемой на интервале $(a, b)$, имеющей на этом интервале одну точку минимума, две точки максимума и не имеющей наименьшего значения.

б) Постройте эскиз графика функции, дифференцируемой на интервале $(a, b)$, имеющей на нём две точки минимума, две точки максимума, но не имеющей ни наименьшего, ни наибольшего значений.

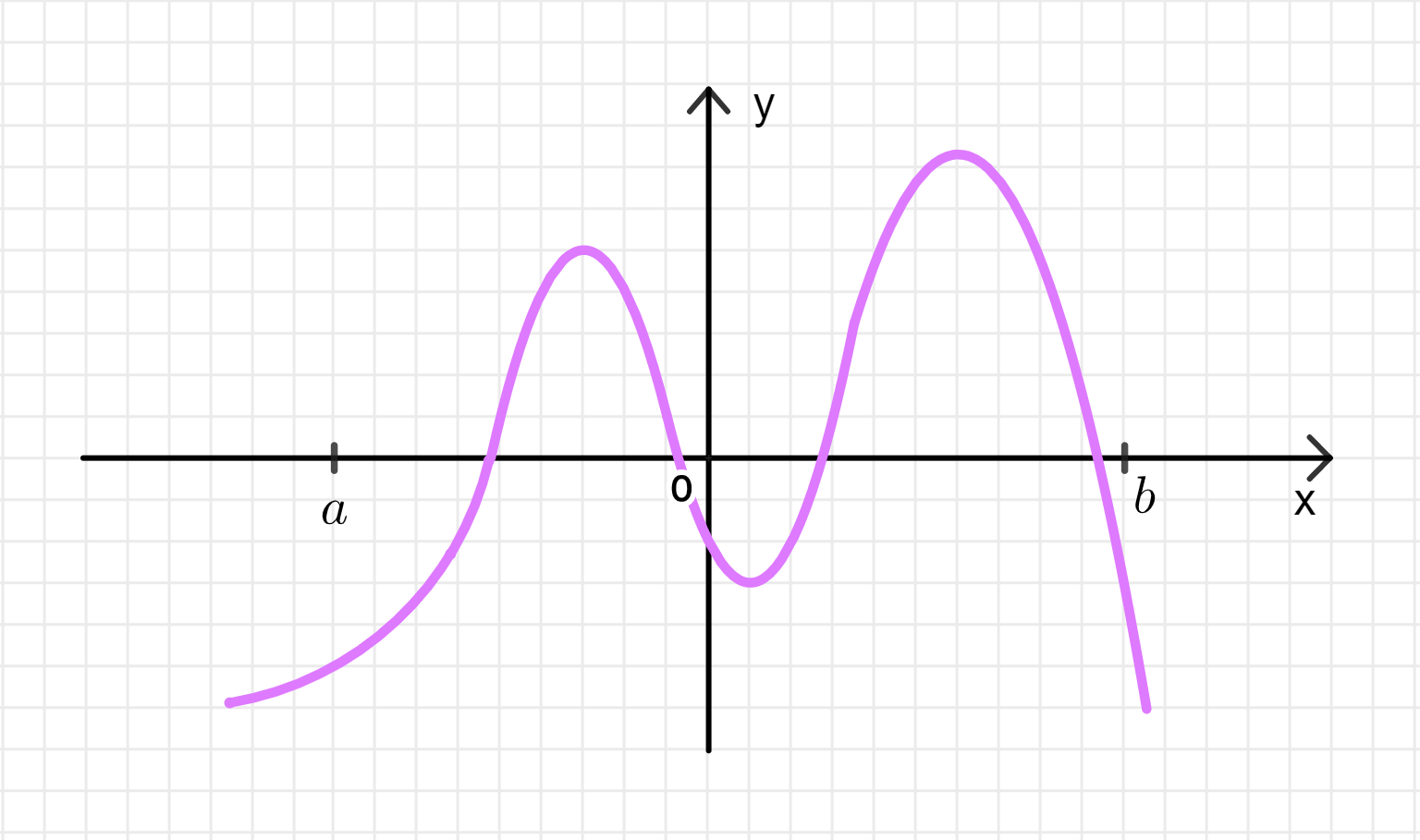
а) Эскиз графика функции, дифференцируемой на интервале $(a; b)$, имеющей на этом интервале одну точку минимума, две точки максимума и не имеющей наименьшего значения:

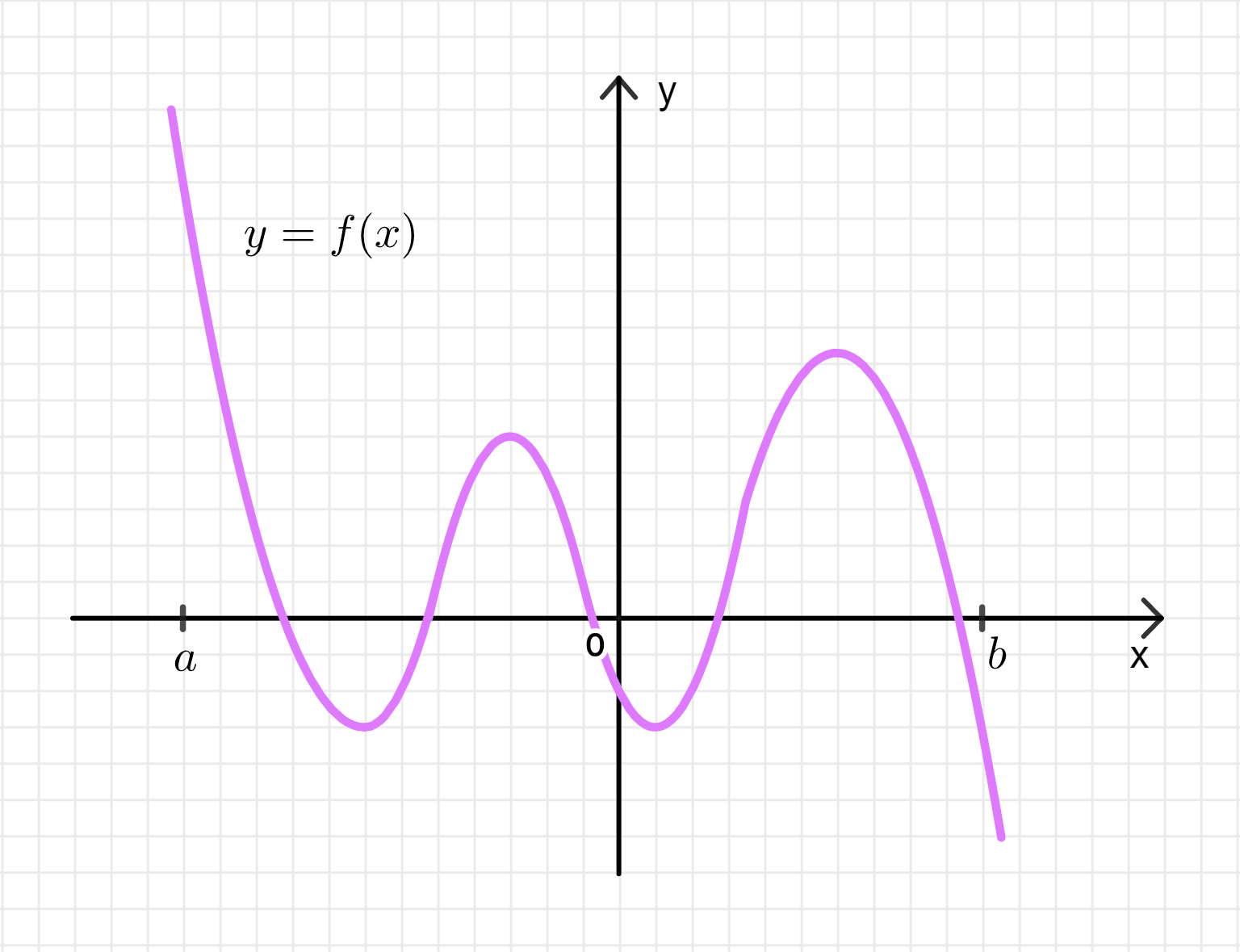
б) Эскиз графика функции, дифференцируемой на интервале $(a, b)$, имеющей на нем две точки минимума, две точки максимума, но не имеющей ни наибольшего, ни наименьшего значений:

Часть а)

Задача: Построить эскиз графика функции, дифференцируемой на интервале $(a, b)$, имеющей на этом интервале одну точку минимума, две точки максимума и не имеющей наименьшего значения.

Шаг 1: Описание функции и её особенностей

Нам дана функция, которая дифференцируема на интервале $(a, b)$, что означает, что её производная существует на всём интервале. Заданные особенности:

• Одна точка минимума — функция имеет только одно локальное минимум на интервале $(a, b)$. Это значит, что в этой точке производная функции равна нулю (так как производная функции в точке минимума равна нулю), и функция меняет свой знак (переходит с убывающей на возрастающую).
• Две точки максимума — функция имеет два локальных максимума. В этих точках производная также равна нулю, и функция меняет свой знак (с возрастающей на убывающую).
• Не имеет наименьшего значения — это означает, что функция не ограничена снизу на интервале $(a, b)$. В частности, она может стремиться к отрицательной бесконечности.

Шаг 2: Характеристики графика

На графике будет несколько локальных экстремумов:

• Одна точка минимума, где функция достигает локального минимального значения.
• Две точки максимума, где функция достигает локальных максимальных значений.

Из-за того, что функция не имеет наименьшего значения, она может продолжать уменьшаться на некоторых участках интервала, возможно, стремясь к минус бесконечности. Это важно, потому что на графике такие участки будут направлены вниз без ограничения снизу.

Также, поскольку функция дифференцируема на интервале, она будет гладкой и без разрывов.

Шаг 3: Построение графика

Для построения графика функции на основе этих характеристик, можно начать с того, чтобы нарисовать:

• Линию, которая имеет два пика (локальные максимумы) и одну впадину (локальный минимум).
• Линия, представляющая функцию, не должна иметь минимальной точки, которая бы ограничивала её снизу. Это может быть выполнено, например, путём продолжения графика вниз.

Часть б)

Задача: Построить эскиз графика функции, дифференцируемой на интервале $(a, b)$, имеющей на нем две точки минимума, две точки максимума, но не имеющей ни наибольшего, ни наименьшего значений.

Шаг 1: Описание функции и её особенностей

Нам дана функция, которая также дифференцируема на интервале $(a, b)$, но с другими характеристиками:

• Две точки минимума — функция имеет два локальных минимума. Эти точки аналогичны тем, что мы рассмотрели в части а), где производная функции равна нулю, и функция меняет свой знак на каждом минимуме (с возрастающей на убывающую).
• Две точки максимума — аналогично предыдущей части, функции есть два локальных максимума.
• Не имеет ни наибольшего, ни наименьшего значений — эта характеристика означает, что функция не ограничена сверху или снизу. Она может продолжать возрастать и уменьшаться по мере движения вдоль интервала. Нет ни максимума, ни минимума, к которым стремится функция.

Шаг 2: Характеристики графика

На графике будет несколько локальных экстремумов:

• Два локальных минимума, где функция достигает минимальных значений на своих участках.
• Два локальных максимума, где функция достигает максимальных значений на своих участках.

Функция не будет иметь глобального минимума или максимума. Это можно представить как волнообразную линию, которая будет продолжать расти и убывать на протяжении всего интервала.

Функция будет колебаться, но ни в какой точке она не будет ограничена сверху или снизу. Это предполагает, что график функции может продолжать расти и уменьшаться на протяжении всего интервала.

Шаг 3: Построение графика

График функции для этого случая будет выглядеть как периодическая волна, где:

• Функция будет иметь два пика (максимумы) и два минимальных значения (минимумы).
• Между этими точками график будет продолжать колебаться, при этом функции не будет наибольшего или наименьшего значения, она будет стремиться к бесконечности в обе стороны.