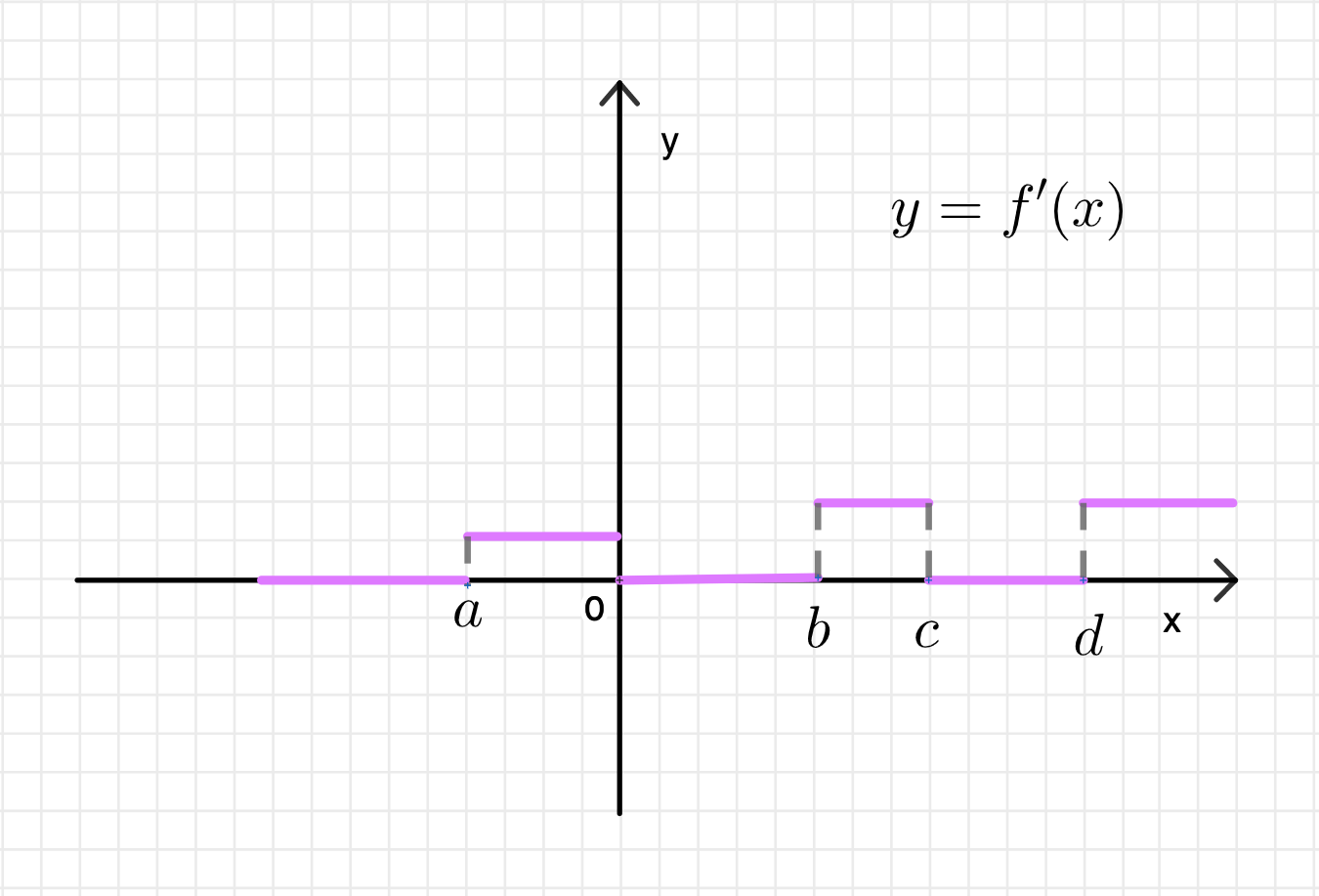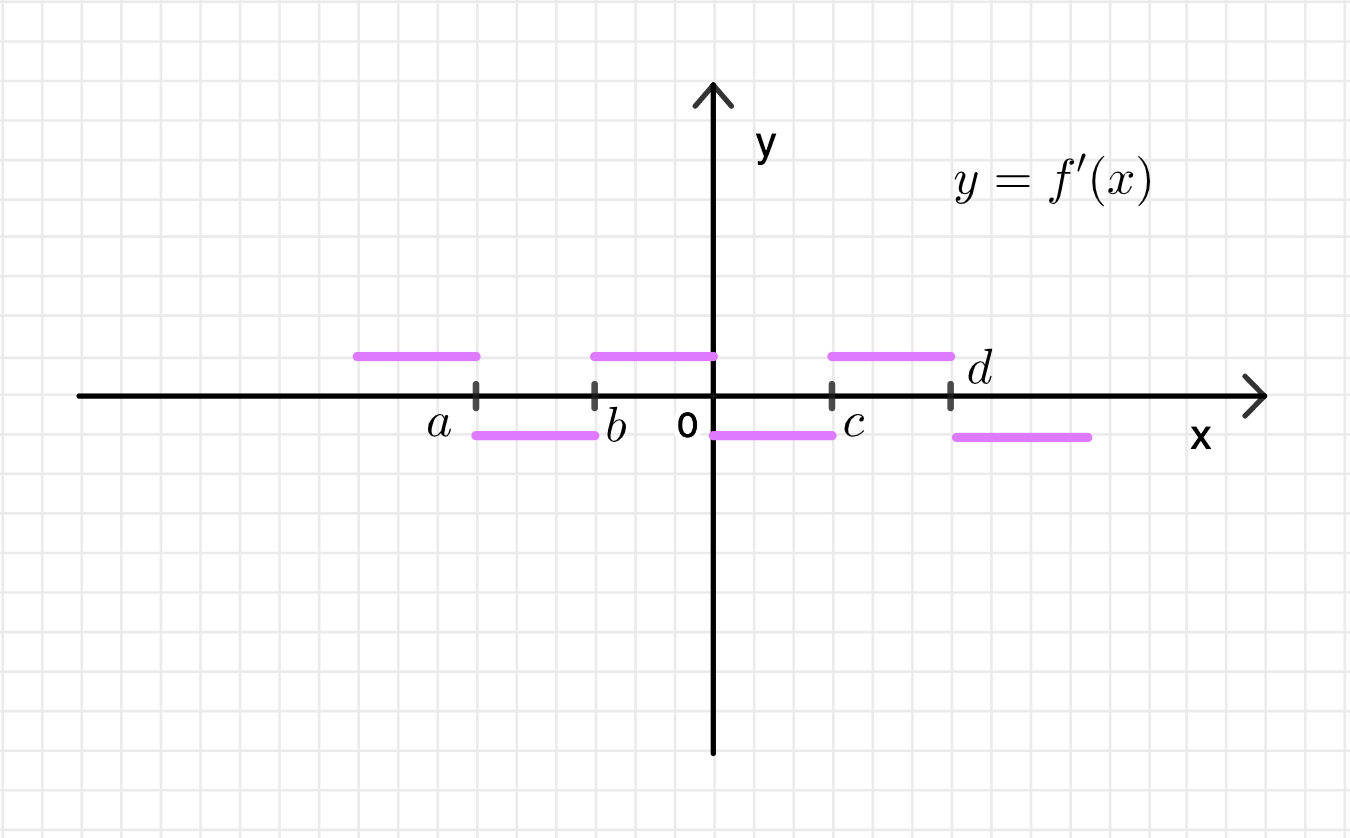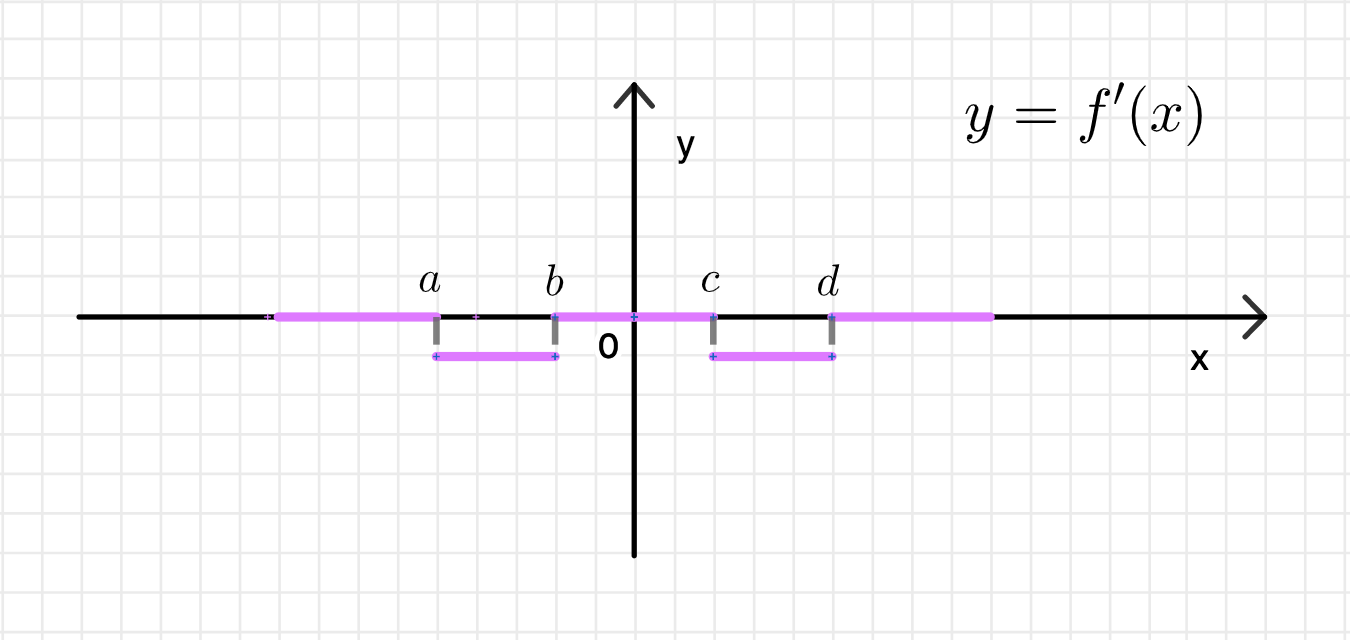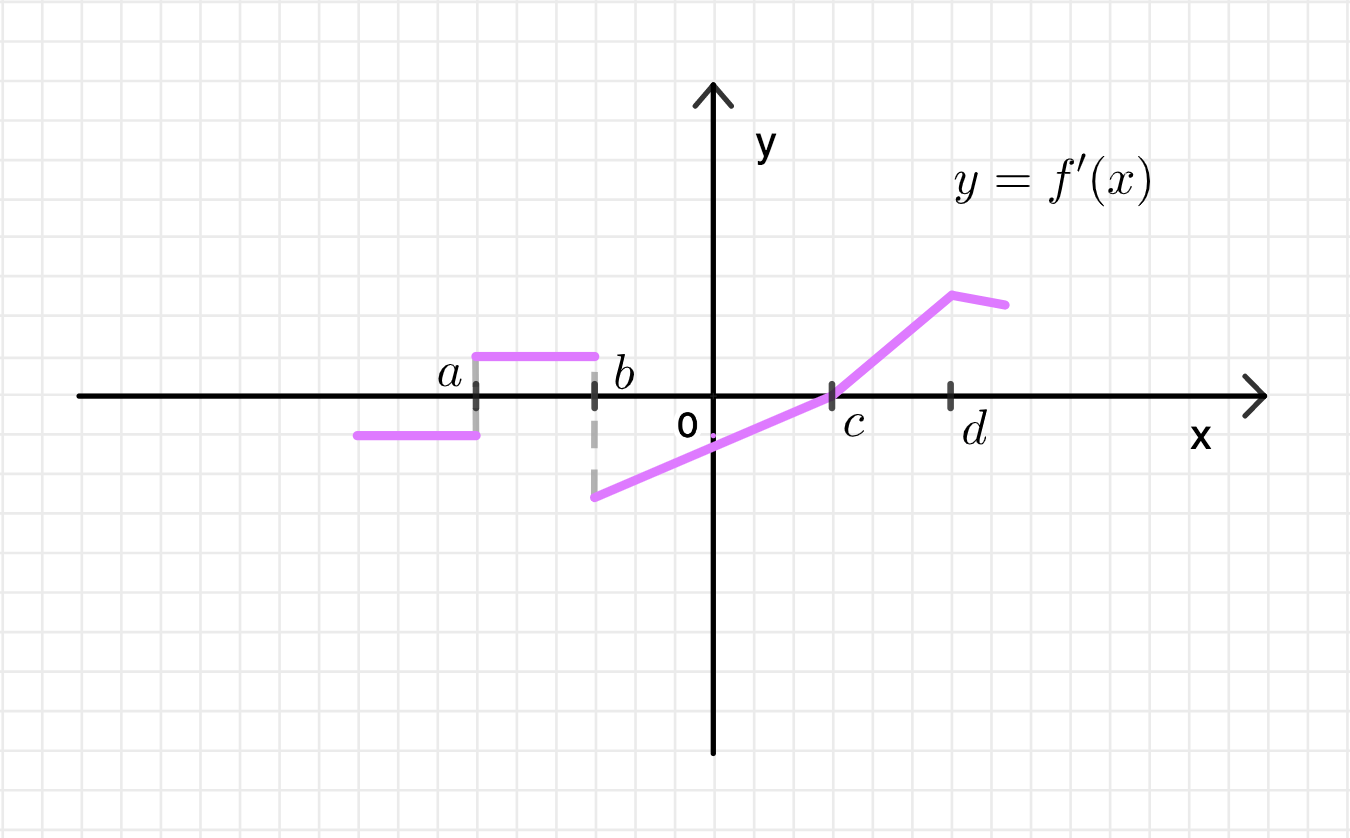ГДЗ по Алгебре 10 Класс Номер 44.47 Профильный Уровень Мордкович — Подробные Ответы

Постройте эскиз графика функции $y = f(x)$, $x \in \mathbb{R}$, по графику производной, изображённому на заданном рисунке:

а) рис. 125;
б) рис. 126;
в) рис. 127;
г) рис. 128.

а) Рисунок 125:

б) Рисунок 126:

в) Рисунок 127:

г) Рисунок 128:

Основные принципы:

1. Когда производная положительна $f'(x) > 0$, функция $f(x)$ возрастает.
2. Когда производная отрицательна $f'(x) < 0$, функция $f(x)$ убывает.
3. Когда производная равна нулю $f'(x) = 0$, функция $f(x)$ может иметь экстремум (максимум или минимум), или быть горизонтальной.
4. Наклон функции в каждой точке определяется значением её производной в этой точке.
5. Для построения графика функции нам нужно учитывать изменения наклона на каждом интервале.

а) Рисунок 125 (График производной):

• График производной на этом рисунке является ступенчатой функцией:
  • От $a$ до $b$: Производная положительна, это означает, что функция $f(x)$ возрастает.
  • От $b$ до $c$: Производная равна нулю, то есть функция $f(x)$ на этом участке постоянна.
  • От $c$ до $d$: Производная снова положительна, функция $f(x)$ снова возрастает.

Как строить график функции:

• Начинаем с произвольной точки, например $f(0) = 0$.
• На интервале $a$ до $b$ функция будет возрастать. Нарисуем её как возрастающую прямую.
• На интервале $b$ до $c$ функция будет постоянной (горизонтальная линия).
• На интервале $c$ до $d$ функция снова будет возрастать, рисуем её как возрастающую прямую.

б) Рисунок 126 (График производной):

• График производной имеет пилообразную форму:
  • От $a$ до $b$: Производная положительна, функция $f(x)$ возрастает.
  • От $b$ до $c$: Производная отрицательна, функция $f(x)$ убывает.
  • От $c$ до $d$: Производная снова положительна, функция $f(x)$ снова возрастает.

Как строить график функции:

• Начинаем с произвольной точки $f(0) = 0$.
• На интервале $a$ до $b$ функция будет возрастать. Нарисуем её как возрастающую прямую.
• На интервале $b$ до $c$ функция будет убывать, рисуем убывающую прямую.
• На интервале $c$ до $d$ функция снова возрастает. Нарисуем возрастающую прямую.
• Важно: на каждом переходе от одного интервала к другому учесть точку, где производная меняет знак.

в) Рисунок 127 (График производной):

• Производная на этом графике постоянно отрицательна:
  • От $a$ до $b$: Производная отрицательна, функция $f(x)$ убывает.
  • От $b$ до $c$: Производная остаётся отрицательной, функция $f(x)$ продолжает убывать.
  • От $c$ до $d$: Производная остаётся отрицательной, функция $f(x)$ продолжает убывать.

Как строить график функции:

• Начинаем с произвольной точки, например $f(0) = 0$.
• На интервале $a$ до $d$ функция будет монотонно убывать. Рисуем убывающую кривую, исходя из поведения производной.

г) Рисунок 128 (График производной):

• График производной представляет собой плавную кривую, которая сначала положительна, затем становится отрицательной, а затем снова положительной:
  • От $a$ до $b$: Производная положительна, функция $f(x)$ возрастает.
  • От $b$ до $c$: Производная отрицательна, функция $f(x)$ убывает.
  • От $c$ до $d$: Производная снова положительна, функция $f(x)$ снова возрастает.

Как строить график функции:

• Начинаем с произвольной точки $f(0) = 0$.
• На интервале $a$ до $b$ функция будет возрастать, рисуем её возрастающей.
• На интервале $b$ до $c$ функция будет убывать, рисуем её убывающей.
• На интервале $c$ до $d$ функция снова будет возрастать, рисуем её возрастающей.

Общее руководство по построению графиков:

Исследование графика производной:

• Выясните, где производная положительна, где отрицательна, и где равна нулю.
• Это даст вам ключевые моменты для построения графика функции.

Анализ экстремумов:

• Где производная равна нулю, функция может иметь максимум или минимум. Это важно для формирования изгибов.

Построение графика:

• Начинайте с произвольной точки (например, $f(0) = 0$).
• Нарисуйте график функции, учитывая, где она возрастает или убывает, а также где она имеет экстремумы или становится постоянной.

Логика построения:

• Если производная положительна, функция будет расти.
• Если производная отрицательна, функция будет убывать.
• Если производная равна нулю, функция будет постоянной или может иметь экстремум.