Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 44.64 Профильный Уровень Мордкович — Подробные Ответы
Исследуйте функцию на монотонность и экстремумы и постройте ее график:
а) ;
б) ;
в) ;
г)
а) ;
Промежуток возрастания:
Вершины функции:
Некоторые точки:
График функции:
Ответ: возрастает на и убывает на ;
б) ;
, значит при любом значении ;
Некоторые точки:
График функции:
Ответ: возрастает на всей числовой прямой.
в) ;
Промежуток возрастания:
Вершины функции:
Некоторые точки:
График функции:
Ответ: возрастает на и убывает на ;
г) ;
Промежуток возрастания:
Вершины функции:
Некоторые точки:
График функции:
Ответ: возрастает на и убывает на ;
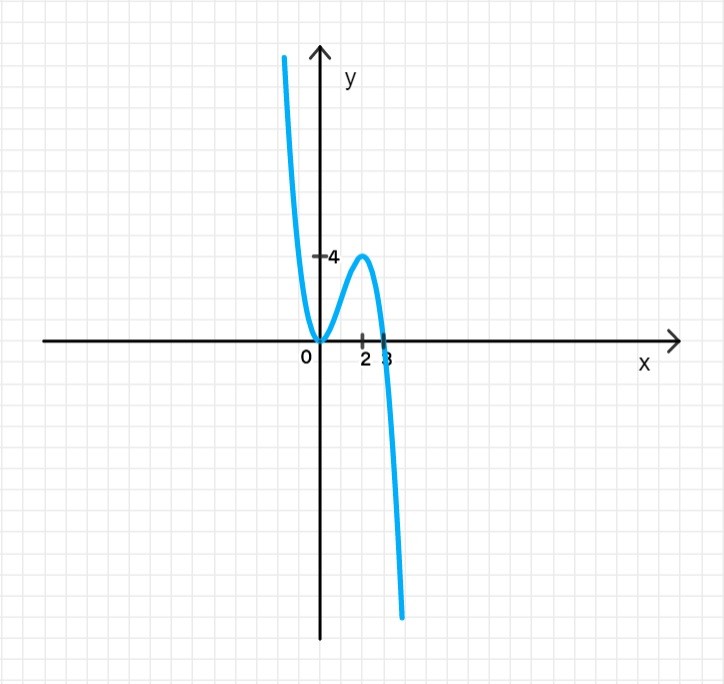
а)
1. Нахождение производной:
Для начала найдем первую производную функции . Мы применяем правила дифференцирования для каждого слагаемого по отдельности:
Дифференцируем:
Применяем стандартные правила дифференцирования:
Таким образом, производная функции равна:
2. Промежутки возрастания и убывания:
Для того чтобы найти промежутки возрастания и убывания функции, нужно исследовать знак первой производной. Для этого решим неравенство:
Выносим общий множитель :
Теперь исследуем это произведение на знак. У нас есть два множителя: и . Мы решаем неравенство поэтапно:
- при
- при
Таким образом, неравенство выполняется, когда:
Это означает, что функция возрастает на промежутке .
3. Вершины функции:
Теперь найдем значения функции на концах промежутка для определения максимума и минимума:
- В точке :
- В точке :
Таким образом, в точке , а в точке .
4. Некоторые точки функции:
Для построения графика определим значения функции для нескольких значений :
5. График функции:
Функция представляет собой кубическую функцию, и её график будет иметь форму, напоминающую два поворота: сначала убывающий, затем возрастает, а потом снова убывает. Вершины функции — это точки минимума и максимума.
Ответ:
- Функция возрастает на .
- Функция убывает на .
- Точка максимума: .
- Точка минимума: .
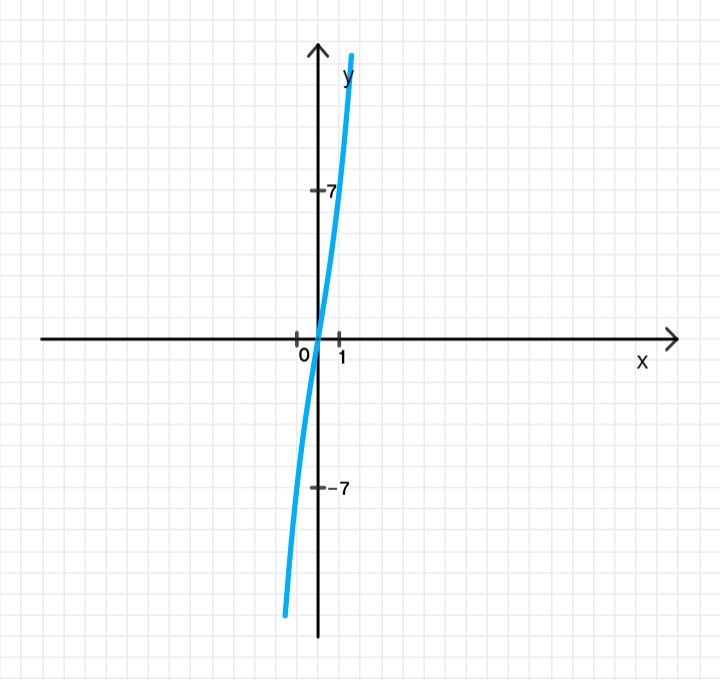
б)
1. Нахождение производной:
Найдем первую производную функции:
Дифференцируем:
Таким образом, производная функции равна:
2. Промежутки возрастания и убывания:
Производная всегда положительна, так как для всех . Следовательно, производная всегда больше нуля, то есть функция возрастает на всей числовой прямой.
Ответ:
- Функция возрастает на всей числовой прямой.
3. Некоторые точки функции:
Для построения графика определим значения функции для нескольких значений :
4. График функции:
Функция является монотонно возрастающей функцией на всей числовой прямой, так как её производная всегда положительна.
Ответ:
- Функция возрастает на всей числовой прямой.
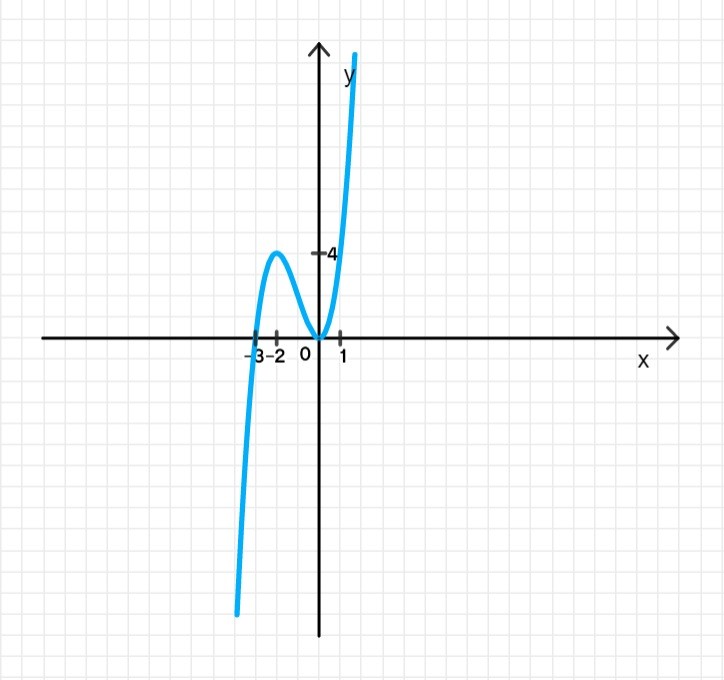
в)
1. Нахождение производной:
Найдем первую производную функции:
Дифференцируем:
Таким образом, производная функции равна:
2. Промежутки возрастания и убывания:
Для того чтобы найти промежутки возрастания и убывания функции, нужно исследовать знак первой производной. Для этого решим неравенство:
Выносим общий множитель :
Теперь решим неравенство. У нас есть два множителя: и . Исследуем знак каждого из множителей:
- при
- при
Таким образом, неравенство выполняется при:
Это означает, что функция возрастает на промежутке , а убывает на промежутке .
3. Вершины функции:
Теперь найдем значения функции на концах промежутков и в критических точках:
- В точке :
- В точке :
4. Некоторые точки функции:
Для построения графика определим значения функции для нескольких значений :
5. График функции:
Функция является кубической функцией, её график имеет две точки экстремума: одну точку максимума при и одну точку минимума при .
Ответ:
- Функция возрастает на .
- Функция убывает на .
- Точка максимума: .
- Точка минимума: .
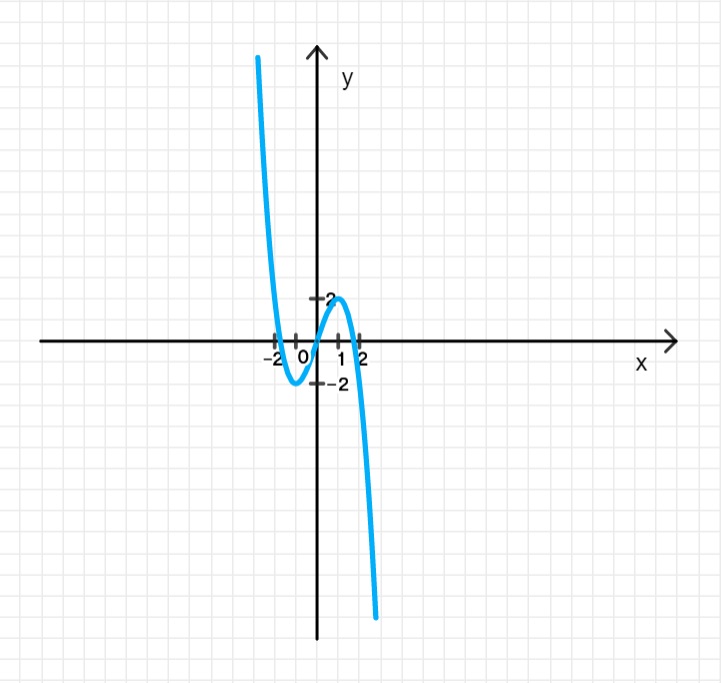
г)
1. Нахождение производной:
Найдем первую производную функции:
Дифференцируем:
Таким образом, производная функции равна:
2. Промежутки возрастания и убывания:
Для того чтобы найти промежутки возрастания и убывания функции, нужно исследовать знак первой производной. Для этого решим неравенство:
Решим неравенство:
Это означает, что функция возрастает на промежутке и убывает на промежутках .
3. Вершины функции:
Теперь найдем значения функции в точках, где производная равна нулю:
- В точке :
- В точке :
4. Некоторые точки функции:
Для построения графика определим значения функции для нескольких значений :
5. График функции:
Функция является кубической функцией с двумя точками экстремума: одна точка максимума при и одна точка минимума при .
Ответ:
- Функция возрастает на .
- Функция убывает на .
- Точка максимума: .
- Точка минимума: .