Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 44.66 Профильный Уровень Мордкович — Подробные Ответы
Исследуйте функцию на монотонность и экстремумы и постройте ее график:
а) ;
б) ;
в) ;
г)
а) ;
;
;
Промежуток возрастания:
;
;
, тогда:
;
;
;
;
или ;
Вершины функции:
;
;
Некоторые точки:
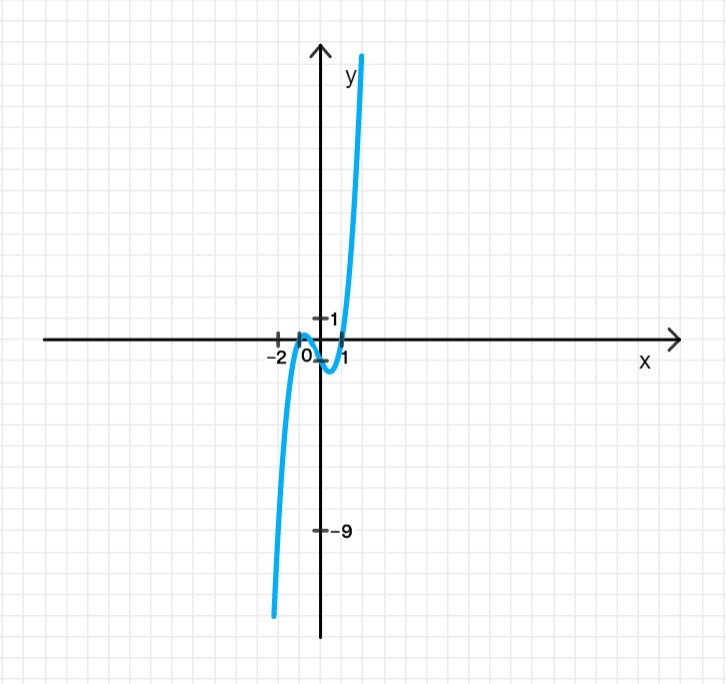
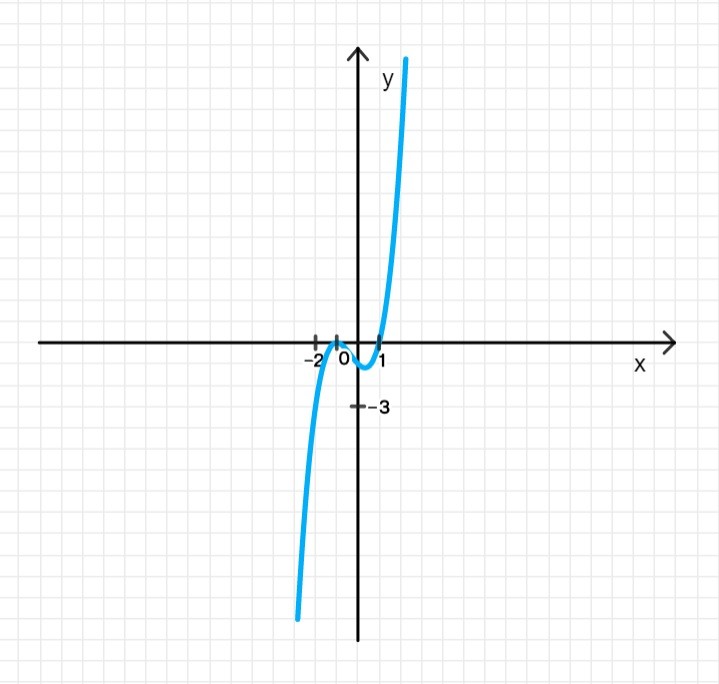
График функции:
Ответ: возрастает на ;
убывает на ;
— точка максимума;
— точка минимума.
б) ;
;
;
Промежуток возрастания:
;
, тогда:
и ;
;
;
Вершины функции:
;
;
Некоторые точки:
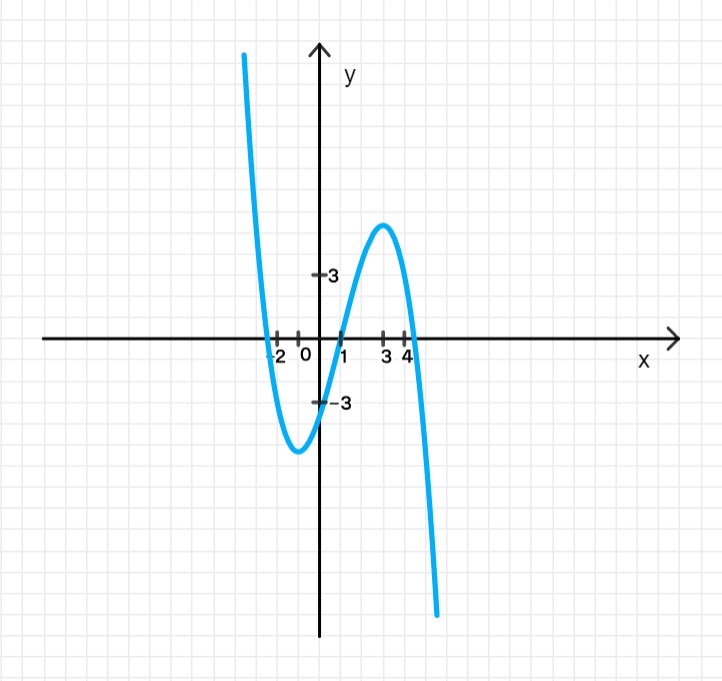
График функции:
Ответ: возрастает на и убывает на ;
— точка максимума;
— точка минимума.
в) ;
Промежуток возрастания:
;
, тогда:
и ;
;
или ;
Вершины функции:
;
;
Некоторые точки:
График функции:
Ответ: возрастает на и убывает на ;
— точка максимума;
— точка минимума.
г) ;
;
;
Промежуток возрастания:
;
, тогда:
и ;
;
или ;
Промежуток возрастания:
или ;
Вершины функции:
;
;
Некоторые точки:
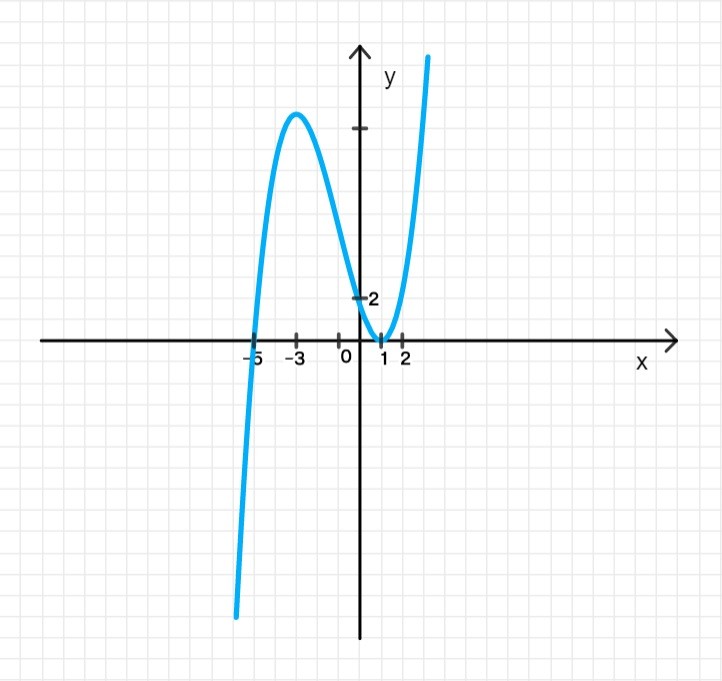
График функции:
Ответ: возрастает на и убывает на ;
— точка максимума;
— точка минимума.
а)
1. Нахождение производной:
Для начала найдем первую производную функции . Используем стандартные правила дифференцирования для каждого слагаемого по отдельности:
- Производная по равна ,
- Производная по равна ,
- Производная по равна ,
- Производная постоянной равна .
Применяем эти правила:
2. Промежутки возрастания и убывания:
Для нахождения промежутков возрастания и убывания исследуем знак первой производной .
Решим неравенство:
Разделим все на 2 для упрощения:
Для решения квадратного уравнения используем формулу дискриминанта:
Корни уравнения находим по формуле:
Приблизительные значения корней:
Теперь анализируем знак произведения .
Промежутки, на которых произведение положительное или ноль:
Таким образом, функция возрастает на промежутке и убывает на промежутке .
3. Вершины функции:
Для нахождения значений функции в точках и подставим их в исходное уравнение .
- В точке :
- В точке :
4. Некоторые точки функции:
Теперь определим значения функции для нескольких значений :
- Для :
- Для :
- Для :
Таблица значений:
5. График функции:
Функция имеет два экстремума: точку максимума в и точку минимума в .
Ответ:
- Функция возрастает на ,
- Функция убывает на ,
- Точка максимума: ,
- Точка минимума: .
б)
1. Нахождение производной:
Найдем первую производную функции:
2. Промежутки возрастания и убывания:
Теперь исследуем знак производной, решив неравенство .
Решим это квадратное уравнение:
Корни уравнения:
Таким образом, неравенство выполняется при .
3. Вершины функции:
Теперь найдем значения функции в точках и :
- В точке :
- В точке :
4. Некоторые точки функции:
Теперь определим значения функции для нескольких значений :
- Для :
- Для :
- Для :
- Для :
- Для :
Таблица значений:
5. График функции:
Ответ:
- Функция возрастает на ,
- Функция убывает на ,
- Точка максимума: ,
- Точка минимума: .
в)
1. Промежуток возрастания:
Для нахождения промежутков возрастания и убывания функции исследуем знак первой производной:
Решаем уравнение для нахождения корней:
Применяем метод знаков:
Промежутки:
2. Вершины функции:
Теперь вычислим значения функции в точках экстремума и :
- В точке :
- В точке :
3. Некоторые точки функции:
Таблица значений:
4. График функции:
Ответ:
- Функция возрастает на ,
- Функция убывает на ,
- Точка максимума: ,
- Точка минимума: .
г)
1. Нахождение производной:
Найдем первую производную функции:
2. Промежутки возрастания и убывания:
Для нахождения промежутков возрастания и убывания решим неравенство :
Корни уравнения:
Ответ:
- Функция возрастает на ,
- Функция убывает на .
3. Вершины функции:
Вычислим значения функции в точках и :
- В точке :
- В точке :
4. Некоторые точки функции:
Таблица значений:
5. График функции:
Ответ:
- Функция возрастает на ,
- Функция убывает на ,
- Точка максимума: ,
- Точка минимума: .