Краткий ответ:
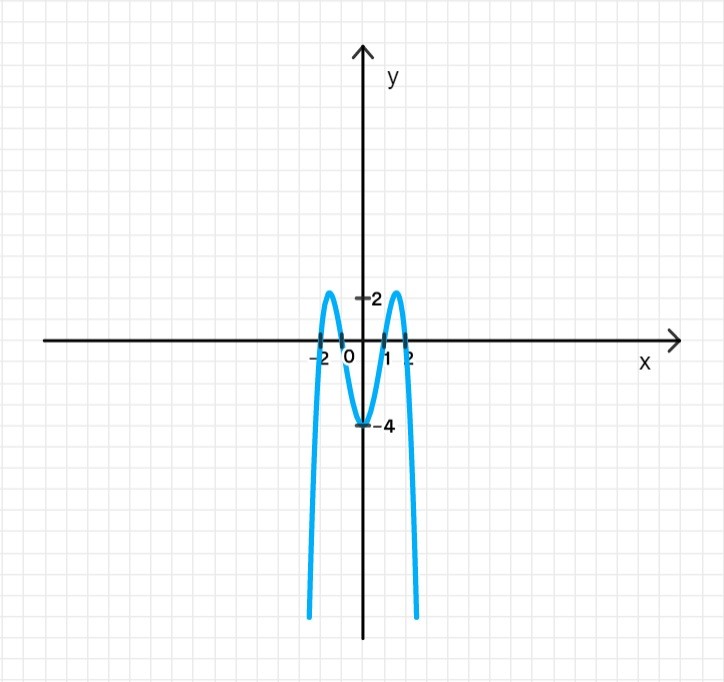
а) y = − x 4 + 5 x 2 − 4 y = -x^4 + 5x^2 — 4
y ′ = − ( x 4 ) ′ + 5 ( x 2 ) ′ − ( 4 ) ′ y’ = -(x^4)’ + 5(x^2)’ — (4)’ y ′ = − 4 x 3 + 5 ⋅ 2 x − 0 = 10 x − 4 x 3 y’ = -4x^3 + 5 \cdot 2x — 0 = 10x — 4x^3
Промежуток возрастания:10 x − 4 x 3 ≥ 0 10x — 4x^3 \geq 0 x ( 10 − 4 x 2 ) ≥ 0 x(10 — 4x^2) \geq 0 ( 10 + 2 x ) ⋅ x ⋅ ( 10 − 2 x ) ≥ 0 (\sqrt{10} + 2x) \cdot x \cdot (\sqrt{10} — 2x) \geq 0 x ≤ − 10 2 x \leq -\frac{\sqrt{10}}{2} 0 ≤ x ≤ 10 2 0 \leq x \leq \frac{\sqrt{10}}{2} x ≤ − 1 , 6 x \leq -1,6 0 ≤ x ≤ 1 , 6 0 \leq x \leq 1,6
Вершины функции:y ( ± 1 , 6 ) ≈ − 6 , 5 + 5 ⋅ 2 , 6 − 4 ≈ − 10 , 5 + 12 , 8 ≈ 2 , 3 y(\pm 1,6) \approx -6,5 + 5 \cdot 2,6 — 4 \approx -10,5 + 12,8 \approx 2,3 y ( 0 ) = − 0 4 + 5 ⋅ 0 2 − 4 = − 4 y(0) = -0^4 + 5 \cdot 0^2 — 4 = -4
Некоторые точки:
x − 2 − 1 1 2 y 0 0 0 0 \begin{array}{c|c c c c} x & -2 & -1 & 1 & 2 \\ \hline y & 0 & 0 & 0 & 0 \\ \end{array}
График функции:
Ответ: возрастает на ( − ∞ ; − 10 2 ] ∪ [ 0 ; 10 2 ] \left( -\infty; -\frac{\sqrt{10}}{2} \right] \cup \left[ 0; \frac{\sqrt{10}}{2} \right] [ − 10 2 ; 0 ] ∪ [ 10 2 ; + ∞ ) \left[ -\frac{\sqrt{10}}{2}; 0 \right] \cup \left[ \frac{\sqrt{10}}{2}; +\infty \right) x = ± 10 2 x = \pm \frac{\sqrt{10}}{2} x = 0 x = 0
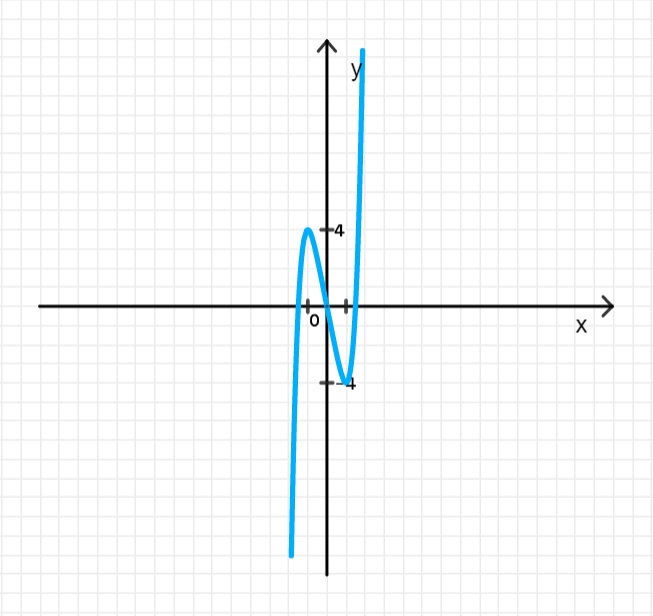
б) y = x 5 − 5 x y = x^5 — 5x
y ′ = ( x 5 ) ′ − ( 5 x ) ′ = 5 x 4 − 5 y’ = (x^5)’ — (5x)’ = 5x^4 — 5
Промежуток возрастания:5 x 4 − 5 ≥ 0 5x^4 — 5 \geq 0 x 4 ≥ 1 x^4 \geq 1 x ≤ − 1 x \leq -1 x ≥ 1 x \geq 1
Вершины функции:y ( − 1 ) = ( − 1 ) 5 − 5 ⋅ ( − 1 ) = − 1 + 5 = 4 y(-1) = (-1)^5 — 5 \cdot (-1) = -1 + 5 = 4 y ( 1 ) = 1 5 − 5 ⋅ 1 = 1 − 5 = − 4 y(1) = 1^5 — 5 \cdot 1 = 1 — 5 = -4
Некоторые точки:
x − 1 , 5 0 1 , 5 y 0 0 0 \begin{array}{c|c c c} x & -1,5 & 0 & 1,5 \\ \hline y & 0 & 0 & 0 \\ \end{array}
График функции:
Ответ: возрастает на ( − ∞ ; − 1 ] ∪ [ 1 ; + ∞ ) (-\infty; -1] \cup [1; +\infty) [ − 1 ; 1 ] [-1; 1] x = − 1 x = -1 x = 1 x = 1
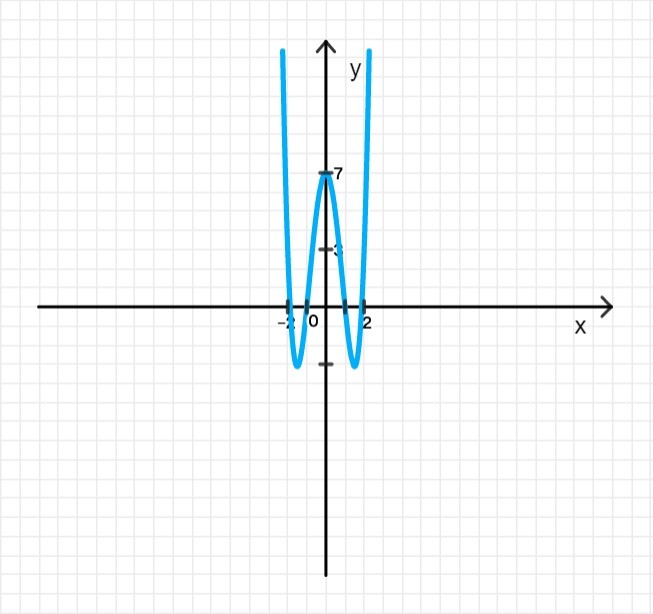
в) y = 2 x 4 − 9 x 2 + 7 y = 2x^4 — 9x^2 + 7
y ′ = 2 ( x 4 ) ′ − 9 ( x 2 ) ′ + ( 7 ) ′ y’ = 2(x^4)’ — 9(x^2)’ + (7)’ y ′ = 2 ⋅ 4 x 3 − 9 ⋅ 2 x + 0 = 8 x 3 − 18 x y’ = 2 \cdot 4x^3 — 9 \cdot 2x + 0 = 8x^3 — 18x
Промежуток возрастания:8 x 3 − 18 x ≥ 0 8x^3 — 18x \geq 0 2 x ( 4 x 2 − 9 ) ≥ 0 2x(4x^2 — 9) \geq 0 ( 2 x + 3 ) ⋅ x ⋅ ( 2 x − 3 ) ≥ 0 (2x + 3) \cdot x \cdot (2x — 3) \geq 0 − 1 , 5 ≤ x ≤ 0 -1,5 \leq x \leq 0 x ≥ 1 , 5 x \geq 1,5
Вершины функции:y ( ± 1 , 5 ) ≈ 2 ⋅ 5 , 06 − 9 ⋅ 2 , 25 + 7 ≈ 10 , 1 − 20 , 25 + 7 ≈ − 3 , 15 y(\pm 1,5) \approx 2 \cdot 5,06 — 9 \cdot 2,25 + 7 \approx 10,1 — 20,25 + 7 \approx -3,15 y ( 0 ) = 2 ⋅ 0 4 − 9 ⋅ 0 2 + 7 = 7 y(0) = 2 \cdot 0^4 — 9 \cdot 0^2 + 7 = 7
Некоторые точки:
x − 2 − 1 1 2 y 3 0 0 3 \begin{array}{c|c c c c} x & -2 & -1 & 1 & 2 \\ \hline y & 3 & 0 & 0 & 3 \\ \end{array}
График функции:
Ответ: возрастает на [ − 1 , 5 ; 0 ] ∪ [ 1 , 5 ; + ∞ ) [-1,5; 0] \cup [1,5; +\infty) ( − ∞ ; − 1 , 5 ] ∪ [ 0 ; 1 , 5 ] (-\infty; -1,5] \cup [0; 1,5] x = 0 x = 0 x = ± 1 , 5 x = \pm 1,5
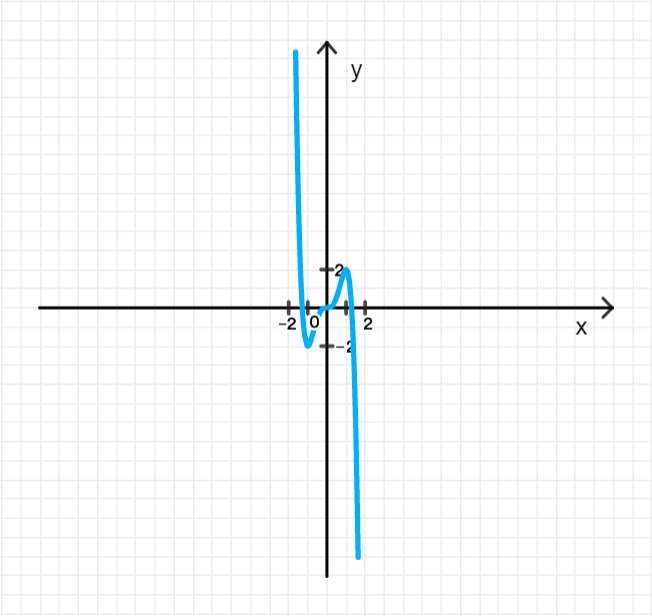
г) y = 5 x 3 − 3 x 5 y = 5x^3 — 3x^5
y ′ = 5 ( x 3 ) ′ − 3 ( x 5 ) ′ = 5 ⋅ 3 x 2 − 3 ⋅ 5 x 4 = 15 x 2 − 15 x 4 y’ = 5(x^3)’ — 3(x^5)’ = 5 \cdot 3x^2 — 3 \cdot 5x^4 = 15x^2 — 15x^4
Промежуток возрастания:15 x 2 − 15 x 4 ≥ 0 15x^2 — 15x^4 \geq 0 x 2 − x 4 ≥ 0 x^2 — x^4 \geq 0 x 2 ( 1 − x 2 ) ≥ 0 x^2(1 — x^2) \geq 0 1 − x 2 ≥ 0 1 — x^2 \geq 0 1 ≥ x 2 1 \geq x^2 − 1 ≤ x ≤ 1 -1 \leq x \leq 1 x = 0 x = 0
Вершины функции:y ( − 1 ) = 5 ⋅ ( − 1 ) 3 − 3 ⋅ ( − 1 ) 5 = − 5 + 3 = − 2 y(-1) = 5 \cdot (-1)^3 — 3 \cdot (-1)^5 = -5 + 3 = -2 y ( 1 ) = 5 ⋅ 1 3 − 3 ⋅ 1 5 = 5 − 3 = 2 y(1) = 5 \cdot 1^3 — 3 \cdot 1^5 = 5 — 3 = 2
Некоторые точки:
x − 1 , 5 0 1 , 5 y 5 , 9 0 5 , 9 \begin{array}{c|c c c} x & -1,5 & 0 & 1,5 \\ \hline y & 5,9 & 0 & 5,9 \\ \end{array}
График функции:
Ответ: возрастает на [ − 1 ; 1 ] [-1; 1] ( − ∞ ; − 1 ] ∪ [ 1 ; + ∞ ) (-\infty; -1] \cup [1; +\infty) x = 1 x = 1 x = − 1 x = -1
Подробный ответ:
а) y = − x 4 + 5 x 2 − 4 y = -x^4 + 5x^2 — 4
1. Нахождение производной:
Найдем первую производную функции y = − x 4 + 5 x 2 − 4 y = -x^4 + 5x^2 — 4
Производная x 4 x^4 x x 4 x 3 4x^3 Производная 5 x 2 5x^2 x x 10 x 10x Производная постоянной − 4 -4 0 0 Таким образом, производная будет:
y ′ = − ( x 4 ) ′ + 5 ( x 2 ) ′ − ( 4 ) ′ = − 4 x 3 + 10 x y’ = -(x^4)’ + 5(x^2)’ — (4)’ = -4x^3 + 10x
Получили первую производную:
y ′ = − 4 x 3 + 10 x y’ = -4x^3 + 10x
2. Промежутки возрастания и убывания:
Чтобы найти промежутки возрастания и убывания функции, решим неравенство для производной y ′ = − 4 x 3 + 10 x y’ = -4x^3 + 10x
− 4 x 3 + 10 x ≥ 0 -4x^3 + 10x \geq 0
Выносим общий множитель − 2 x -2x
− 2 x ( 2 x 2 − 5 ) ≥ 0 -2x(2x^2 — 5) \geq 0
Решаем неравенство. Для этого нам нужно решить:
x ( 5 − 2 x 2 ) ≥ 0 x(5 — 2x^2) \geq 0
Решаем это неравенство поэтапно:
x ≥ 0 x \geq 0 x ≤ 0 x \leq 0 x x 5 − 2 x 2 ≥ 0 5 — 2x^2 \geq 0 x 2 ≤ 5 2 x^2 \leq \frac{5}{2} x ≤ ± 5 2 ≈ ± 1.58 x \leq \pm \sqrt{\frac{5}{2}} \approx \pm 1.58 Итак, получаем промежутки:
x ≤ − 10 2 или 0 ≤ x ≤ 10 2 (при 10 ≈ 3.16 ) x \leq -\frac{\sqrt{10}}{2} \quad \text{или} \quad 0 \leq x \leq \frac{\sqrt{10}}{2} \quad \text{(при \( \sqrt{10} \approx 3.16 \))}
Здесь видно, что функция возрастает на промежутке ( − ∞ ; − 10 2 ] ∪ [ 0 ; 10 2 ] \left( -\infty; -\frac{\sqrt{10}}{2} \right] \cup \left[ 0; \frac{\sqrt{10}}{2} \right] [ − 10 2 ; 0 ] ∪ [ 10 2 ; + ∞ ) \left[ -\frac{\sqrt{10}}{2}; 0 \right] \cup \left[ \frac{\sqrt{10}}{2}; +\infty \right)
3. Вершины функции:
Теперь находим значения функции в точках экстремума, то есть в точках x = 0 x = 0 x = ± 10 2 x = \pm \frac{\sqrt{10}}{2}
y ( 0 ) = − ( 0 ) 4 + 5 ⋅ 0 2 − 4 = − 4 y(0) = -(0)^4 + 5 \cdot 0^2 — 4 = -4
В точке x = ± 1.6 x = \pm 1.6 y ( ± 1.6 ) ≈ − ( 1.6 ) 4 + 5 ⋅ ( 1.6 ) 2 − 4 =
= − 6.5 + 5 ⋅ 2.6 − 4 ≈ − 10.5 + 12.8 ≈ 2.3 y(\pm 1.6) \approx -(1.6)^4 + 5 \cdot (1.6)^2 — 4 = -6.5 + 5 \cdot 2.6 — 4 \approx -10.5 + 12.8 \approx 2.3
Таким образом, в точке x = 0 x = 0 y = − 4 y = -4 x = ± 1.6 x = \pm 1.6 y ≈ 2.3 y \approx 2.3
4. Некоторые точки функции:
Для получения графика определим несколько точек:
x − 2 − 1 1 2 y 0 0 0 0 \begin{array}{|c|c|c|c|c} \hline x & -2 & -1 & 1 & 2 \\ \hline y & 0 & 0 & 0 & 0 \\ \hline \end{array}
5. График функции:
Функция будет иметь два экстремума: точку максимума при x = − 1.6 x = -1.6 x = 1.6 x = 1.6 x = 0 x = 0
Ответ:
Функция возрастает на ( − ∞ ; − 10 2 ] ∪ [ 0 ; 10 2 ] \left( -\infty; -\frac{\sqrt{10}}{2} \right] \cup \left[ 0; \frac{\sqrt{10}}{2} \right] Функция убывает на [ − 10 2 ; 0 ] ∪ [ 10 2 ; + ∞ ) \left[ -\frac{\sqrt{10}}{2}; 0 \right] \cup \left[ \frac{\sqrt{10}}{2}; +\infty \right) Точка максимума: x = ± 10 2 x = \pm \frac{\sqrt{10}}{2} Точка минимума: x = 0 x = 0 б) y = x 5 − 5 x y = x^5 — 5x
1. Нахождение производной:
Найдем первую производную функции:
y ′ = ( x 5 ) ′ − ( 5 x ) ′ = 5 x 4 − 5 y’ = (x^5)’ — (5x)’ = 5x^4 — 5
2. Промежутки возрастания и убывания:
Теперь решим неравенство для производной y ′ = 5 x 4 − 5 y’ = 5x^4 — 5
5 x 4 − 5 ≥ 0 5x^4 — 5 \geq 0 x 4 ≥ 1 x^4 \geq 1
Это неравенство выполняется, когда x ≤ − 1 x \leq -1 x ≥ 1 x \geq 1
Таким образом, функция возрастает на ( − ∞ ; − 1 ] ∪ [ 1 ; + ∞ ) (-\infty; -1] \cup [1; +\infty) [ − 1 ; 1 ] [-1; 1]
3. Вершины функции:
Теперь находим значения функции в точках экстремума x = − 1 x = -1 x = 1 x = 1
y ( − 1 ) = ( − 1 ) 5 − 5 ⋅ ( − 1 ) = − 1 + 5 = 4 y(-1) = (-1)^5 — 5 \cdot (-1) = -1 + 5 = 4
y ( 1 ) = 1 5 − 5 ⋅ 1 = 1 − 5 = − 4 y(1) = 1^5 — 5 \cdot 1 = 1 — 5 = -4
4. Некоторые точки функции:
Для получения графика определим несколько точек:
x − 1 , 5 0 1 , 5 y 0 0 0 \begin{array}{|c|c|c|c} \hline x & -1,5 & 0 & 1,5 \\ \hline y & 0 & 0 & 0 \\ \hline \end{array}
5. График функции:
Функция имеет два экстремума: точку максимума при x = − 1 x = -1 x = 1 x = 1
Ответ:
Функция возрастает на ( − ∞ ; − 1 ] ∪ [ 1 ; + ∞ ) (-\infty; -1] \cup [1; +\infty) Функция убывает на [ − 1 ; 1 ] [-1; 1] Точка максимума: x = − 1 x = -1 Точка минимума: x = 1 x = 1 в) y = 2 x 4 − 9 x 2 + 7 y = 2x^4 — 9x^2 + 7
1. Нахождение производной:
Найдем первую производную функции:
y ′ = 2 ( x 4 ) ′ − 9 ( x 2 ) ′ + ( 7 ) ′ y’ = 2(x^4)’ — 9(x^2)’ + (7)’ y ′ = 2 ⋅ 4 x 3 − 9 ⋅ 2 x + 0 = 8 x 3 − 18 x y’ = 2 \cdot 4x^3 — 9 \cdot 2x + 0 = 8x^3 — 18x
2. Промежутки возрастания и убывания:
Решим неравенство для производной:
8 x 3 − 18 x ≥ 0 8x^3 — 18x \geq 0 2 x ( 4 x 2 − 9 ) ≥ 0 2x(4x^2 — 9) \geq 0
Решаем это неравенство:
( 2 x + 3 ) ⋅ x ⋅ ( 2 x − 3 ) ≥ 0 (2x + 3) \cdot x \cdot (2x — 3) \geq 0
Это неравенство выполняется на промежутках:
− 1.5 ≤ x ≤ 0 или x ≥ 1.5 -1.5 \leq x \leq 0 \quad \text{или} \quad x \geq 1.5
3. Вершины функции:
Теперь вычислим значения функции в точках x = − 1.5 x = -1.5 x = 0 x = 0 x = 1.5 x = 1.5
y ( − 1.5 ) ≈ 2 ⋅ 5.06 − 9 ⋅ 2.25 + 7 ≈ 10.1 − 20.25 + 7 ≈ − 3.15 y(-1.5) \approx 2 \cdot 5.06 — 9 \cdot 2.25 + 7 \approx 10.1 — 20.25 + 7 \approx -3.15
y ( 0 ) = 2 ⋅ 0 4 − 9 ⋅ 0 2 + 7 = 7 y(0) = 2 \cdot 0^4 — 9 \cdot 0^2 + 7 = 7
y ( 1.5 ) ≈ 2 ⋅ 5.06 − 9 ⋅ 2.25 + 7 ≈ − 3.15 y(1.5) \approx 2 \cdot 5.06 — 9 \cdot 2.25 + 7 \approx -3.15
4. Некоторые точки функции:
Для построения графика:
x − 2 − 1 1 2 y 3 0 0 3 \begin{array}{|c|c|c|c|c} \hline x & -2 & -1 & 1 & 2 \\ \hline y & 3 & 0 & 0 & 3 \\ \hline \end{array}
5. График функции:
Ответ:
Функция возрастает на [ − 1.5 ; 0 ] ∪ [ 1.5 ; + ∞ ) [-1.5; 0] \cup [1.5; +\infty) Функция убывает на ( − ∞ ; − 1.5 ] ∪ [ 0 ; 1.5 ] (-\infty; -1.5] \cup [0; 1.5] Точка максимума: x = 0 x = 0 Точка минимума: x = ± 1.5 x = \pm 1.5 г) y = 5 x 3 − 3 x 5 y = 5x^3 — 3x^5
1. Нахождение производной:
Найдем первую производную функции:
y ′ = 5 ( x 3 ) ′ − 3 ( x 5 ) ′ = 5 ⋅ 3 x 2 − 3 ⋅ 5 x 4 = 15 x 2 − 15 x 4 y’ = 5(x^3)’ — 3(x^5)’ = 5 \cdot 3x^2 — 3 \cdot 5x^4 = 15x^2 — 15x^4
2. Промежуток возрастания и убывания:
Решим неравенство для производной:
15 x 2 − 15 x 4 ≥ 0 15x^2 — 15x^4 \geq 0 x 2 − x 4 ≥ 0 x^2 — x^4 \geq 0 x 2 ( 1 − x 2 ) ≥ 0 x^2(1 — x^2) \geq 0
Это неравенство выполняется на промежутках:
− 1 ≤ x ≤ 1 или x = 0 -1 \leq x \leq 1 \quad \text{или} \quad x = 0
3. Вершины функции:
Вычислим значения функции в точках x = − 1 x = -1 x = 1 x = 1
y ( − 1 ) = 5 ⋅ ( − 1 ) 3 − 3 ⋅ ( − 1 ) 5 = − 5 + 3 = − 2 y(-1) = 5 \cdot (-1)^3 — 3 \cdot (-1)^5 = -5 + 3 = -2
y ( 1 ) = 5 ⋅ 1 3 − 3 ⋅ 1 5 = 5 − 3 = 2 y(1) = 5 \cdot 1^3 — 3 \cdot 1^5 = 5 — 3 = 2
4. Некоторые точки функции:
Для построения графика:
x − 1 , 5 0 1 , 5 y 5 , 9 0 5 , 9 \begin{array}{|c|c|c|c} \hline x & -1,5 & 0 & 1,5 \\ \hline y & 5,9 & 0 & 5,9 \\ \hline \end{array}
5. График функции:
Ответ:
Функция возрастает на [ − 1 ; 1 ] [-1; 1] Функция убывает на ( − ∞ ; − 1 ] ∪ [ 1 ; + ∞ ) (-\infty; -1] \cup [1; +\infty) Точка максимума: x = 1 x = 1 Точка минимума: x = − 1 x = -1