Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 44.68 Профильный Уровень Мордкович — Подробные Ответы
Исследуйте функцию на монотонность и экстремумы и постройте ее график:
а) ;
б) ;
в) ;
г)
а) ;
Промежуток возрастания:
Вершины функции:
Некоторые точки:
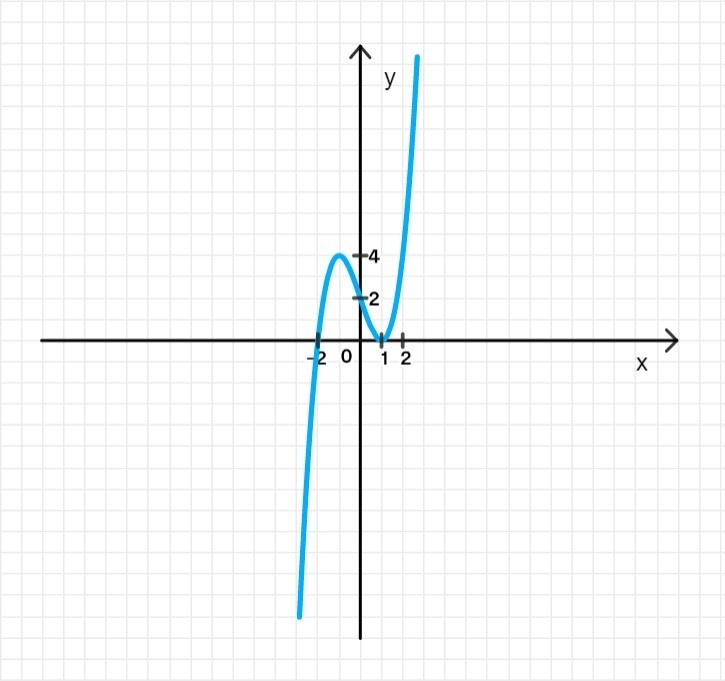
График функции:
Ответ: возрастает на и убывает на ;
— точка максимума;
— точка минимума.
б) ;
Промежуток возрастания:
Вершина функции:
Некоторые точки:
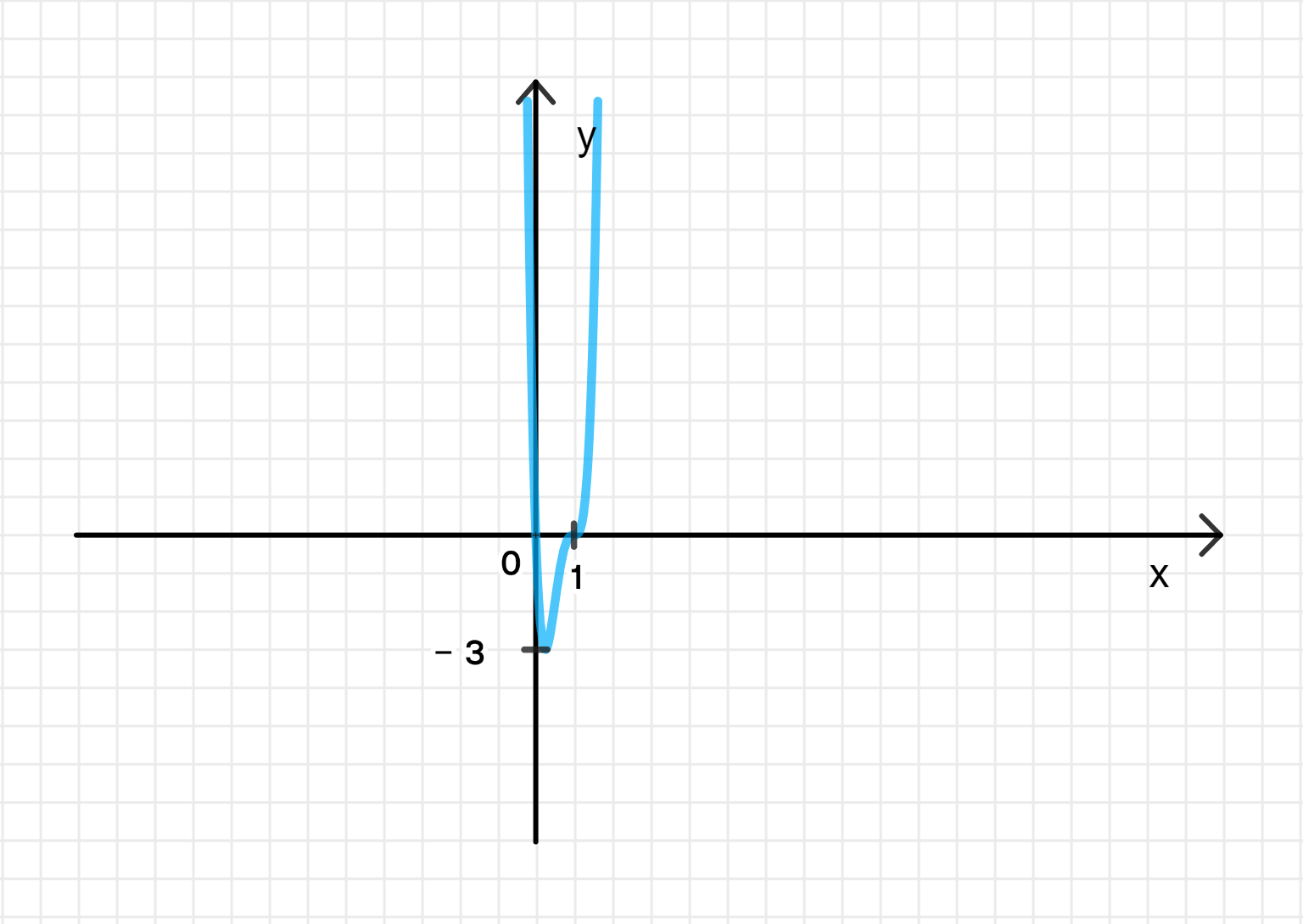
График функции:
Ответ: возрастает на и убывает на ;
— точка минимума.
в) ;
Промежуток возрастания:
Вершины функции:
Некоторые точки:
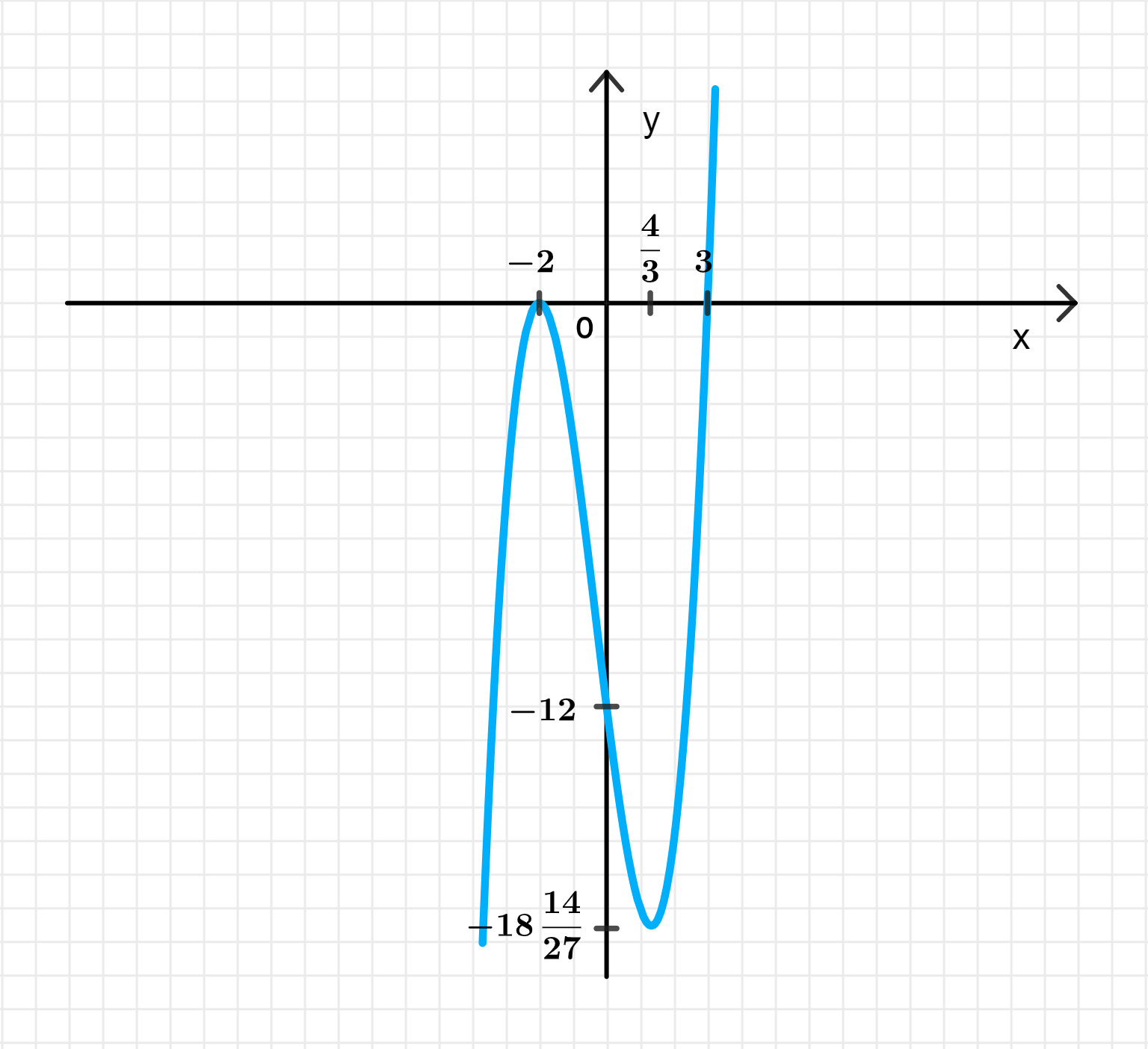
График функции:
Ответ: возрастает на и убывает на ;
— точка максимума;
— точка минимума.
г) ;
Промежуток возрастания:
Вершина функции:
Некоторые точки:
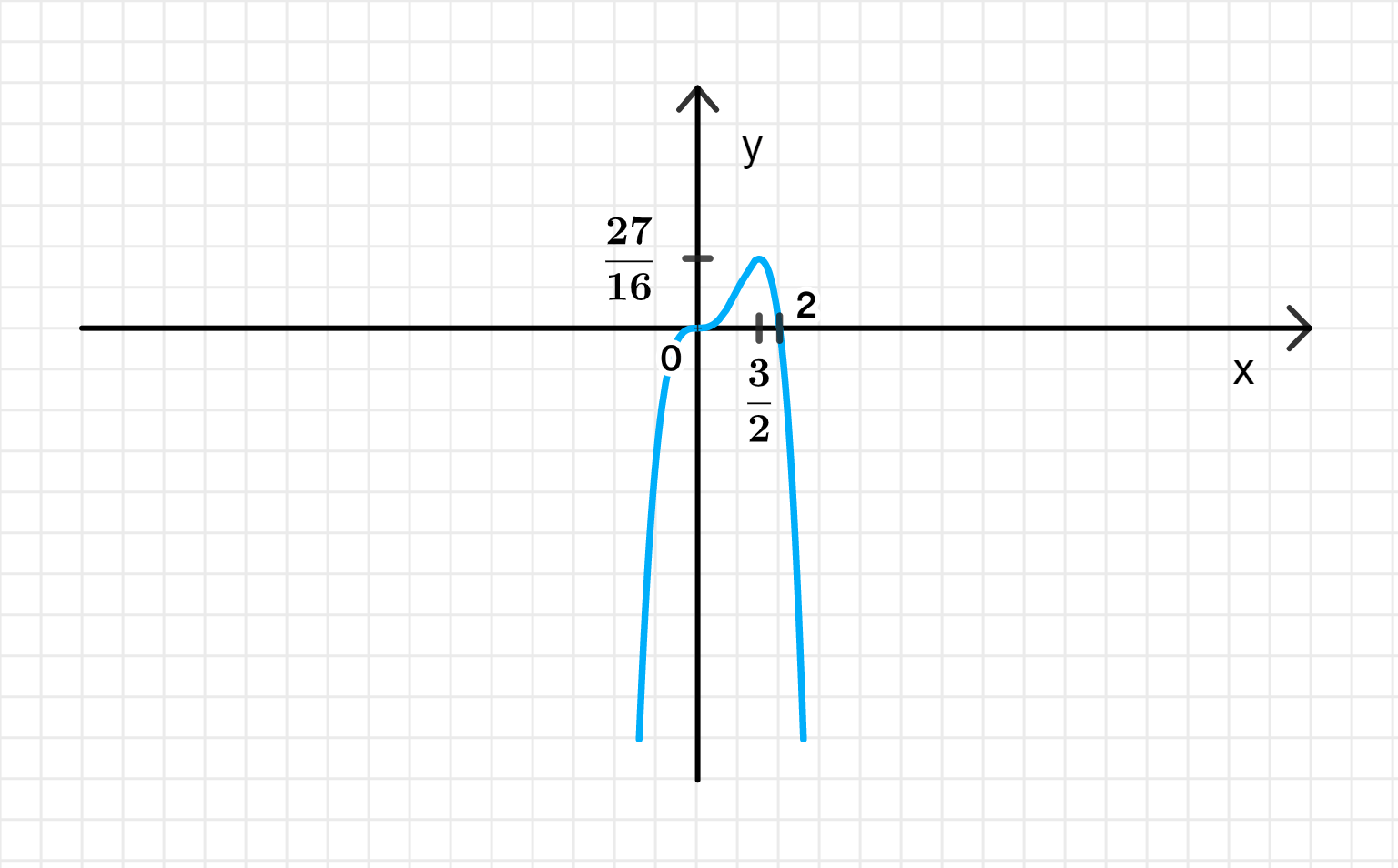
4) График функции:
Ответ: возрастает на и убывает на ;
— точка максимума.
а)
1. Нахождение производной:
Начнем с нахождения первой производной функции . Для этого используем правило дифференцирования произведения:
Для каждого множителя:
- Производная по равна ,
- Производная по равна 1.
Подставляем эти производные:
Теперь упрощаем:
Раскроем скобки:
Итак, производная:
2. Промежутки возрастания и убывания:
Для нахождения промежутков возрастания и убывания решим неравенство для первой производной:
Разделим обе части на 3:
Это неравенство можно решить, записав его в виде:
Итак, функция возрастает или убывает на следующих промежутках:
Таким образом, функция возрастает на промежутке и убывает на промежутке .
3. Вершины функции:
Теперь находим значения функции в точках экстремума. Эти точки могут быть на и .
- В точке :
- В точке :
4. Некоторые точки функции:
Для построения графика вычислим значения функции для нескольких точек:
5. График функции:
Функция будет возрастать на и убывать на . В точке находится точка максимума, а в точке — точка минимума.
Ответ:
- Функция возрастает на ,
- Функция убывает на ,
- — точка максимума,
- — точка минимума.
б)
1. Нахождение производной:
Найдем первую производную функции по правилу дифференцирования произведения:
Производная по равна . Тогда:
2. Промежуток возрастания и убывания:
Решим неравенство для первой производной:
Делим обе части на (так как оно всегда положительно):
Теперь решаем неравенство:
- для всех ,
- , то есть .
Таким образом, функция возрастает на промежутке , и убывает на .
3. Вершина функции:
Для нахождения вершины функции подставим в уравнение:
4. Некоторые точки функции:
Для построения графика вычислим несколько значений функции:
5. График функции:
Ответ:
- Функция возрастает на ,
- Функция убывает на ,
- — точка минимума.
в)
1. Нахождение производной:
Найдем первую производную функции по правилу дифференцирования произведения:
- Производная по равна ,
- Производная по равна 1.
Тогда:
2. Промежуток возрастания и убывания:
Решим неравенство для первой производной:
Вычислим дискриминант:
Корни уравнения:
Неравенство выполняется, когда:
3. Вершины функции:
Подставляем найденные значения и в исходное уравнение:
- В точке :
- В точке :
4. Некоторые точки функции:
Для построения графика вычислим несколько значений функции:
5. График функции:
Ответ:
- Функция возрастает на ,
- Функция убывает на ,
- — точка максимума,
- — точка минимума.
г)
1. Нахождение производной:
Найдем первую производную функции:
2. Промежуток возрастания и убывания:
Решим неравенство для первой производной:
Выносим :
Решаем это неравенство:
3. Вершина функции:
Подставляем в уравнение:
4. Некоторые точки функции:
Для построения графика:
5. График функции:
Ответ:
- Функция возрастает на ,
- Функция убывает на ,
- — точка максимума.