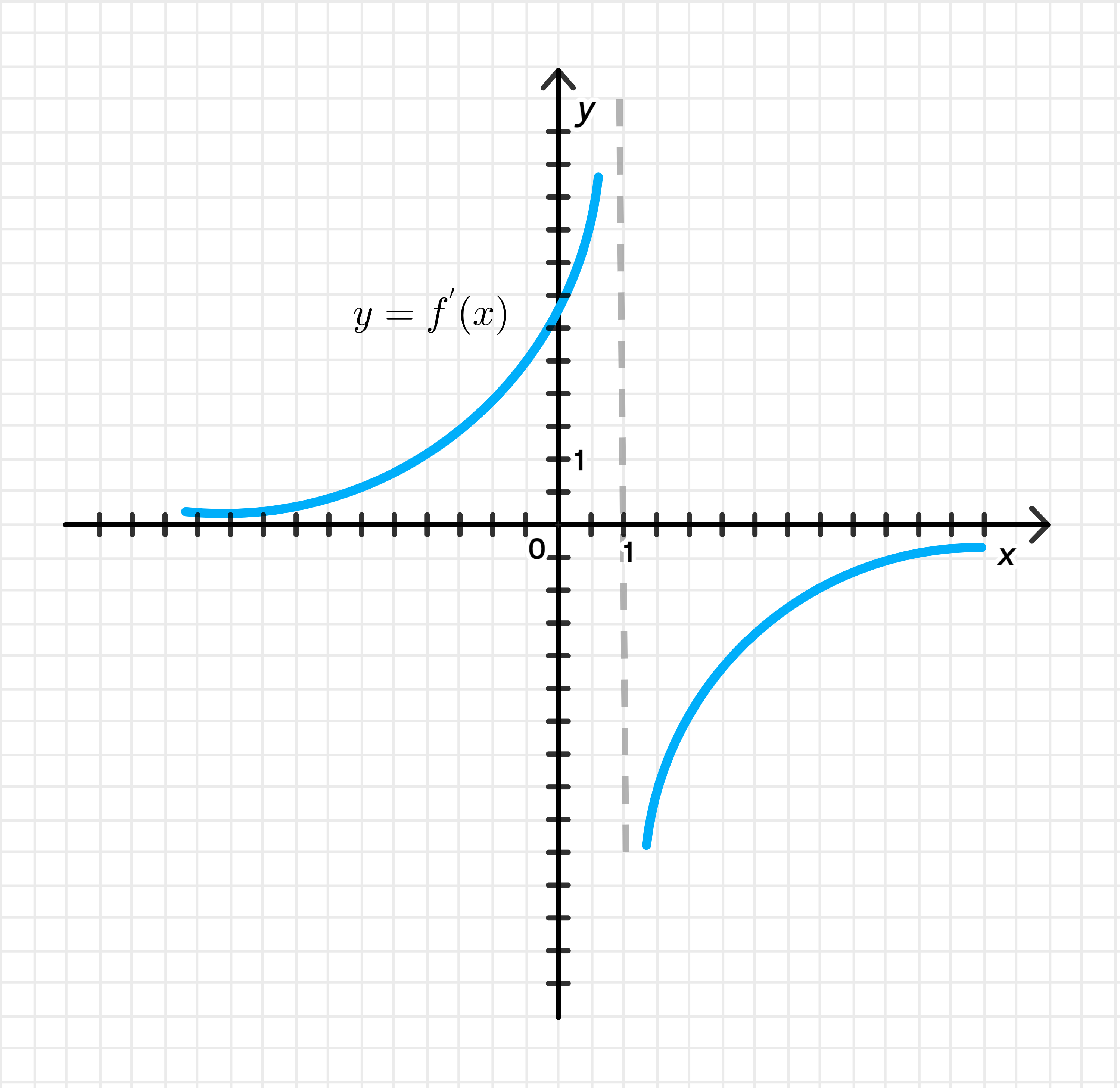Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 44.8 Профильный Уровень Мордкович — Подробные Ответы
а) Изобразите эскиз графика производной функции , если известно, что данная функция возрастает на и убывает на промежутке .
б) Изобразите эскиз графика производной функции , если известно, что данная функция убывает на луче , возрастает на отрезке , убывает на луче .
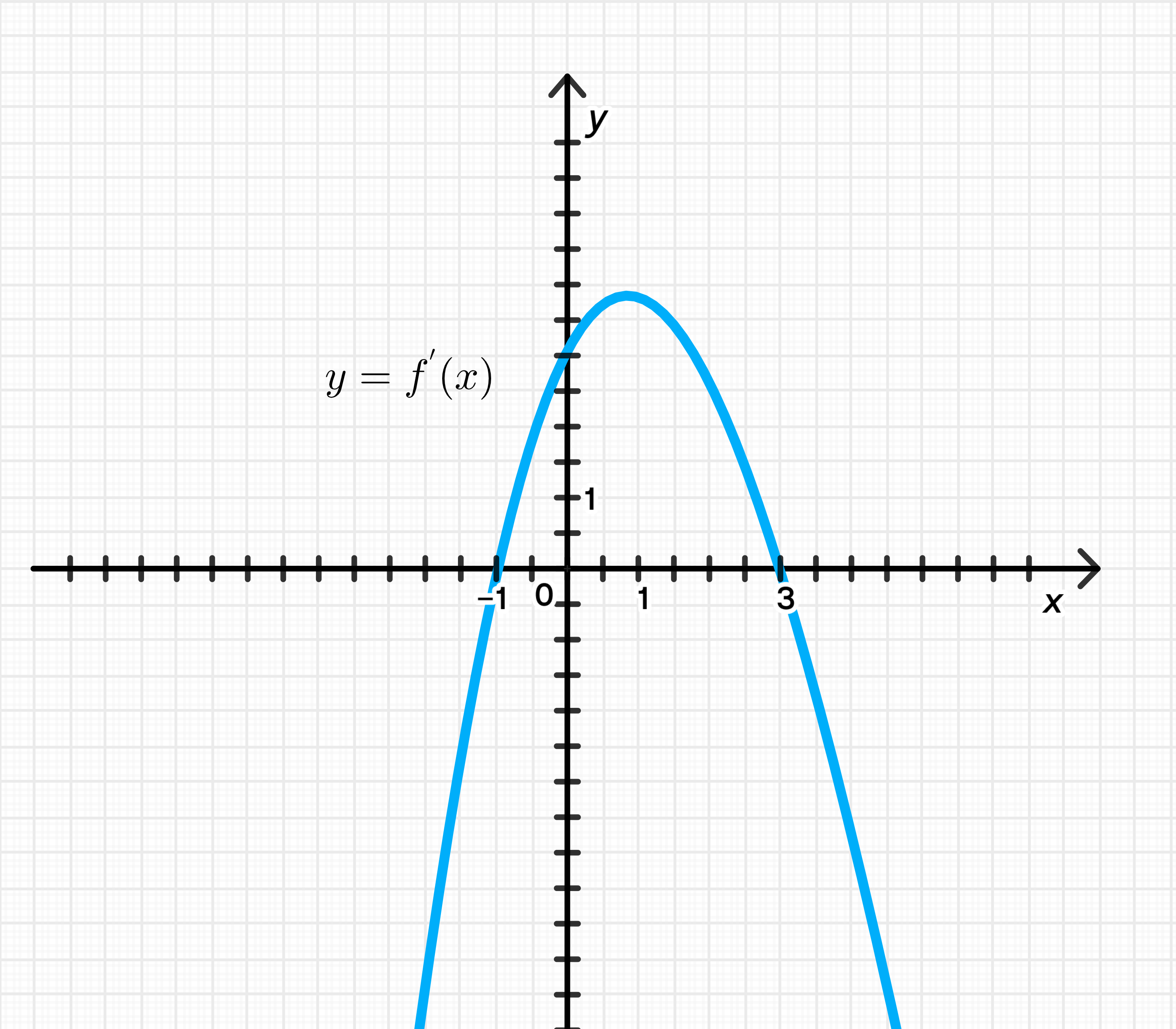
а) Эскиз графика производной функции возрастающей на и убывающей на :
б) Эскиз графика производной функции возрастающей на и убывающей на :
Прежде чем решать, напомним ключевое:
- Если возрастает на интервале, то на этом интервале.
- Если убывает, то .
- Если в точке функция переходит от возрастания к убыванию (или наоборот), это указывает на локальный экстремум функции, а значит, в этой точке.
а)
Эскиз графика производной функции , возрастающей на и убывающей на .
Шаг 1: Анализ поведения функции
- возрастает на → значит, на
- убывает на → значит, на
- В точке происходит переход от возрастания к убыванию, значит:
- Это локальный максимум функции
Шаг 2: Построение графика производной
- График положителен на
- График в точке
- График на
Это означает, что график производной проходит через точку (1; 0), находится выше оси x слева от неё и ниже оси x справа.
б)
Эскиз графика производной функции , возрастающей на и убывающей на .
Шаг 1: Анализ поведения функции
- убывает на → на этом луче
- возрастает на → на этом отрезке
- убывает на → на этом луче
Переходы:
- В точке : переход от убывания к возрастанию → минимум →
- В точке : переход от возрастания к убыванию → максимум →
Шаг 2: Построение графика производной
- На :
- В точке :
- На :
- В точке :
- На :
То есть график производной:
- Отрицательный до
- Пересекает ось x в
- Положительный между и
- Пересекает ось x снова в
- Отрицательный после
Итог: