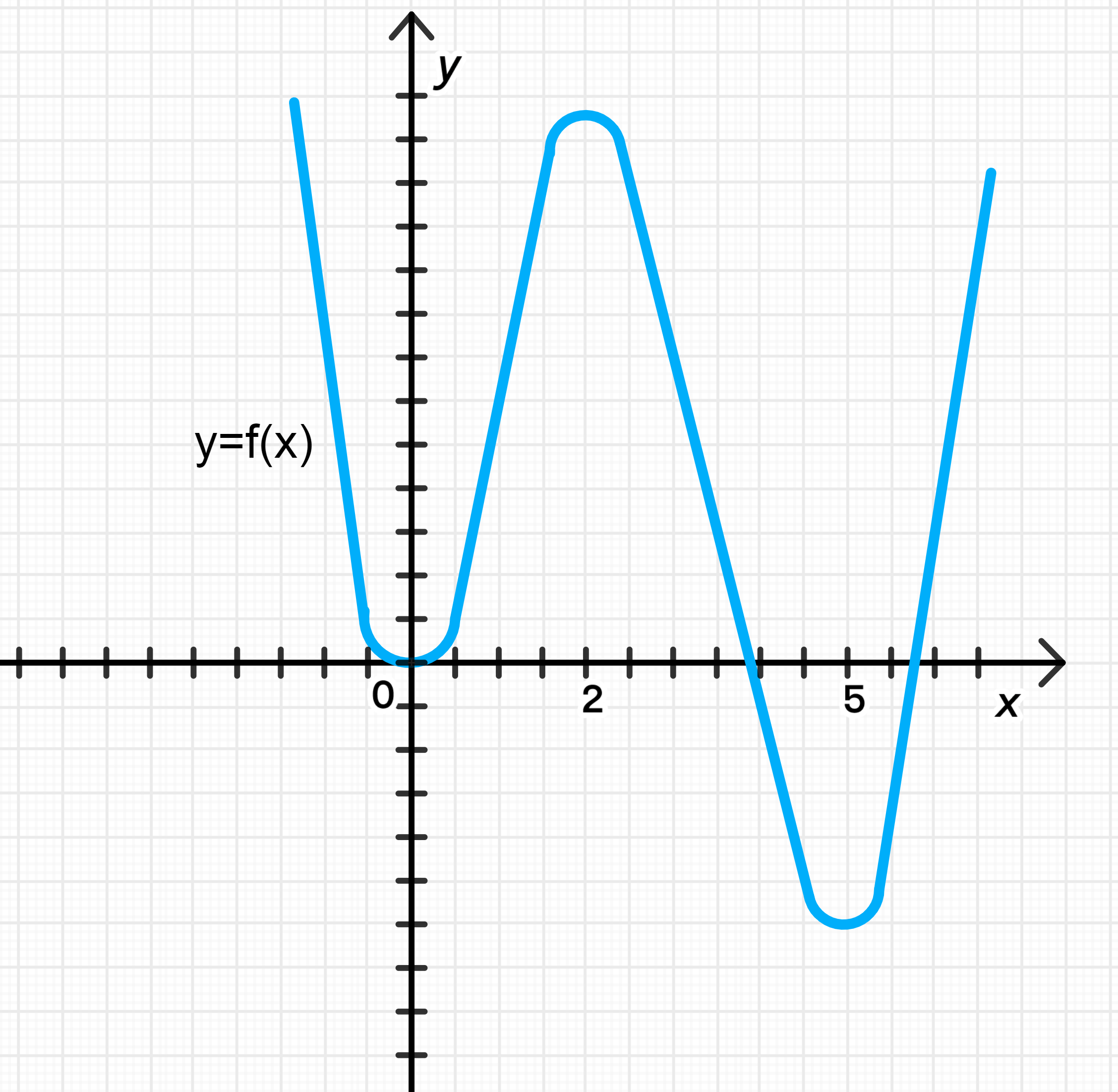ГДЗ по Алгебре 10 Класс Номер 44.9 Профильный Уровень Мордкович — Подробные Ответы

Изобразите эскиз графика функции $y = f(x)$, если промежутки постоянства знака производной $f'(x)$ представлены на схеме:

а) рис. 113;

б) рис. 114;

в) рис. 115;

г) рис. 116.

а) Рисунок 113:

б) Рисунок 114:

в) Рисунок 115:

г) Рисунок 116:

Основная идея

• $f'(x) > 0$ — функция возрастает.
• $f'(x) < 0$ — функция убывает.
• В точке перехода знака производной (если она есть) может быть экстремум:
  • $f'(x)$ меняется с + на − → максимум.
  • $f'(x)$ меняется с − на + → минимум.
  • Если знак не меняется, то экстремума нет.

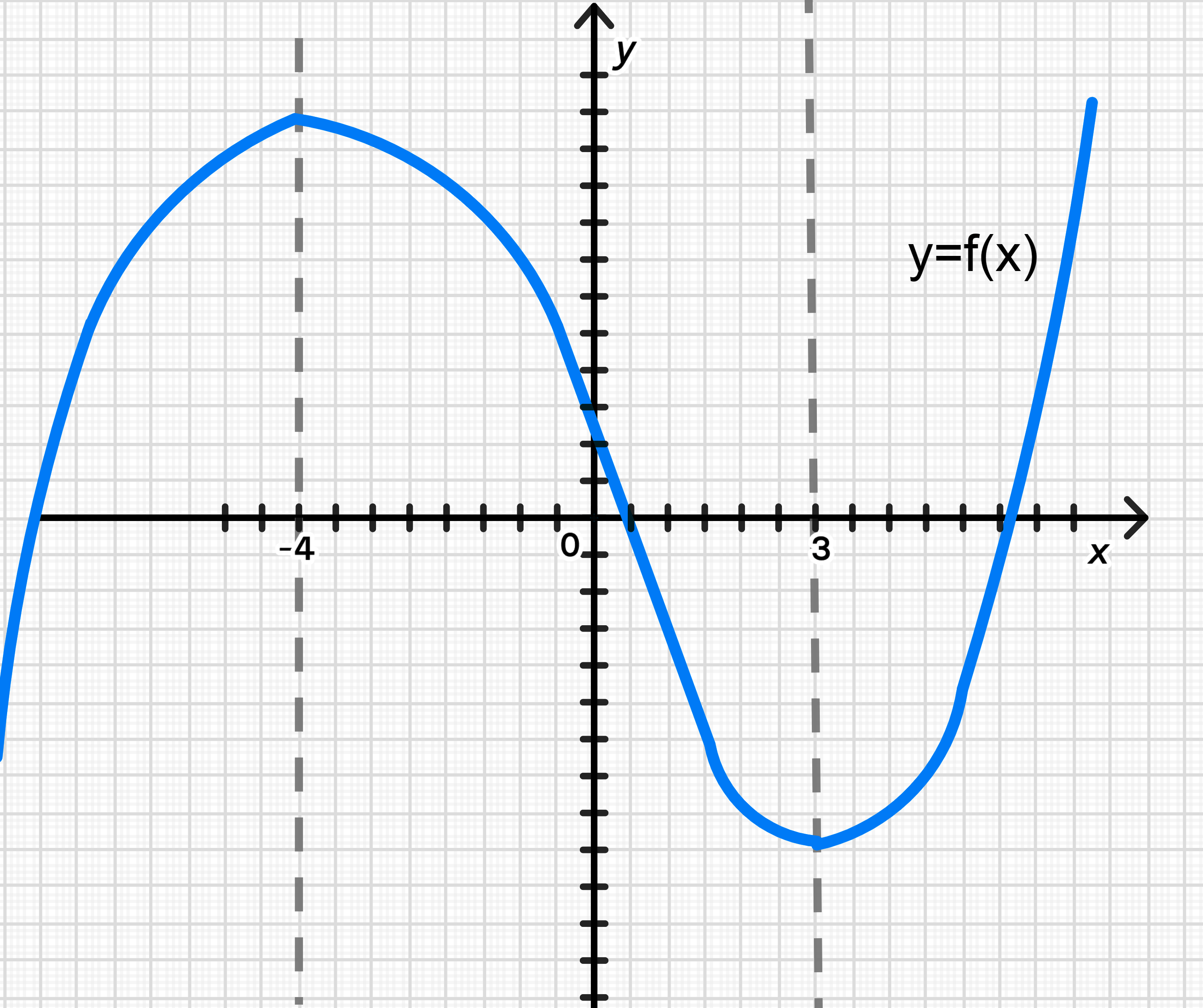
а) Рис. 113

$$f^{\mathrm{\prime }}(x)>0\text{ при }x<-4,f^{\mathrm{\prime }}(x)<0\text{ при }-4<x<3,$$

$$f'(x) > 0 \text{ при } x < -4,\quad f'(x) < 0 \text{ при } -4 < x < 3,\quad f'(x) > 0 \text{ при } x > 3$$

Пошаговое рассуждение:

1. На интервале $x < -4$: $f'(x) > 0$ → функция возрастает.
2. В точке $x = -4$: производная меняется с + на − → локальный максимум.
3. На интервале $-4 < x < 3$: $f'(x) < 0$ → функция убывает.
4. В точке $x = 3$: производная меняется с − на + → локальный минимум.
5. На интервале $x > 3$: $f'(x) > 0$ → функция снова возрастает.

График:

б) Рис. 114

$$f^{\mathrm{\prime }}(x)>0\text{ при }0<x<2,f^{\mathrm{\prime }}(x)<0\text{ при }2<x<5,$$

$$f'(x) > 0 \text{ при } 0 < x < 2,\quad f'(x) < 0 \text{ при } 2 < x < 5,\quad f'(x) > 0 \text{ при } x > 5$$

Пошаговое рассуждение:

1. На интервале $0 < x < 2$: $f'(x) > 0$ → функция возрастает.
2. В точке $x = 2$: переход от + к − → локальный максимум.
3. На интервале $2 < x < 5$: $f'(x) < 0$ → функция убывает.
4. В точке $x = 5$: переход от − к + → локальный минимум.
5. На интервале $x > 5$: $f'(x) > 0$ → функция возрастает.

График:

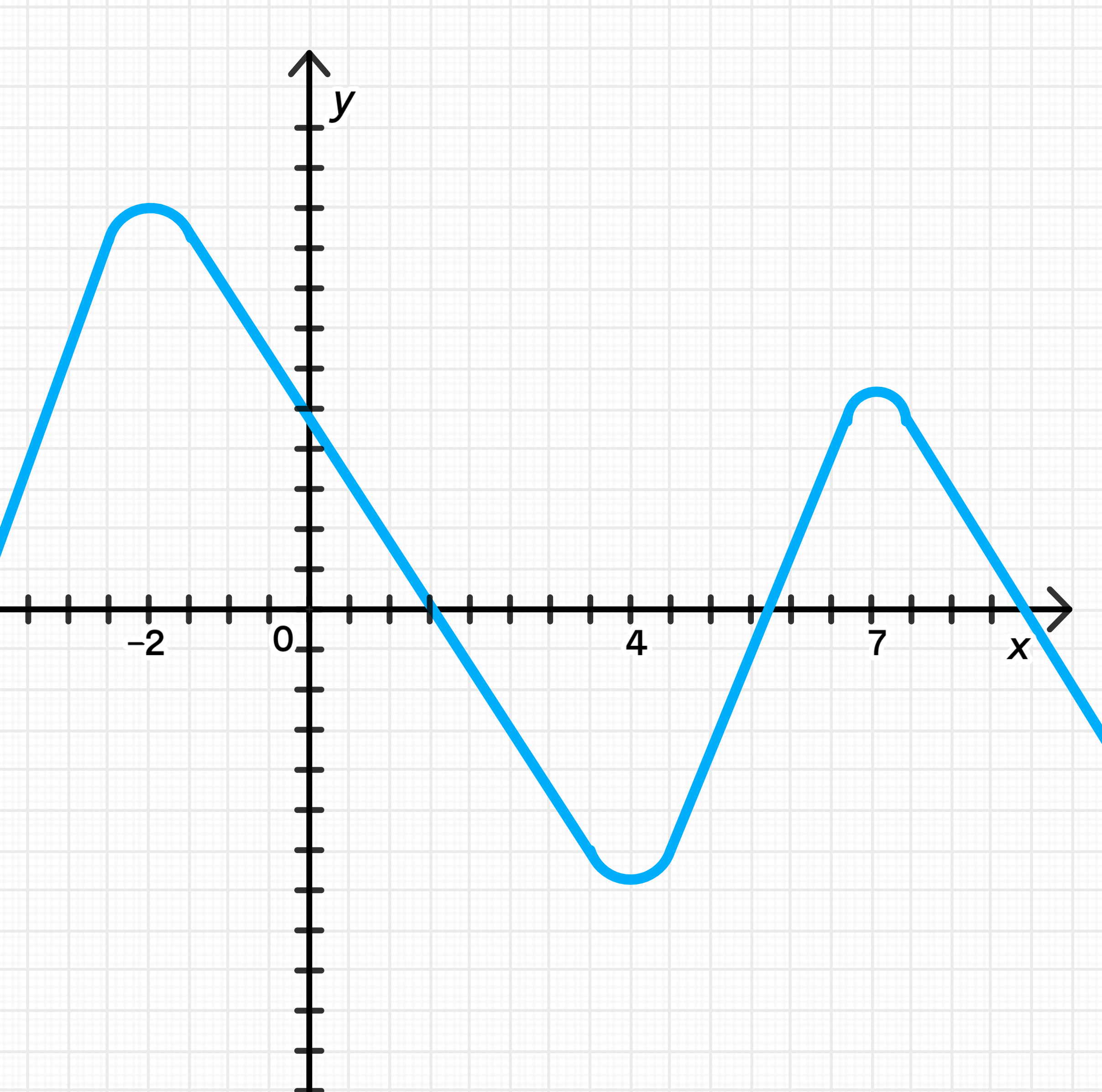
в) Рис. 115

$$f^{\mathrm{\prime }}(x)>0\text{ при }x<-2,f^{\mathrm{\prime }}(x)<0\text{ при }-2<x<4,$$

$$f'(x) > 0 \text{ при } x < -2,\quad f'(x) < 0 \text{ при } -2 < x < 4,\quad f'(x) > 0 \text{ при } 4 < x < 7,\quad f'(x) < 0 \text{ при } x > 7$$

Пошаговое рассуждение:

1. $x < -2$: $f'(x) > 0$ → функция возрастает.
2. $x = -2$: + на − → максимум.
3. $-2 < x < 4$: $f'(x) < 0$ → убывает.
4. $x = 4$: − на + → минимум.
5. $4 < x < 7$: $f'(x) > 0$ → возрастает.
6. $x = 7$: + на − → максимум.
7. $x > 7$: $f'(x) < 0$ → убывает.

График:

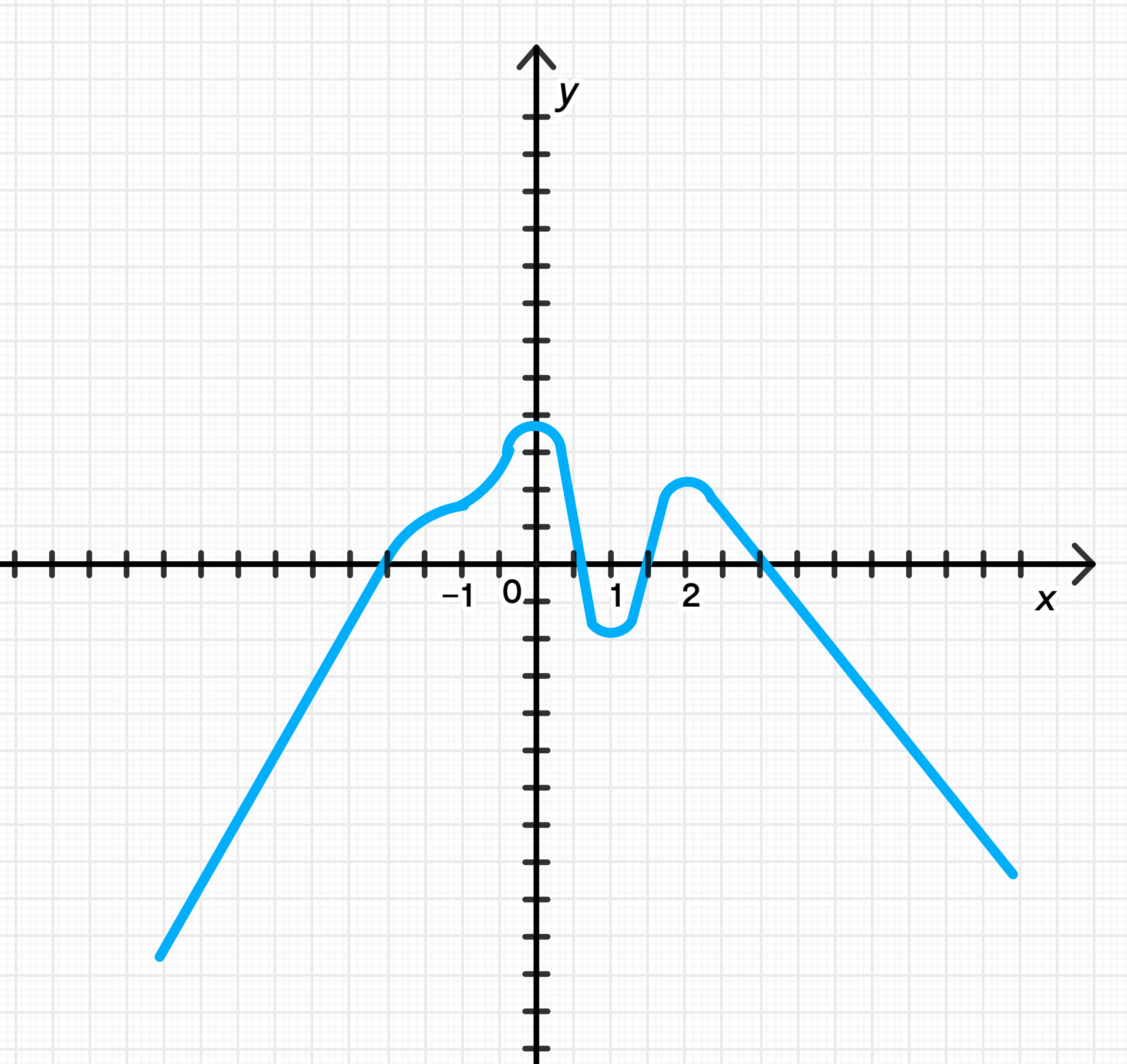
г) Рис. 116

$$f^{\mathrm{\prime }}(x)>0\text{ при }x<1,f^{\mathrm{\prime }}(x)<0\text{ при }1<x<2,$$

$$f'(x) > 0 \text{ при } x < 1,\quad f'(x) < 0 \text{ при } 1 < x < 2,\quad f'(x) > 0 \text{ при } 2 < x < 3,\quad f'(x) < 0 \text{ при } x > 3$$

Пошаговое рассуждение:

1. $x < 1$: $f'(x) > 0$ → возрастает.
2. $x = 1$: + на − → максимум.
3. $1 < x < 2$: $f'(x) < 0$ → убывает.
4. $x = 2$: − на + → минимум.
5. $2 < x < 3$: $f'(x) > 0$ → возрастает.
6. $x = 3$: + на − → максимум.
7. $x > 3$: $f'(x) < 0$ → убывает.

График: