ГДЗ по Алгебре 10 Класс Номер 45.11 Профильный Уровень Мордкович — Подробные Ответы

а) Постройте график функции $y = x^4 — 2x^2 + 3$.

б) При каких значениях параметра $a$ уравнение $x^4 — 2x^2 + 3 = a$ имеет три корня?

а) $f(x) = x^4 — 2x^2 + 3$;

$f'(x) = (x^4)’ — 2(x^2)’ + (3)’ = 4x^3 — 2 \cdot 2x + 0 = 4x^3 — 4x;$

Промежутки монотонности:

$$4x^3 — 4x \geq 0;$$ $$x^3 — x \geq 0;$$ $$x(x^2 — 1) \geq 0;$$ $$(x + 1) \cdot x \cdot (x — 1) \geq 0;$$ $$-1 \leq x \leq 0 \text{ или } x \geq 1;$$

Возрастает на $[-1; 0] \cup [1; +\infty)$ и убывает на $(-\infty; -1] \cup [0; 1]$;

Стационарные точки:

$$y_{\max} = f(0) = 0^4 — 2 \cdot 0^2 + 3 = 3;$$ $$y_{\min} = f(\pm 1) = (\pm 1)^4 — 2 \cdot (\pm 1)^2 + 3 = 1 — 2 + 3 = 2;$$

Координаты точек:

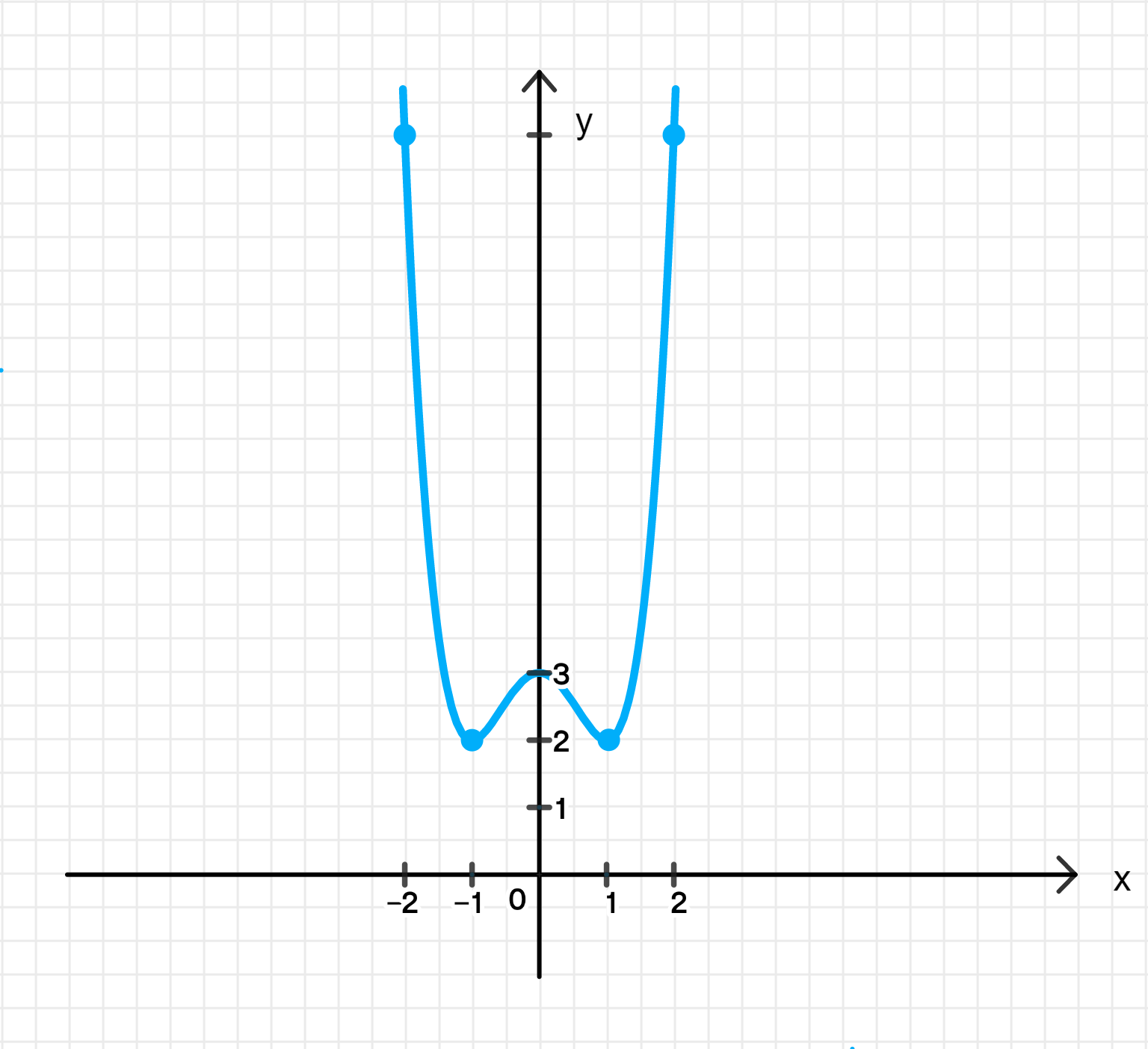
График функции:

б) Уравнение $x^4 — 2x^2 + 3 = a$ имеет три корня при $a \in (2; 3]$.

а) Построение графика функции $f(x) = x^4 — 2x^2 + 3$

Шаг 1: Нахождение производной функции

Для начала найдем первую производную функции $f(x) = x^4 — 2x^2 + 3$, чтобы затем определить её монотонность.

$$f'(x) = \frac{d}{dx}(x^4) — 2 \cdot \frac{d}{dx}(x^2) + \frac{d}{dx}(3)$$

Используя стандартные правила дифференцирования (для степенных функций $x^n$ производная равна $n \cdot x^{n-1}$):

$$f'(x) = 4x^3 — 4x$$

Шаг 2: Определение промежутков монотонности

Теперь, чтобы понять, на каких промежутках функция возрастает или убывает, нужно решить неравенство $f'(x) \geq 0$:

$$4x^3 — 4x \geq 0$$ $$4x(x^2 — 1) \geq 0$$

Разложим на множители:

$$4x(x — 1)(x + 1) \geq 0$$

Решим неравенство. Для этого выделим критические точки, которые задаются нулями множителей:

$$x = 0, \, x = 1, \, x = -1$$

Теперь определим знаки произведения на интервалах, определённых этими точками: $(-\infty, -1)$, $(-1, 0)$, $(0, 1)$, $(1, \infty)$.

1. Для $x \in (-\infty, -1)$: все множители отрицательные, следовательно, $f'(x) > 0$.
2. Для $x \in (-1, 0)$: $x$ отрицательное, $(x — 1)$ отрицательное, $(x + 1)$ положительное, следовательно, $f'(x) < 0$.
3. Для $x \in (0, 1)$: $x$ положительное, $(x — 1)$ отрицательное, $(x + 1)$ положительное, следовательно, $f'(x) < 0$.
4. Для $x \in (1, \infty)$: все множители положительные, следовательно, $f'(x) > 0$.

Таким образом, функция возрастает на интервалах $(-\infty, -1] \cup [1, +\infty)$ и убывает на интервалах $[-1, 0] \cup [0, 1]$.

Шаг 3: Стационарные точки и их классификация

Стационарные точки — это такие точки, в которых первая производная $f'(x) = 0$.

$$4x^3 — 4x = 0$$ $$4x(x^2 — 1) = 0$$ $$x = 0 \quad \text{или} \quad x = 1, -1$$

Теперь вычислим значения функции в этих точках:

1. $f(0) = 0^4 — 2 \cdot 0^2 + 3 = 3$
2. $f(1) = 1^4 — 2 \cdot 1^2 + 3 = 1 — 2 + 3 = 2$
3. $f(-1) = (-1)^4 — 2 \cdot (-1)^2 + 3 = 1 — 2 + 3 = 2$

Теперь классифицируем эти точки как максимумы или минимумы:

• В точке $x = 0$ функция достигает локального максимума, так как $f'(x)$ меняет знак с плюса на минус.
• В точках $x = \pm 1$ функция достигает локального минимума, так как $f'(x)$ меняет знак с минуса на плюс.

Таким образом:

• Максимум в точке $x = 0$, $f(0) = 3$.
• Минимум в точках $x = 1$ и $x = -1$, $f(1) = f(-1) = 2$.

Шаг 4: Координаты некоторых точек

Для более точного графика можно вычислить значения функции для других точек:

• $f(-2) = (-2)^4 — 2 \cdot (-2)^2 + 3 = 16 — 8 + 3 = 11$
• $f(2) = 2^4 — 2 \cdot 2^2 + 3 = 16 — 8 + 3 = 11$

Полученные точки для графика:

Шаг 5: График функции

б) Уравнение $x^4 — 2x^2 + 3 = a$ имеет три корня при $a \in (2; 3]$

Для того чтобы уравнение $x^4 — 2x^2 + 3 = a$ имело три корня, необходимо, чтобы функция $f(x) = x^4 — 2x^2 + 3$ пересекала горизонтальную прямую $y = a$ в трёх точках. Рассмотрим функции для различных значений $a$:

1. Если $a = 3$, то у нас будет ровно одна точка пересечения на оси $x$ в точке $x = 0$ (максимум функции).
2. Если $a \in (2; 3)$, то функция будет иметь два корня на интервале $(-\infty, 0)$ и один корень на интервале $(0, \infty)$, всего три корня.
3. Если $a = 2$, то у нас будет два корня в точках $x = \pm 1$ (минимумы функции).

Таким образом, уравнение $x^4 — 2x^2 + 3 = a$ имеет три корня, когда $a \in (2; 3]$.