ГДЗ по Алгебре 10 Класс Номер 45.12 Профильный Уровень Мордкович — Подробные Ответы

а) Постройте график функции $y = -x^4 + 2x^2 + 8$.

б) При каких значениях параметра $a$ уравнение $-x^4 + 2x^2 + 8 = a$ не имеет корней?

а) $f(x) = -x^4 + 2x^2 + 8$;

$f'(x) = -(x^4)’ + 2(x^2)’ + (8)’ = -4x^3 + 2 \cdot 2x + 0 = 4x — 4x^3$;

Промежутки монотонности:

$$4x — 4x^3 \geq 0;$$ $$x — x^3 \geq 0;$$ $$x(1 — x^2) \geq 0;$$ $$x(1 — x)(1 + x) \geq 0;$$ $$x \leq -1 \text{ или } 0 \leq x \leq 1;$$

Возрастает на $(-\infty; -1] \cup [0; 1]$ и убывает на $[-1; 0] \cup [1; +\infty)$.

Стационарные точки:

$$y_{\max} = f(\pm 1) = -( \pm 1)^4 + 2 \cdot (\pm 1)^2 + 8 = -1 + 2 + 8 = 9;$$ $$y_{\min} = f(0) = 0^4 — 2 \cdot 0^2 + 8 = 8$$

Координаты точек:

$$\begin{array}{|c|c|c|} \hline x & -2 & 2 \\ \hline y & 0 & 0 \\ \hline \end{array}$$

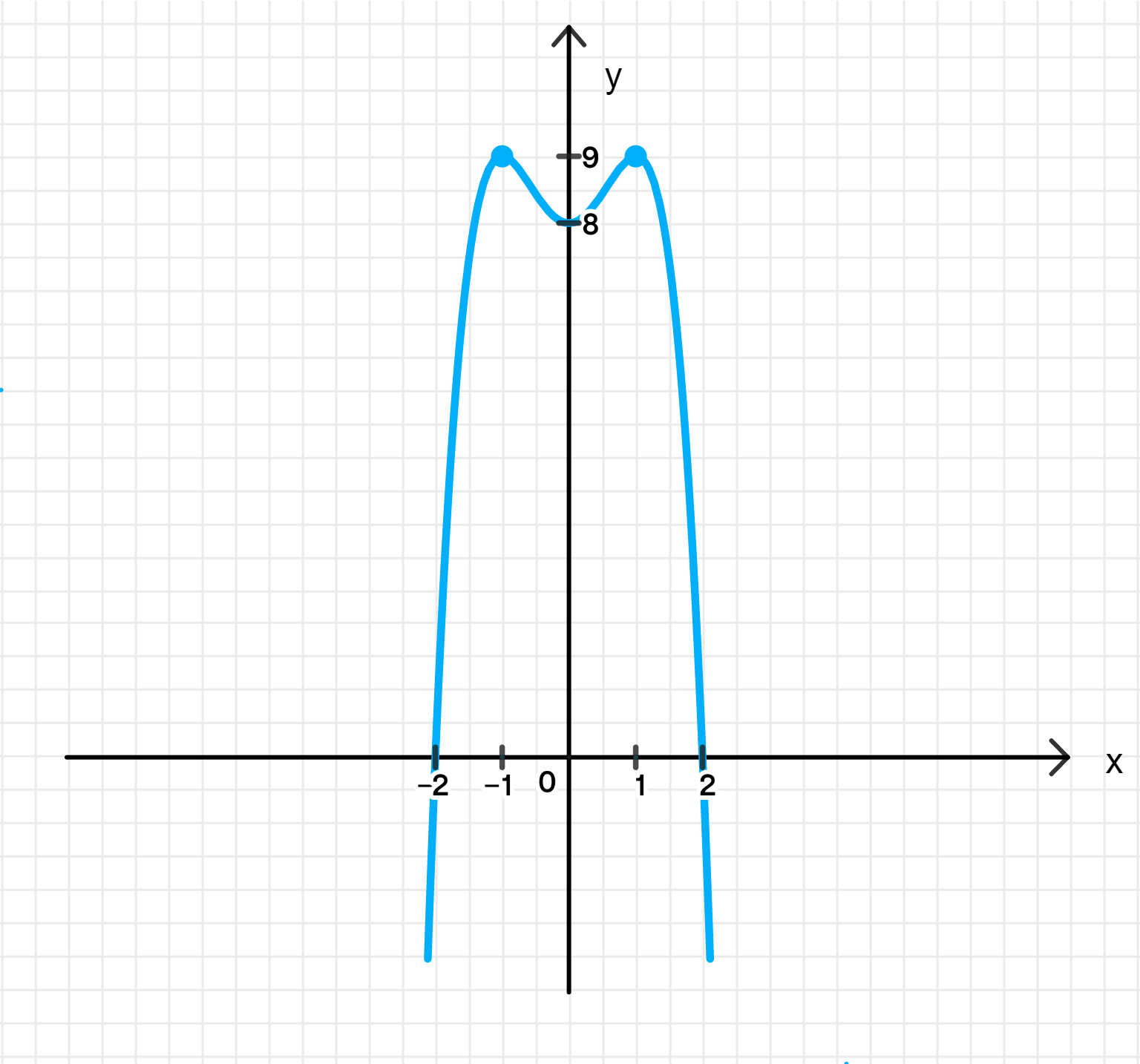
График функции:

б) Уравнение $-x^4 + 2x^2 + 8 = a$ не имеет корней при $a > 9$.

а) Построить график функции $f(x) = -x^4 + 2x^2 + 8$.

Для того чтобы построить график функции, нам необходимо:

1. Найти производную функции для определения промежутков монотонности и стационарных точек.
2. Определить промежутки возрастания и убывания функции.
3. Найти стационарные точки (максимумы и минимумы функции).
4. Построить таблицу значений функции.
5. Оценить поведение функции в особых точках (например, $x = 0, \pm 1$) и построить сам график.

1. Нахождение производной функции $f(x) = -x^4 + 2x^2 + 8$

Найдем производную функции, используя правила дифференцирования:

$$f'(x) = \frac{d}{dx}(-x^4 + 2x^2 + 8) = -4x^3 + 4x$$

Итак, производная функции:

$$f'(x) = -4x^3 + 4x = 4x(1 — x^2)$$

2. Определение промежутков монотонности

Теперь, чтобы найти промежутки возрастания и убывания функции, нужно решить неравенство $f'(x) \geq 0$.

$$f'(x) = 4x(1 — x^2)$$

Решим неравенство:

$$4x(1 — x^2) \geq 0$$

Перепишем неравенство:

$$x(1 — x^2) \geq 0$$

Разложим на множители:

$$x(1 — x)(1 + x) \geq 0$$

Решим полученное неравенство. Для этого найдем критические точки: $x = 0, -1, 1$. Эти точки делят числовую прямую на интервалы: $(-\infty; -1), (-1; 0), (0; 1), (1; +\infty)$.

Проверим знак выражения $x(1 — x)(1 + x)$ на каждом из интервалов:

• На интервале $(-\infty; -1)$: Все множители $x$, $1 — x$, и $1 + x$ отрицательны, значит, произведение положительное.
• На интервале $(-1; 0)$: Множитель $x$ отрицателен, $1 — x$ положителен, а $1 + x$ положителен, значит, произведение отрицательное.
• На интервале $(0; 1)$: Множитель $x$ положителен, $1 — x$ положителен, а $1 + x$ положителен, значит, произведение положительное.
• На интервале $(1; +\infty)$: Множитель $x$ положителен, $1 — x$ отрицателен, а $1 + x$ положителен, значит, произведение отрицательное.

Таким образом, неравенство выполняется на интервалах $(-\infty; -1] \cup [0; 1]$.

Функция возрастает на интервалах $(-\infty; -1] \cup [0; 1]$ и убывает на интервалах $[-1; 0] \cup [1; +\infty)$.

3. Определение стационарных точек

Стационарные точки — это точки, где производная равна нулю, то есть $f'(x) = 0$.

$$f'(x) = 4x(1 — x^2) = 0$$

Решение этого уравнения:

$$x = 0, \quad x = -1, \quad x = 1$$

Теперь подставим эти значения в исходную функцию $f(x) = -x^4 + 2x^2 + 8$, чтобы найти значения функции в этих точках:

• Для $x = 0$:

$$f(0) = -(0)^4 + 2 \cdot (0)^2 + 8 = 8$$

• Для $x = 1$:

$$f(1) = -(1)^4 + 2 \cdot (1)^2 + 8 = -1 + 2 + 8 = 9$$

• Для $x = -1$:

$$f(-1) = -(-1)^4 + 2 \cdot (-1)^2 + 8 = -1 + 2 + 8 = 9$$

Таким образом, стационарные точки: $(0, 8)$, $(1, 9)$, $(-1, 9)$.

Из этого видно, что на интервале $x \in [-1; 1]$ функция достигает максимума в точках $x = -1$ и $x = 1$ (значение $y = 9$) и минимума в точке $x = 0$ (значение $y = 8$).

4. Построение таблицы значений

Теперь составим таблицу значений функции на нескольких точках:

$$\begin{array}{|c|c|c|} \hline x & -2 & -1 & 0 & 1 & 2 \\ \hline f(x) & 0 & 9 & 8 & 9 & 0 \\ \hline \end{array}$$

5. Построение графика функции

б) Уравнение $-x^4 + 2x^2 + 8 = a$ не имеет корней при $a > 9$.

Чтобы найти значения $a$, при которых уравнение не имеет корней, нужно рассмотреть поведение функции. Видно, что на интервале $x \in [-1, 1]$ функция достигает максимума (значение $y = 9$) и минимума (значение $y = 8$) в точке $x = 0$.

Таким образом, уравнение $-x^4 + 2x^2 + 8 = a$ не имеет корней, если $a > 9$, поскольку в этом случае значение функции не может достичь значения $a$, а значит, решений уравнения не существует.