Краткий ответ:
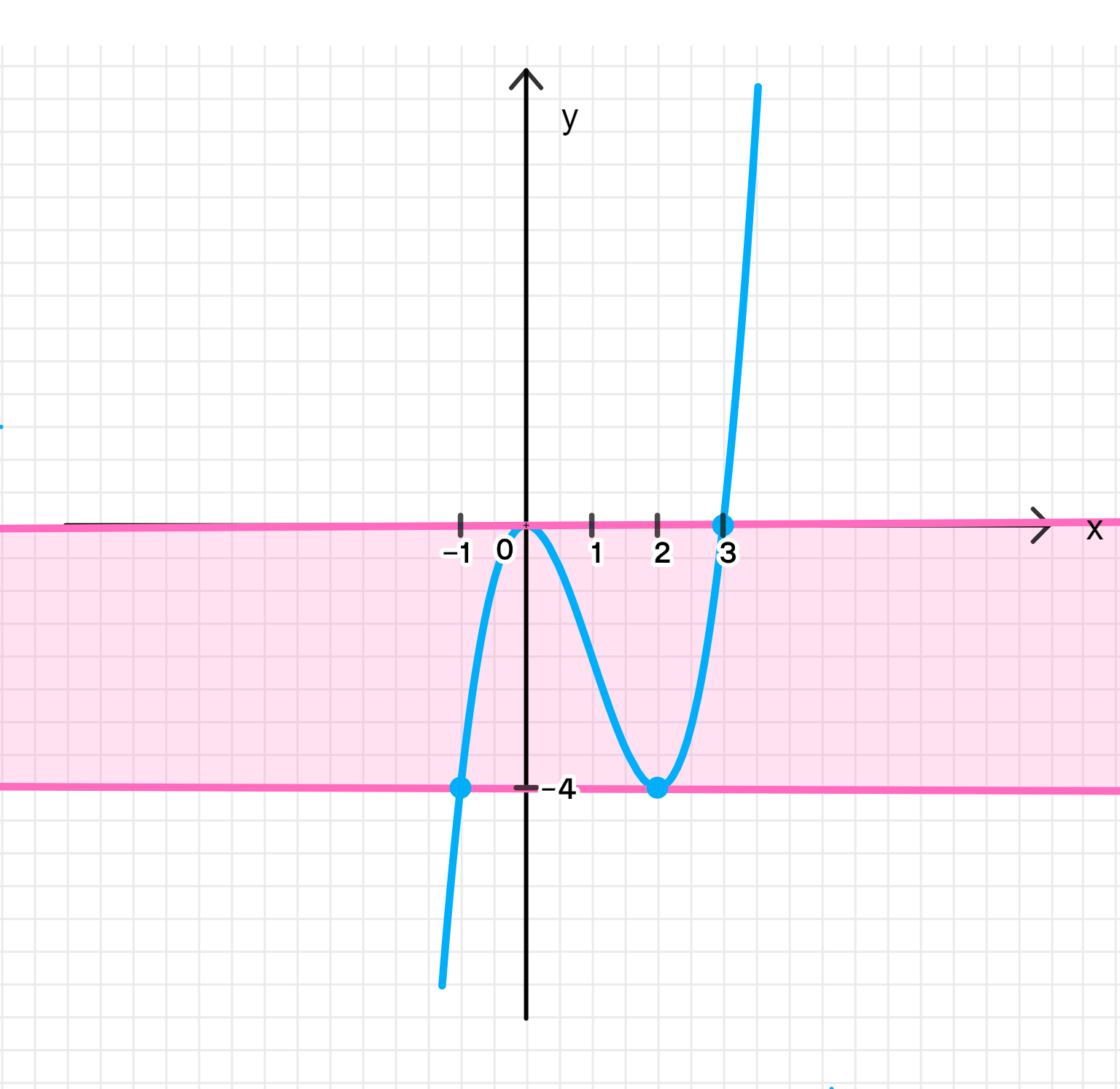
а) x 3 − 3 x 2 = a x^3 — 3x^2 = a − 4 < a < 0 -4 < a < 0
f ′ ( x ) = ( x 3 ) ′ − 3 ( x 2 ) ′ = 3 x 2 − 3 ⋅ 2 x = 3 x 2 − 6 x ; f'(x) = (x^3)’ — 3(x^2)’ = 3x^2 — 3 \cdot 2x = 3x^2 — 6x;
Промежутки монотонности:
3 x 2 − 6 x ≥ 0 ; 3x^2 — 6x \geq 0; 3 x ( x − 2 ) ≥ 0 ; 3x(x — 2) \geq 0; x ≤ 0 или x ≥ 2 ; x \leq 0 \text{ или } x \geq 2;
Возрастает на ( − ∞ ; 0 ] ∪ [ 2 ; + ∞ ) (-∞; 0] \cup [2; +∞) [ 0 ; 2 ] [0; 2]
Стационарные точки:
y m a x = f ( 0 ) = 0 3 − 3 ⋅ 0 2 = 0 ; y_{max} = f(0) = 0^3 — 3 \cdot 0^2 = 0; y m i n = f ( 2 ) = 2 3 − 3 ⋅ 2 2 = 8 − 3 ⋅ 4 = 8 − 12 = − 4 ; y_{min} = f(2) = 2^3 — 3 \cdot 2^2 = 8 — 3 \cdot 4 = 8 — 12 = -4;
Координаты точек:
x − 1 3 y − 4 0 \begin{array}{|c|c|c|} \hline x & -1 & 3 \\ \hline y & -4 & 0 \\ \hline \end{array}
График функции:
Ответ: 3 корня.
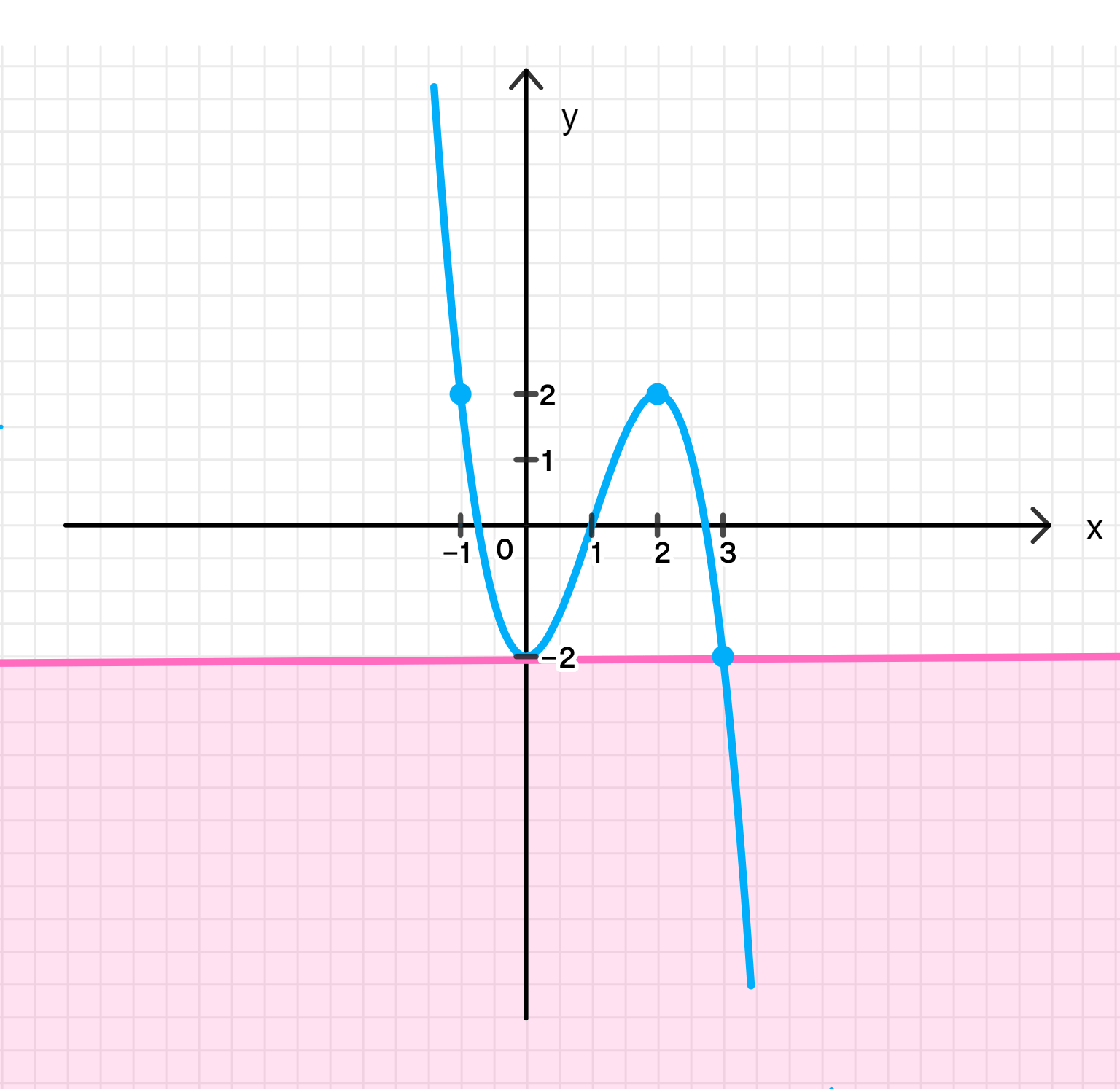
б) − x 3 + 3 x 2 − 2 = a -x^3 + 3x^2 — 2 = a a < − 2 a < -2
f ′ ( x ) = − ( x 3 ) ′ + 3 ( x 2 ) ′ − ( 2 ) ′ = − 3 x 2 + 3 ⋅ 2 x = 6 x − 3 x 2 ; f'(x) = -(x^3)’ + 3(x^2)’ — (2)’ = -3x^2 + 3 \cdot 2x = 6x — 3x^2;
Промежутки монотонности:
6 x − 3 x 2 ≥ 0 ; 6x — 3x^2 \geq 0; 3 x ( 2 − x ) ≥ 0 ; 3x(2 — x) \geq 0; 0 ≤ x ≤ 2 ; 0 \leq x \leq 2;
Возрастает на [ 0 ; 2 ] [0; 2] ( − ∞ ; 0 ] ∪ [ 2 ; + ∞ ) (-∞; 0] \cup [2; +∞)
Стационарные точки:
y m a x = f ( 2 ) = − 2 3 + 3 ⋅ 2 2 − 2 = − 8 + 3 ⋅ 4 − 2 = 12 − 10 = 2 ; y_{max} = f(2) = -2^3 + 3 \cdot 2^2 — 2 = -8 + 3 \cdot 4 — 2 = 12 — 10 = 2; y m i n = f ( 0 ) = − 0 3 + 3 ⋅ 0 2 − 2 = − 2 ; y_{min} = f(0) = -0^3 + 3 \cdot 0^2 — 2 = -2;
Координаты точек:
x − 1 3 y 2 − 2 \begin{array}{|c|c|c|} \hline x & -1 & 3 \\ \hline y & 2 & -2 \\ \hline \end{array}
График функции:
Ответ: 1 корень.
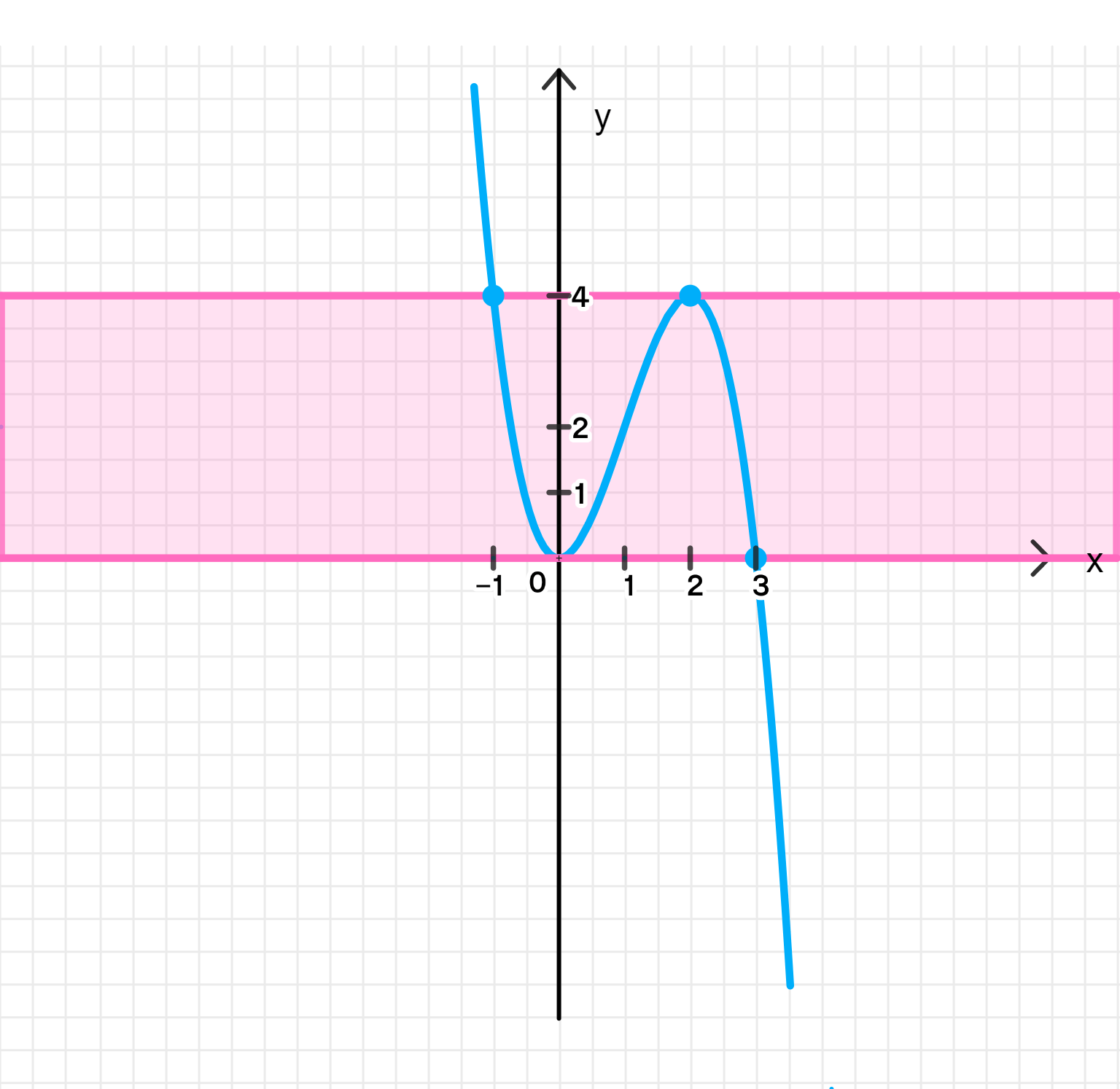
в) 3 x 2 − x 3 = a 3x^2 — x^3 = a 0 < a < 4 0 < a < 4
f ′ ( x ) = 3 ( x 2 ) ′ − ( x 3 ) ′ = 3 ⋅ 2 x − 3 x 2 = 6 x − 3 x 2 ; f'(x) = 3(x^2)’ — (x^3)’ = 3 \cdot 2x — 3x^2 = 6x — 3x^2;
Промежутки монотонности:
6 x − 3 x 2 ≥ 0 ; 6x — 3x^2 \geq 0; 3 x ( 2 − x ) ≥ 0 ; 3x(2 — x) \geq 0; 0 ≤ x ≤ 2 ; 0 \leq x \leq 2;
Возрастает на [ 0 ; 2 ] [0; 2] ( − ∞ ; 0 ] ∪ [ 2 ; + ∞ ) (-∞; 0] \cup [2; +∞)
Стационарные точки:
y m a x = f ( 2 ) = 3 ⋅ 2 2 − 2 3 = 3 ⋅ 4 − 8 = 12 − 8 = 4 ; y_{max} = f(2) = 3 \cdot 2^2 — 2^3 = 3 \cdot 4 — 8 = 12 — 8 = 4; y m i n = f ( 0 ) = 3 ⋅ 0 2 − 0 3 = 0 ; y_{min} = f(0) = 3 \cdot 0^2 — 0^3 = 0;
Координаты точек:
x − 1 3 y 4 0 \begin{array}{|c|c|c|} \hline x & -1 & 3 \\ \hline y & 4 & 0 \\ \hline \end{array}
График функции:
Ответ: 3 корня.
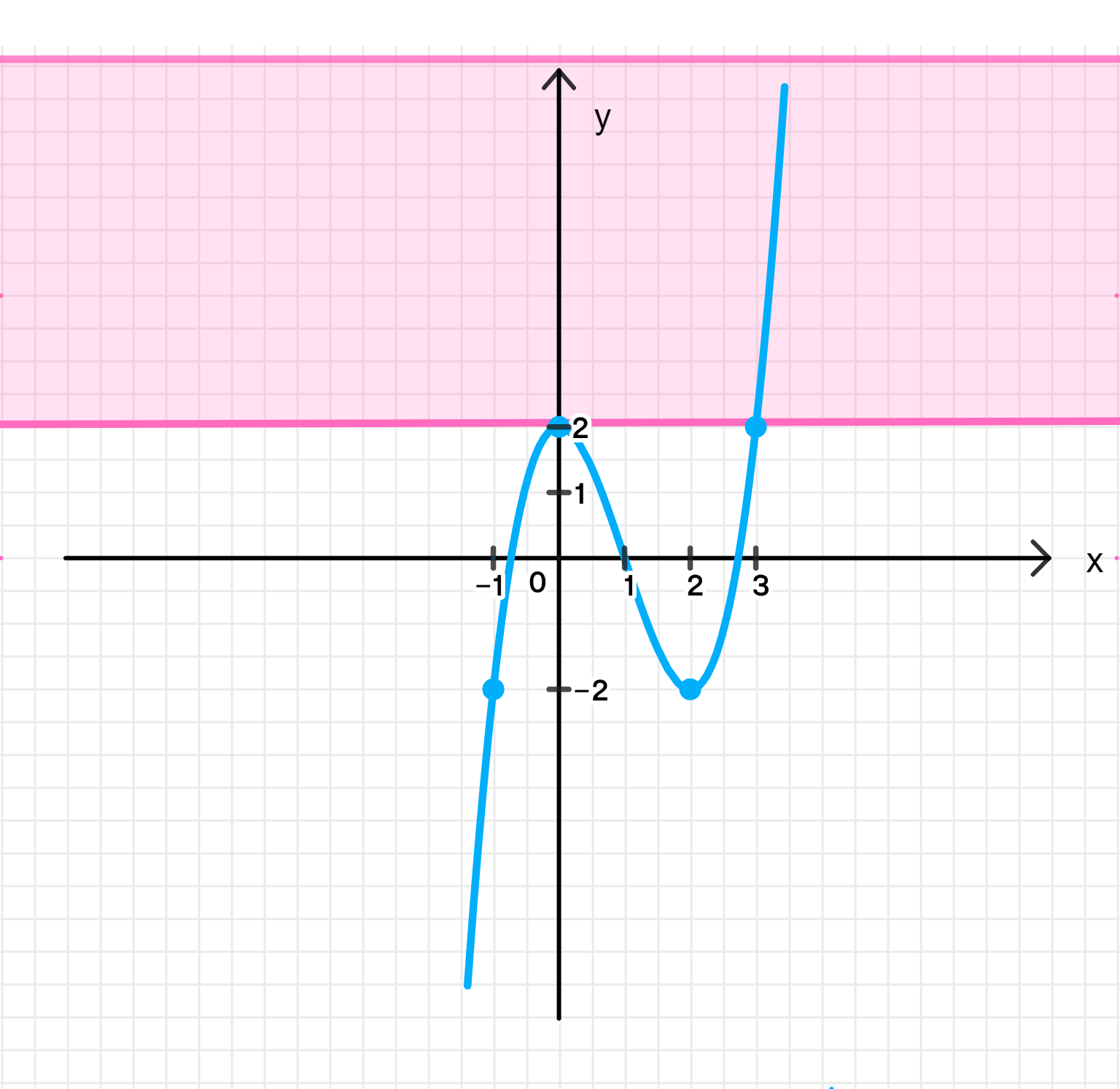
г) x 3 − 3 x 2 + 2 = a x^3 — 3x^2 + 2 = a a > 2 a > 2
f ′ ( x ) = ( x 3 ) ′ − 3 ( x 2 ) ′ + ( 2 ) ′ = 3 x 2 − 3 ⋅ 2 x + 0 = 3 x 2 − 6 x ; f'(x) = (x^3)’ — 3(x^2)’ + (2)’ = 3x^2 — 3 \cdot 2x + 0 = 3x^2 — 6x;
Промежутки монотонности:
3 x 2 − 6 x ≥ 0 ; 3x^2 — 6x \geq 0; 3 x ( x − 2 ) ≥ 0 ; 3x(x — 2) \geq 0; x ≤ 0 или x ≥ 2 ; x \leq 0 \text{ или } x \geq 2;
Возрастает на ( − ∞ ; 0 ] ∪ [ 2 ; + ∞ ) (-∞; 0] \cup [2; +∞) [ 0 ; 2 ] [0; 2]
Стационарные точки:
y m a x = f ( 0 ) = 0 3 − 3 ⋅ 0 2 + 2 = 2 ; y_{max} = f(0) = 0^3 — 3 \cdot 0^2 + 2 = 2; y m i n = f ( 2 ) = 2 3 − 3 ⋅ 2 2 + 2 = 8 − 3 ⋅ 4 + 2 = 10 − 12 = − 2 ; y_{min} = f(2) = 2^3 — 3 \cdot 2^2 + 2 = 8 — 3 \cdot 4 + 2 = 10 — 12 = -2;
Координаты точек:
x − 1 3 y − 4 0 \begin{array}{|c|c|c|} \hline x & -1 & 3 \\ \hline y & -4 & 0 \\ \hline \end{array}
График функции:
Ответ: 1 корень.
Подробный ответ:
а) x 3 − 3 x 2 = a x^3 — 3x^2 = a − 4 < a < 0 -4 < a < 0
Шаг 1: Нахождение производной функции
Найдем производную функции f ( x ) = x 3 − 3 x 2 f(x) = x^3 — 3x^2
f ′ ( x ) = ( x 3 ) ′ − 3 ( x 2 ) ′ = 3 x 2 − 6 x . f'(x) = (x^3)’ — 3(x^2)’ = 3x^2 — 6x.
Шаг 2: Промежутки монотонности
Для нахождения промежутков монотонности решим неравенство f ′ ( x ) ≥ 0 f'(x) \geq 0
3 x 2 − 6 x ≥ 0 ⇒ 3 x ( x − 2 ) ≥ 0. 3x^2 — 6x \geq 0 \quad \Rightarrow \quad 3x(x — 2) \geq 0.
Корни этого неравенства: x = 0 x = 0 x = 2 x = 2
Рассмотрим знаки на промежутках:
На промежутке ( − ∞ , 0 ) (-\infty, 0) На промежутке ( 0 , 2 ) (0, 2) На промежутке ( 2 , + ∞ ) (2, +\infty) Таким образом:
Функция возрастает на ( − ∞ ; 0 ] ∪ [ 2 ; + ∞ ) (-\infty; 0] \cup [2; +\infty) Функция убывает на [ 0 ; 2 ] [0; 2] Шаг 3: Стационарные точки
Для нахождения стационарных точек подставим значения x = 0 x = 0 x = 2 x = 2 f ( x ) = x 3 − 3 x 2 f(x) = x^3 — 3x^2
f ( 0 ) = 0 3 − 3 ⋅ 0 2 = 0 f(0) = 0^3 — 3 \cdot 0^2 = 0 f ( 2 ) = 2 3 − 3 ⋅ 2 2 = 8 − 12 = − 4 f(2) = 2^3 — 3 \cdot 2^2 = 8 — 12 = -4 Итак, мы имеем:
Максимум f ( 0 ) = 0 f(0) = 0 Минимум f ( 2 ) = − 4 f(2) = -4 Шаг 4: Координаты точек
Заданы значения x = − 1 x = -1 x = 3 x = 3
f ( − 1 ) = ( − 1 ) 3 − 3 ( − 1 ) 2 = − 1 − 3 = − 4 f(-1) = (-1)^3 — 3(-1)^2 = -1 — 3 = -4 f ( 3 ) = 3 3 − 3 ⋅ 3 2 = 27 − 27 = 0 f(3) = 3^3 — 3 \cdot 3^2 = 27 — 27 = 0 Таким образом, координаты точек:
x − 1 3 y − 4 0 \begin{array}{|c|c|c|} \hline x & -1 & 3 \\ \hline y & -4 & 0 \\ \hline \end{array}
Шаг 5: График функции
Ответ: 3 корня.
б) − x 3 + 3 x 2 − 2 = a -x^3 + 3x^2 — 2 = a a < − 2 a < -2
Шаг 1: Нахождение производной функции
Найдем производную функции f ( x ) = − x 3 + 3 x 2 − 2 f(x) = -x^3 + 3x^2 — 2
f ′ ( x ) = − ( x 3 ) ′ + 3 ( x 2 ) ′ − ( 2 ) ′ = − 3 x 2 + 6 x = 6 x − 3 x 2 . f'(x) = -(x^3)’ + 3(x^2)’ — (2)’ = -3x^2 + 6x = 6x — 3x^2.
Шаг 2: Промежутки монотонности
Решим неравенство f ′ ( x ) ≥ 0 f'(x) \geq 0
6 x − 3 x 2 ≥ 0 ⇒ 3 x ( 2 − x ) ≥ 0. 6x — 3x^2 \geq 0 \quad \Rightarrow \quad 3x(2 — x) \geq 0.
Корни этого неравенства: x = 0 x = 0 x = 2 x = 2
Рассмотрим знаки на промежутках:
На промежутке ( − ∞ , 0 ) (-\infty, 0) На промежутке ( 0 , 2 ) (0, 2) На промежутке ( 2 , + ∞ ) (2, +\infty) Таким образом:
Функция возрастает на [ 0 ; 2 ] [0; 2] Функция убывает на ( − ∞ ; 0 ] ∪ [ 2 ; + ∞ ) (-\infty; 0] \cup [2; +\infty) Шаг 3: Стационарные точки
Подставим значения x = 0 x = 0 x = 2 x = 2 f ( x ) = − x 3 + 3 x 2 − 2 f(x) = -x^3 + 3x^2 — 2
f ( 0 ) = − 0 3 + 3 ⋅ 0 2 − 2 = − 2 f(0) = -0^3 + 3 \cdot 0^2 — 2 = -2 f ( 2 ) = − 2 3 + 3 ⋅ 2 2 − 2 = − 8 + 12 − 2 = 2 f(2) = -2^3 + 3 \cdot 2^2 — 2 = -8 + 12 — 2 = 2 Итак, мы имеем:
Максимум f ( 2 ) = 2 f(2) = 2 Минимум f ( 0 ) = − 2 f(0) = -2 Шаг 4: Координаты точек
Заданы значения x = − 1 x = -1 x = 3 x = 3
f ( − 1 ) = − ( − 1 ) 3 + 3 ( − 1 ) 2 − 2 = 1 + 3 − 2 = 2 f(-1) = -(-1)^3 + 3(-1)^2 — 2 = 1 + 3 — 2 = 2 f ( 3 ) = − ( 3 ) 3 + 3 ⋅ 3 2 − 2 = − 27 + 27 − 2 = − 2 f(3) = -(3)^3 + 3 \cdot 3^2 — 2 = -27 + 27 — 2 = -2 Таким образом, координаты точек:
x − 1 3 y 2 − 2 \begin{array}{|c|c|c|} \hline x & -1 & 3 \\ \hline y & 2 & -2 \\ \hline \end{array}
Шаг 5: График функции
Ответ: 1 корень.
в) 3 x 2 − x 3 = a 3x^2 — x^3 = a 0 < a < 4 0 < a < 4
Шаг 1: Нахождение производной функции
Найдем производную функции f ( x ) = 3 x 2 − x 3 f(x) = 3x^2 — x^3
f ′ ( x ) = 3 ⋅ 2 x − 3 x 2 = 6 x − 3 x 2 . f'(x) = 3 \cdot 2x — 3x^2 = 6x — 3x^2.
Шаг 2: Промежутки монотонности
Решим неравенство f ′ ( x ) ≥ 0 f'(x) \geq 0
6 x − 3 x 2 ≥ 0 ⇒ 3 x ( 2 − x ) ≥ 0. 6x — 3x^2 \geq 0 \quad \Rightarrow \quad 3x(2 — x) \geq 0.
Корни этого неравенства: x = 0 x = 0 x = 2 x = 2
Рассмотрим знаки на промежутках:
На промежутке ( − ∞ , 0 ) (-\infty, 0) На промежутке ( 0 , 2 ) (0, 2) На промежутке ( 2 , + ∞ ) (2, +\infty) Таким образом:
Функция возрастает на [ 0 ; 2 ] [0; 2] Функция убывает на ( − ∞ ; 0 ] ∪ [ 2 ; + ∞ ) (-\infty; 0] \cup [2; +\infty) Шаг 3: Стационарные точки
Подставим значения x = 0 x = 0 x = 2 x = 2 f ( x ) = 3 x 2 − x 3 f(x) = 3x^2 — x^3
f ( 0 ) = 3 ⋅ 0 2 − 0 3 = 0 f(0) = 3 \cdot 0^2 — 0^3 = 0 f ( 2 ) = 3 ⋅ 2 2 − 2 3 = 12 − 8 = 4 f(2) = 3 \cdot 2^2 — 2^3 = 12 — 8 = 4 Итак, мы имеем:
Максимум f ( 2 ) = 4 f(2) = 4 Минимум f ( 0 ) = 0 f(0) = 0 Шаг 4: Координаты точек
Заданы значения x = − 1 x = -1 x = 3 x = 3
f ( − 1 ) = 3 ⋅ ( − 1 ) 2 − ( − 1 ) 3 = 3 + 1 = 4 f(-1) = 3 \cdot (-1)^2 — (-1)^3 = 3 + 1 = 4 f ( 3 ) = 3 ⋅ 3 2 − 3 3 = 27 − 27 = 0 f(3) = 3 \cdot 3^2 — 3^3 = 27 — 27 = 0 Таким образом, координаты точек:
x − 1 3 y 4 0 \begin{array}{|c|c|c|} \hline x & -1 & 3 \\ \hline y & 4 & 0 \\ \hline \end{array}
Шаг 5: График функции
Ответ: 3 корня.
г) x 3 − 3 x 2 + 2 = a x^3 — 3x^2 + 2 = a a > 2 a > 2
Шаг 1: Нахождение производной функции
Найдем производную функции f ( x ) = x 3 − 3 x 2 + 2 f(x) = x^3 — 3x^2 + 2
f ′ ( x ) = ( x 3 ) ′ − 3 ( x 2 ) ′ + ( 2 ) ′ = 3 x 2 − 6 x . f'(x) = (x^3)’ — 3(x^2)’ + (2)’ = 3x^2 — 6x.
Шаг 2: Промежутки монотонности
Решим неравенство f ′ ( x ) ≥ 0 f'(x) \geq 0
3 x 2 − 6 x ≥ 0 ⇒ 3 x ( x − 2 ) ≥ 0. 3x^2 — 6x \geq 0 \quad \Rightarrow \quad 3x(x — 2) \geq 0.
Корни этого неравенства: x = 0 x = 0 x = 2 x = 2
Рассмотрим знаки на промежутках:
На промежутке ( − ∞ , 0 ) (-\infty, 0) На промежутке ( 0 , 2 ) (0, 2) На промежутке ( 2 , + ∞ ) (2, +\infty) Таким образом:
Функция возрастает на ( − ∞ ; 0 ] ∪ [ 2 ; + ∞ ) (-\infty; 0] \cup [2; +\infty) Функция убывает на [ 0 ; 2 ] [0; 2] Шаг 3: Стационарные точки
Подставим значения x = 0 x = 0 x = 2 x = 2 f ( x ) = x 3 − 3 x 2 + 2 f(x) = x^3 — 3x^2 + 2
f ( 0 ) = 0 3 − 3 ⋅ 0 2 + 2 = 2 f(0) = 0^3 — 3 \cdot 0^2 + 2 = 2 f ( 2 ) = 2 3 − 3 ⋅ 2 2 + 2 = 8 − 12 + 2 = − 2 f(2) = 2^3 — 3 \cdot 2^2 + 2 = 8 — 12 + 2 = -2 Итак, мы имеем:
Максимум f ( 0 ) = 2 f(0) = 2 Минимум f ( 2 ) = − 2 f(2) = -2 Шаг 4: Координаты точек
Заданы значения x = − 1 x = -1 x = 3 x = 3
f ( − 1 ) = ( − 1 ) 3 − 3 ( − 1 ) 2 + 2 = − 1 − 3 + 2 = − 2 f(-1) = (-1)^3 — 3(-1)^2 + 2 = -1 — 3 + 2 = -2 f ( 3 ) = 3 3 − 3 ⋅ 3 2 + 2 = 27 − 27 + 2 = 2 f(3) = 3^3 — 3 \cdot 3^2 + 2 = 27 — 27 + 2 = 2 Таким образом, координаты точек:
x − 1 3 y − 4 0 \begin{array}{|c|c|c|} \hline x & -1 & 3 \\ \hline y & -4 & 0 \\ \hline \end{array}
Шаг 5: График функции
Ответ: 1 корень.