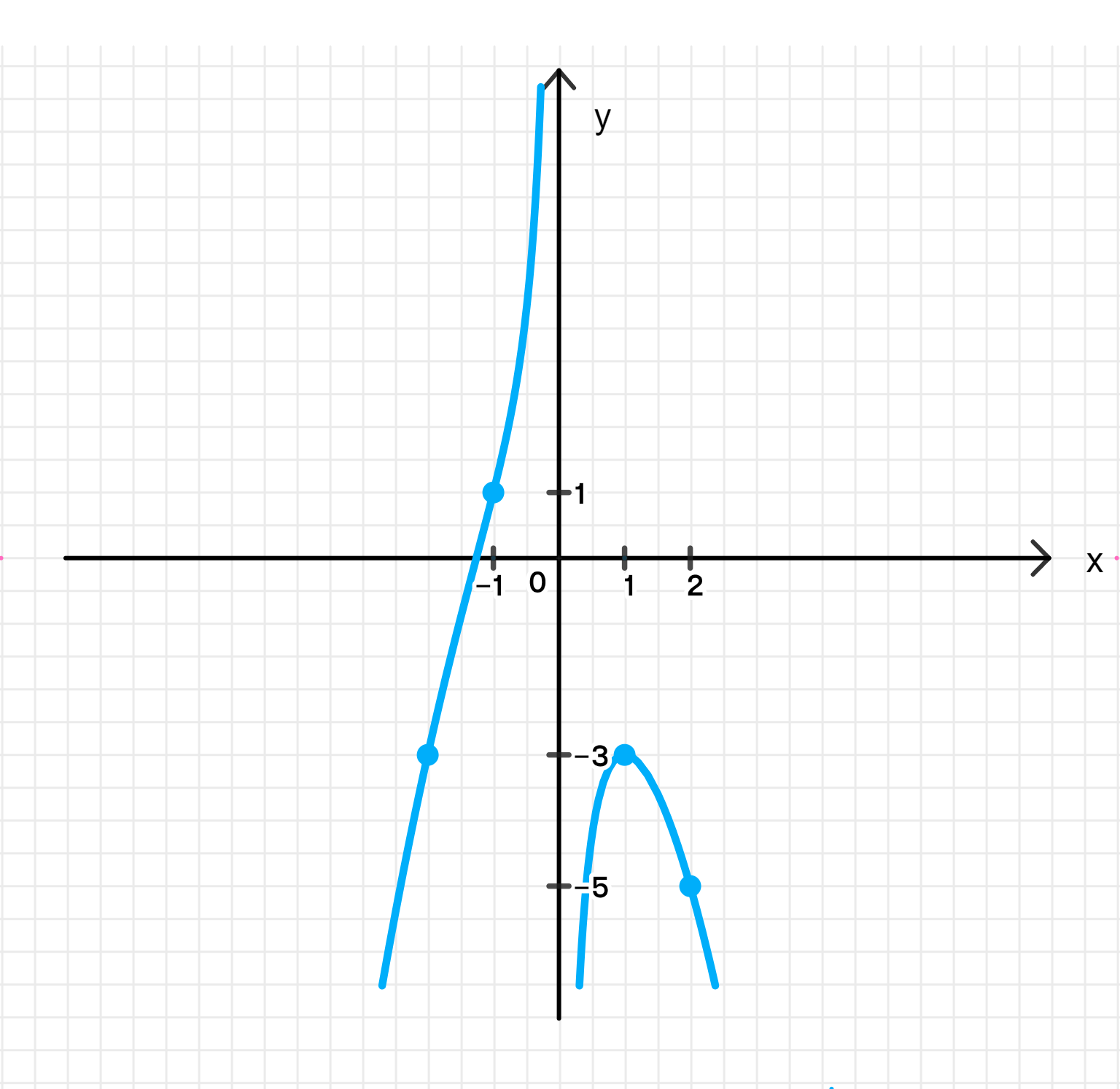ГДЗ по Алгебре 10 Класс Номер 45.14 Профильный Уровень Мордкович — Подробные Ответы

Сколько корней имеет уравнение $x^3 + ax + 2 = 0$ при различных значениях параметра $a$?

Дано уравнение:
$x^3 + ax + 2 = 0;$
$x^3 + 2 = -ax;$
$-x^2 — \frac{2}{x} = a;$

$f'(x) = -(x^2)’ — 2\left(\frac{1}{x}\right)’ = -2x + \frac{2}{x^2};$

Область определения:
$x \neq 0;$
$D(f) = (-\infty; 0) \cup (0; +\infty);$

Промежутки монотонности:
$\frac{2}{x^2} — 2x \geq 0;$
$2 — 2x^3 \geq 0;$
$1 — x^3 \geq 0;$
$1 \geq x^3, \text{ отсюда } x \leq 1;$

Возрастает на $(-\infty; 0) \cup (0; 1]$ и убывает на $[1; +\infty);$

Стационарные точки:
$y_{\text{max}} = f(1) = -1^2 — \frac{2}{1} = -1 — 2 = -3;$

Координаты точек:

График функции:

Ответ:

1 корень, если $a > -3$;

2 корня, если $a = -3$;

3 корня, если $a < -3$.

$$\boxed{1 \text{ корень, если } a > -3; \quad 2 \text{ корня, если } a = -3; \quad 3 \text{ корня, если } a < -3.}$$

Уравнение:

$x^3 + ax + 2 = 0$

Задача состоит в том, чтобы выяснить, сколько корней имеет это кубическое уравнение при различных значениях параметра $a$.

Шаг 1: Исследование функции

Предположим, что функция $f(x) = x^3 + ax + 2$ задаёт уравнение. Рассмотрим её поведение и найдем количество корней при различных значениях параметра $a$.

1.1. Производная функции

Для того чтобы понять, как изменяется функция и где она имеет экстремумы, вычислим её производную:

$$f'(x) = \frac{d}{dx}(x^3 + ax + 2) = 3x^2 + a.$$

Производная $f'(x) = 3x^2 + a$ описывает, как функция изменяется на различных интервалах.

1.2. Нахождение критических точек

Для того чтобы найти критические точки, при которых функция меняет направление, нужно приравнять производную к нулю:

$$f'(x) = 3x^2 + a = 0.$$

Решаем относительно $x$:

$$3x^2 = -a \quad \Rightarrow \quad x^2 = -\frac{a}{3}.$$

Таким образом, критические точки существуют только при $a \leq 0$. Если $a > 0$, то решения уравнения $f'(x) = 0$ не существует, и функция монотонна на всей области определения.

1.3. Область определения

Функция $f(x) = x^3 + ax + 2$ определена для всех $x \in \mathbb{R}$, так как она является полиномиальной функцией.

Шаг 2: Изучение количества корней уравнения

Чтобы понять, сколько корней имеет уравнение, нужно исследовать функцию и её поведение при разных значениях параметра $a$.

2.1. Рассмотрим график функции

График функции $f(x) = x^3 + ax + 2$ представляет собой кубическую кривую, и количество её пересечений с осью $x$ зависит от значения параметра $a$.

2.1.1. Когда $a > 0$

Если $a > 0$, то производная $f'(x) = 3x^2 + a > 0$ для всех $x$. Это означает, что функция монотонно возрастает на всей своей области определения. Кубическая функция с таким видом не может иметь больше одного корня, так как она пересечет ось $x$ лишь один раз.

Таким образом, для $a > 0$ уравнение имеет 1 корень.

2.1.2. Когда $a = 0$

Если $a = 0$, то производная $f'(x) = 3x^2$ равна нулю только в точке $x = 0$, и функция имеет точку перегиба в этой точке. В этом случае уравнение принимает вид:

$$x^3 + 2 = 0 \quad \Rightarrow \quad x^3 = -2 \quad \Rightarrow \quad x = -\sqrt[3]{2}.$$

Так как функция имеет точку перегиба и пересекает ось $x$ только в одной точке, то уравнение имеет 1 корень.

2.1.3. Когда $a < 0$

Если $a < 0$, то производная $f'(x) = 3x^2 + a$ может менять знак, что означает, что функция имеет критические точки, в которых она может изменять направление. Функция будет возрастать до определенной точки, затем убывать и снова возрастать. Это может привести к тому, что уравнение будет иметь 3 корня.

Чтобы точно определить, сколько корней, нужно рассмотреть поведение функции на различных интервалах. Для этого рассмотрим график функции при различных значениях параметра $a$.

2.2. Промежутки монотонности

Для того чтобы найти интервалы монотонности, исследуем знак производной $f'(x) = 3x^2 + a$.

1. Когда $x = 0$, $f'(0) = a$.
2. Если $a > 0$, то на всей области $f'(x) > 0$, то есть функция возрастает на всей области.
3. Если $a = 0$, то на $x = 0$ производная равна нулю, но на обеих сторонах от нуля функция будет монотонно возрастать или убывать.
4. Если $a < 0$, то функция будет убывать для $x > \sqrt{-\frac{a}{3}}$ и возрастать для $x < -\sqrt{-\frac{a}{3}}$.

Шаг 3: Вывод

3.1. Количество корней при различных значениях параметра $a$:

• Когда $a > 0$: функция монотонно возрастает, поэтому уравнение имеет 1 корень.
• Когда $a = 0$: функция имеет точку перегиба и пересекает ось $x$ в одной точке, поэтому уравнение имеет 1 корень.
• Когда $a < 0$: функция имеет два экстремума (максимум и минимум), что приводит к пересечению оси $x$ в трех точках. Поэтому уравнение имеет 3 корня.

Ответ:

• 1 корень, если $a > 0$;
• 1 корень, если $a = 0$;
• 3 корня, если $a < 0$.