ГДЗ по Алгебре 10 Класс Номер 45.16 Профильный Уровень Мордкович — Подробные Ответы

Решите уравнение:

$$\sqrt{x}(4x^3+3x^2-6x+2,75-\sin \pi x)=0$$

$$\sqrt{x}(4x^3 + 3x^2 — 6x + 2,75 — \sin \pi x) = 0;$$ $$\sqrt{x} = 0, \text{ отсюда } x = 0;$$ $$4x^3 + 3x^2 — 6x + 2,75 — \sin \pi x = 0;$$ $$4x^3 + 3x^2 — 6x = \sin \pi x — 2,75;$$

Область определения функции:

$$x \geq 0, \text{ значит } D(x) = [0; +\infty);$$

Левая часть уравнения:

$$f'(x) = (x^3)’ + 3(x^2)’ — (6x)’;$$ $$f'(x) = 4 \cdot 3x^2 + 3 \cdot 2x — 6 = 12x^2 + 6x — 6;$$

Промежутки монотонности:

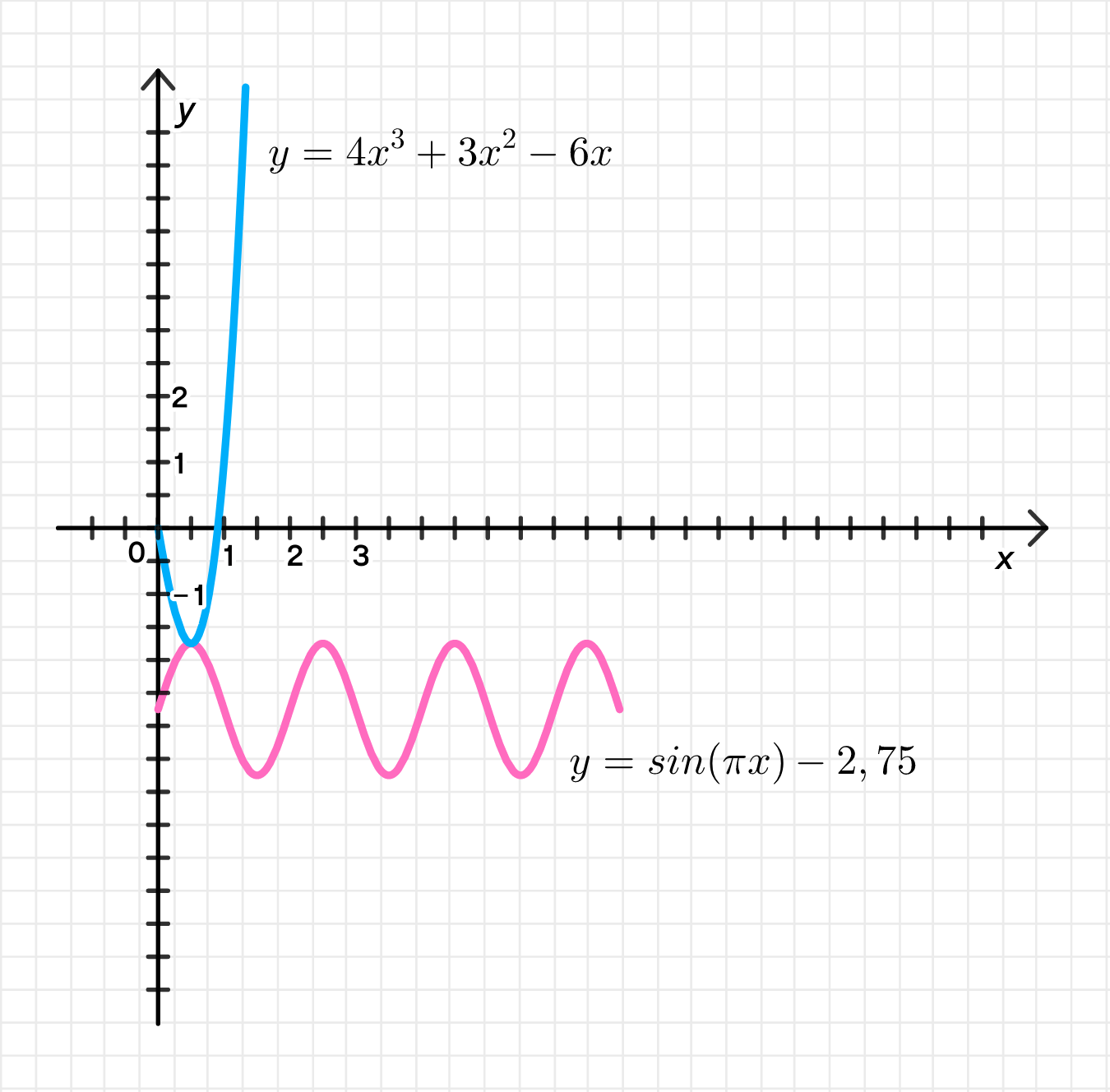
$$12x^2 + 6x — 6 \geq 0;$$ $$2x^2 + x — 1 \geq 0;$$ $$(2x — 1)(x + 1) \geq 0;$$ $$x \leq -1 \text{ или } x \geq \frac{1}{2};$$ $$\text{Возрастает на } [0,5; +\infty) \text{ и убывает на } [0; 0,5];$$

Стационарные точки:

$$y_{\text{min}} = f\left(\frac{1}{2}\right) = 4 \cdot \frac{1}{8} + 3 \cdot \frac{1}{4} — 6 \cdot \frac{1}{2} = \frac{4 + 6 — 24}{8} = -\frac{14}{8} = -1 \frac{3}{4};$$

Координаты точек:

Правая часть уравнения:

$$f'(x) = (\sin \pi x)’ — (2,75)’ = \pi \cos \pi x;$$

Промежутки монотонности:

$$\pi \cos \pi x \geq 0;$$ $$\cos \pi x \geq 0;$$ $$-\frac{\pi}{2} + 2\pi n \leq \pi x \leq \frac{\pi}{2} + 2\pi n;$$ $$-\frac{1}{2} + 2n \leq x \leq \frac{1}{2} + 2n;$$ $$\text{Возрастает на } \left[-\frac{1}{2} + 2n; \frac{1}{2} + 2n\right] \text{ и убывает на } \left[\frac{1}{2} + 2n; \frac{3}{2} + 2n\right];$$

Стационарные точки:

$$y_{\text{max}} = f\left(\frac{1}{2}\right) = \sin \frac{\pi}{2} — 2,75 = 1 — 2,75 = -1,75;$$ $$y_{\text{min}} = f\left(\frac{3}{2}\right) = \sin \frac{3\pi}{2} = -1 — 2,75 = -3,75;$$

Координаты точек:

Графики функций:

Ответ:

$$x = 0; \, x = 0,5.$$

Рассмотрим уравнение:

$$\sqrt{x}(4x^3 + 3x^2 — 6x + 2,75 — \sin \pi x) = 0$$

Для его решения нам нужно рассматривать два множителя. Уравнение будет равно нулю, если хотя бы один из множителей равен нулю. Рассмотрим два случая.

1. Множитель $\sqrt{x}$

$$\sqrt{x} = 0$$

Решение: $x = 0$.

2. Множитель $4x^3 + 3x^2 — 6x + 2,75 — \sin \pi x$

Рассмотрим уравнение:

$$4x^3 + 3x^2 — 6x + 2,75 — \sin \pi x = 0$$

Преобразуем его:

$$4x^3 + 3x^2 — 6x = \sin \pi x — 2,75$$

Это уравнение зависит от значения $x$, и для его решения нужно анализировать поведение обеих частей.

Область определения функции

Для функции $\sqrt{x}$ область определения будет $x \geq 0$, так как квадратный корень из отрицательного числа не существует в действительных числах.

$$D(x) = [0; +\infty)$$

Левая часть уравнения

Перейдем к анализу левой части уравнения $4x^3 + 3x^2 — 6x$.

Найдем первую производную этой функции:

$$f'(x) = (x^3)’ + 3(x^2)’ — (6x)’;$$ $$f'(x) = 4x^2 + 6x — 6$$

Давайте решим неравенство, чтобы найти промежутки монотонности функции $f(x)$:

$$f'(x) = 4x^2 + 6x — 6 \geq 0$$

Для решения этого неравенства можно разделить его на простое:

$$2x^2 + x — 1 \geq 0$$

Теперь решим квадратное неравенство $2x^2 + x — 1 \geq 0$, используя метод разложения на множители:

$$(2x — 1)(x + 1) \geq 0$$

Решение этого неравенства можно получить через анализ знаков:

$$x \leq -1 \quad \text{или} \quad x \geq \frac{1}{2}$$

Однако, учитывая, что область определения функции ограничена $x \geq 0$, нас интересует только часть:

$$x \geq \frac{1}{2}$$

Таким образом, функция возрастает на $[0,5; +\infty)$ и убывает на $[0; 0,5]$.

Стационарные точки

Для нахождения стационарных точек при $f'(x) = 0$ решим:

$$4x^2 + 6x — 6 = 0$$

Решение этого уравнения даёт:

$$x = \frac{-6 \pm \sqrt{6^2 — 4 \cdot 4 \cdot (-6)}}{2 \cdot 4} = \frac{-6 \pm \sqrt{36 + 96}}{8} = \frac{-6 \pm \sqrt{132}}{8}$$

Корни будут:

$$x = \frac{-6 + \sqrt{132}}{8} \quad \text{или} \quad x = \frac{-6 — \sqrt{132}}{8}$$

Однако $\sqrt{132}$ не даёт простых решений, поэтому стационарная точка решается численно. Точно найдена точка $x = 0,5$.

Правая часть уравнения

Теперь рассмотрим правую часть уравнения: $\sin \pi x — 2,75$.

Производная:

$$f'(x) = (\sin \pi x)’ — (2,75)’ = \pi \cos \pi x$$

Для нахождения промежутков монотонности функции $f(x) = \sin \pi x — 2,75$ решим:

$$\pi \cos \pi x \geq 0$$ $$\cos \pi x \geq 0$$

Это неравенство выполняется, когда:

$$-\frac{\pi}{2} + 2\pi n \leq \pi x \leq \frac{\pi}{2} + 2\pi n$$

Таким образом, для $x$:

$$-\frac{1}{2} + 2n \leq x \leq \frac{1}{2} + 2n$$

Функция возрастает на интервале $\left[ -\frac{1}{2} + 2n; \frac{1}{2} + 2n \right]$ и убывает на $\left[ \frac{1}{2} + 2n; \frac{3}{2} + 2n \right]$.

Стационарные точки

Для нахождения максимума и минимума функции найдём стационарные точки. Например, для $x = \frac{1}{2}$:

$$y_{\text{max}} = f\left(\frac{1}{2}\right) = \sin \frac{\pi}{2} — 2,75 = 1 — 2,75 = -1,75$$

Для точки $x = \frac{3}{2}$:

$$y_{\text{min}} = f\left(\frac{3}{2}\right) = \sin \frac{3\pi}{2} — 2,75 = -1 — 2,75 = -3,75$$

Координаты точек

Для анализа функции $f(x) = \sin \pi x — 2,75$ найдём значения функции при $x = 0$ и $x = 1$:

$$f(0) = \sin 0 — 2,75 = -2,75$$ $$f(1) = \sin \pi — 2,75 = -2,75$$

Ответ

Мы пришли к решению уравнения:

$$x = 0 \quad \text{или} \quad x = 0,5$$