ГДЗ по Алгебре 10 Класс Номер 45.2 Профильный Уровень Мордкович — Подробные Ответы

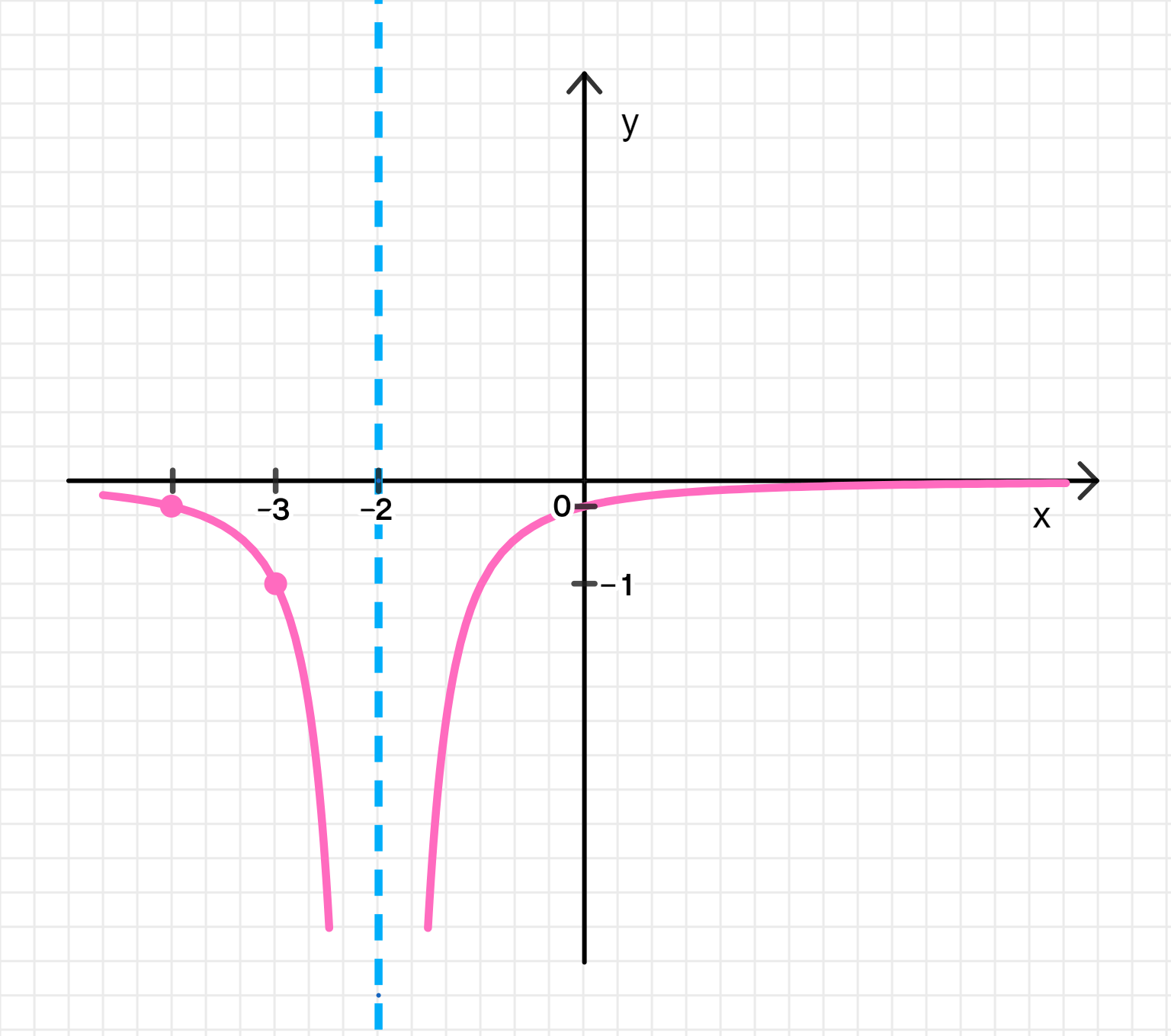
а) $f(x) = -\frac{1}{x^2 + 4x + 4} = -\frac{1}{(x+2)^2}$;

$f'(x) = \frac{(-1)(x+2)^2 + 1(x+2)^2}{(x+2)^4} = \frac{0 + 2(x+2)}{(x+2)^4} = \frac{2}{(x+2)^3}$

Область определения функции:

$$x + 2 \neq 0, \text{ отсюда } x \neq -2;$$ $$D(f) = (-\infty; -2) \cup (-2; +\infty);$$

Исследуем функцию на четность:

$$f(-x) = \frac{-1}{(-x+2)^2} = \frac{-1}{4-4x+x^2} \quad \text{нет};$$

Уравнения асимптот:

$$x = -2;$$ $$y = \lim_{x \to \infty} \frac{-1}{x^2 + 4x + 4} = \lim_{x \to \infty} \frac{-\frac{1}{x^2}}{1 + \frac{4}{x} + \frac{4}{x^2}} = \frac{-0}{1 + 0 + 0} = -0;$$

Промежутки монотонности:

$$\frac{2}{(x+2)^3} > 0;$$ $$(x+2)^3 > 0;$$ $$x + 2 > 0, \text{ отсюда } x > -2;$$

Возрастает на $(-2; +\infty)$ и убывает на $(-\infty; -2)$;

Координаты точек:

$$\begin{array}{c|c|c|c|c} x & -4 & -3 & -1 & 0 \\ \hline y & -0.25 & -1 & -1 & -0.25 \\ \end{array}$$

График функции:

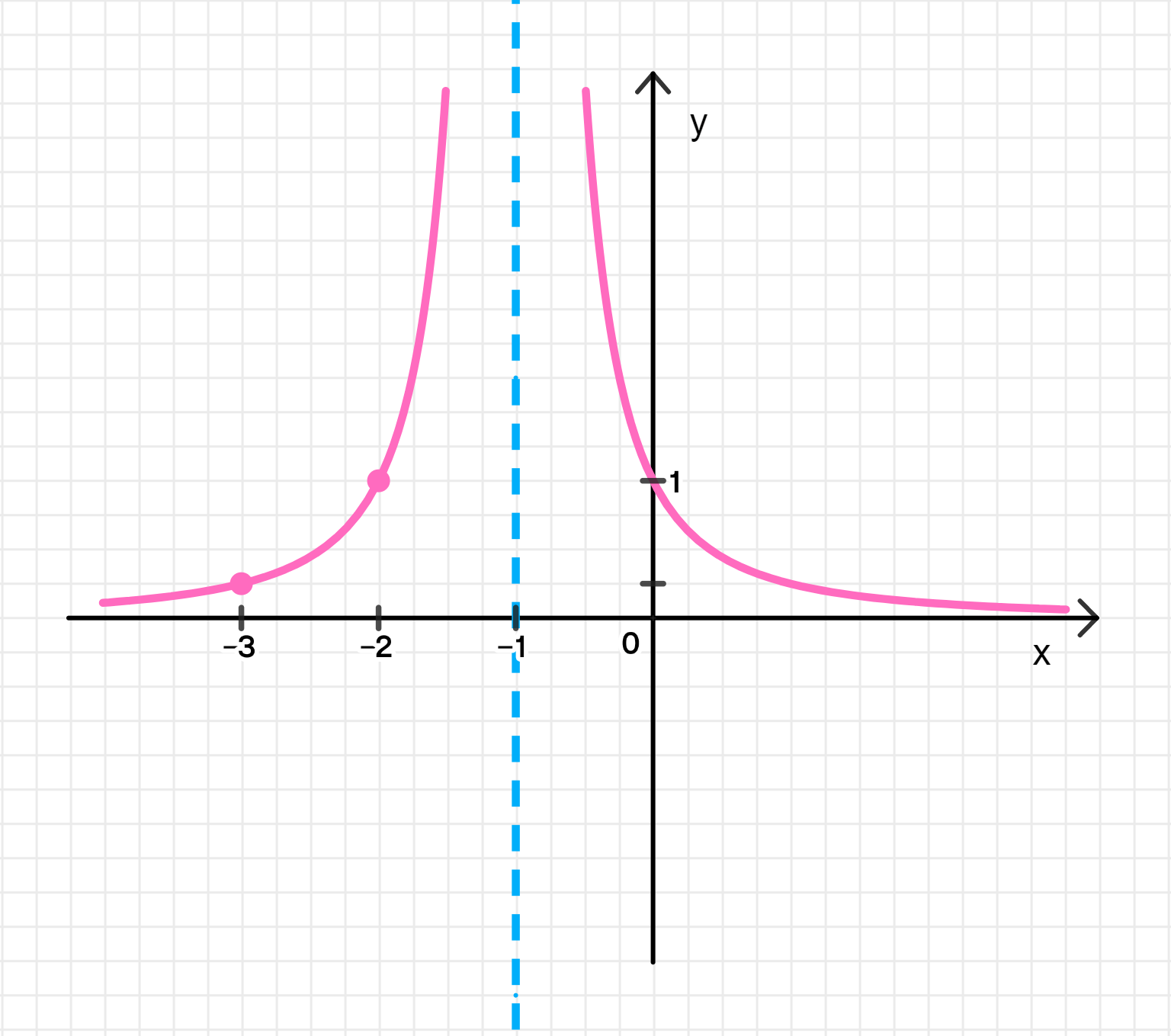
б) $f(x) = \frac{1}{x^2 + 2x + 1} = \frac{1}{(x+1)^2}$;

$f'(x) = \frac{(1)(x+1)^2 — 1(x+1)^2}{(x+1)^4} = \frac{0 — (x+1)}{(x+1)^4} = \frac{-1}{(x+1)^3}$

Область определения функции:

$$x + 1 \neq 0, \text{ отсюда } x \neq -1;$$ $$D(f) = (-\infty; -1) \cup (-1; +\infty);$$

Исследуем функцию на четность:

$$f(-x) = \frac{1}{(-x+1)^2} = \frac{1}{1-2x+x^2} \quad \text{нет};$$

Уравнения асимптот:

$$x = -1;$$ $$y = \lim_{x \to \infty} \frac{1}{x^2 + 2x + 1} = \lim_{x \to \infty} \frac{\frac{1}{x^2}}{1 + \frac{2}{x} + \frac{1}{x^2}} = \frac{0}{1 + 0 + 0} = 0;$$

Промежутки монотонности:

$$\frac{-1}{(x+1)^3} > 0;$$ $$-(x+1)^3 > 0;$$ $$x + 1 < 0, \text{ отсюда } x < -1;$$

Возрастает на $(-\infty; -1)$ и убывает на $(-1; +\infty)$;

Координаты точек:

$$\begin{array}{c|c|c|c|c} x & -3 & -2 & 0 & 1 \\ \hline y & 0.25 & 1 & 1 & 0.25 \\ \end{array}$$

График функции:

а) $f(x) = -\frac{1}{x^2 + 4x + 4} = -\frac{1}{(x+2)^2}$

Область определения функции:

Рассмотрим функцию $f(x) = -\frac{1}{(x+2)^2}$. Чтобы найти область определения, необходимо, чтобы знаменатель $(x+2)^2$ был ненулевым, так как деление на ноль невозможно.

$$(x+2)^2 \neq 0$$

Отсюда получаем:

$$x + 2 \neq 0 \quad \text{или} \quad x \neq -2$$

Таким образом, область определения функции $f(x)$ будет:

$$D(f) = (-\infty; -2) \cup (-2; +\infty)$$

Исследуем функцию на четность:

Проверим, является ли функция $f(x)$ четной. Для этого необходимо вычислить $f(-x)$ и сравнить его с $f(x)$.

$$f(-x) = -\frac{1}{(-x+2)^2} = -\frac{1}{(2-x)^2}$$

Так как $f(x) = -\frac{1}{(x+2)^2}$, мы видим, что $f(-x) \neq f(x)$. Следовательно, функция не является четной.

Уравнения асимптот:

Для поиска вертикальных и горизонтальных асимптот рассмотрим пределы функции при $x \to \infty$ и $x \to -2$.

• Вертикальная асимптота: Она будет в точке $x = -2$, так как $(x + 2)^2 = 0$ при $x = -2$, а дробь становится бесконечно большой. Таким образом, вертикальная асимптота — это линия $x = -2$.
• Горизонтальная асимптота: Для поиска горизонтальной асимптоты вычислим предел функции при $x \to \infty$:

  $$\lim_{x \to \infty} f(x) = \lim_{x \to \infty} -\frac{1}{(x+2)^2} = 0$$

  Таким образом, горизонтальная асимптота — это линия $y = 0$.

Промежутки монотонности:

Для исследования монотонности функции нужно найти производную $f'(x)$ и изучить её знак.

Производная функции $f(x) = -\frac{1}{(x+2)^2}$ будет:

$$f'(x) = \frac{d}{dx} \left( -\frac{1}{(x+2)^2} \right)$$

Применим правило дифференцирования функции вида $\frac{1}{g(x)}$, где $g(x) = (x+2)^2$:

$$f'(x) = \frac{-(-1)(x+2)^2 + 1 \cdot 2(x+2)}{(x+2)^4} = \frac{2}{(x+2)^3}$$

Теперь рассмотрим знак производной:

$$\frac{2}{(x+2)^3}$$

Чтобы эта величина была положительной, выражение $(x+2)^3$ должно быть положительным, что означает:

$$x + 2 > 0 \quad \text{или} \quad x > -2$$

Таким образом, функция возрастает на интервале $(-2; +\infty)$ и убывает на интервале $(-\infty; -2)$.

Координаты точек:

Вычислим значения функции в нескольких точках, чтобы получить таблицу координат.

Для $x = -4$:

$$f(-4) = -\frac{1}{(-4+2)^2} = -\frac{1}{(-2)^2} = -\frac{1}{4} = -0.25$$

Для $x = -3$:

$$f(-3) = -\frac{1}{(-3+2)^2} = -\frac{1}{(-1)^2} = -1$$

Для $x = -1$:

$$f(-1) = -\frac{1}{(-1+2)^2} = -\frac{1}{1^2} = -1$$

Для $x = 0$:

$$f(0) = -\frac{1}{(0+2)^2} = -\frac{1}{2^2} = -\frac{1}{4} = -0.25$$

Таким образом, таблица координат будет следующей:

$$\begin{array}{c|c|c|c|c} x & -4 & -3 & -1 & 0 \\ \hline y & -0.25 & -1 & -1 & -0.25 \\ \end{array}$$

График функции:

б) $f(x) = \frac{1}{x^2 + 2x + 1} = \frac{1}{(x+1)^2}$

Область определения функции:

Рассмотрим функцию $f(x) = \frac{1}{(x+1)^2}$. Чтобы найти область определения, необходимо, чтобы знаменатель $(x+1)^2$ был ненулевым:

$$(x+1)^2 \neq 0$$

Отсюда получаем:

$$x + 1 \neq 0 \quad \text{или} \quad x \neq -1$$

Таким образом, область определения функции $f(x)$ будет:

$$D(f) = (-\infty; -1) \cup (-1; +\infty)$$

Исследуем функцию на четность:

Проверим, является ли функция $f(x)$ четной. Для этого необходимо вычислить $f(-x)$ и сравнить его с $f(x)$.

$$f(-x) = \frac{1}{(-x+1)^2} = \frac{1}{(1-2x+x^2)}$$

Мы видим, что $f(-x) \neq f(x)$, значит, функция не является четной.

Уравнения асимптот:

• Вертикальная асимптота: Она будет в точке $x = -1$, так как $(x+1)^2 = 0$ при $x = -1$.
• Горизонтальная асимптота: Для поиска горизонтальной асимптоты вычислим предел функции при $x \to \infty$:

  $$\lim_{x \to \infty} f(x) = \lim_{x \to \infty} \frac{1}{(x+1)^2} = 0$$

  Таким образом, горизонтальная асимптота — это линия $y = 0$.

Промежутки монотонности:

Для исследования монотонности функции нужно найти производную $f'(x)$ и изучить её знак.

Производная функции $f(x) = \frac{1}{(x+1)^2}$ будет:

$$f'(x) = -\frac{2}{(x+1)^3}$$

Рассмотрим знак производной:

$$f'(x) > 0 \quad \text{для} \quad x < -1$$ $$f'(x) < 0 \quad \text{для} \quad x > -1$$

Таким образом, функция возрастает на интервале $(-\infty; -1)$ и убывает на интервале $(-1; +\infty)$.

Координаты точек:

Для $x = -3$:

$$f(-3) = \frac{1}{(-3+1)^2} = \frac{1}{(-2)^2} = \frac{1}{4} = 0.25$$

Для $x = -2$:

$$f(-2) = \frac{1}{(-2+1)^2} = \frac{1}{(-1)^2} = 1$$

Для $x = 0$:

$$f(0) = \frac{1}{(0+1)^2} = \frac{1}{1^2} = 1$$

Для $x = 1$:

$$f(1) = \frac{1}{(1+1)^2} = \frac{1}{2^2} = \frac{1}{4} = 0.25$$

Таким образом, таблица координат будет следующей:

$$\begin{array}{c|c|c|c|c} x & -3 & -2 & 0 & 1 \\ \hline y & 0.25 & 1 & 1 & 0.25 \\ \end{array}$$

График функции: