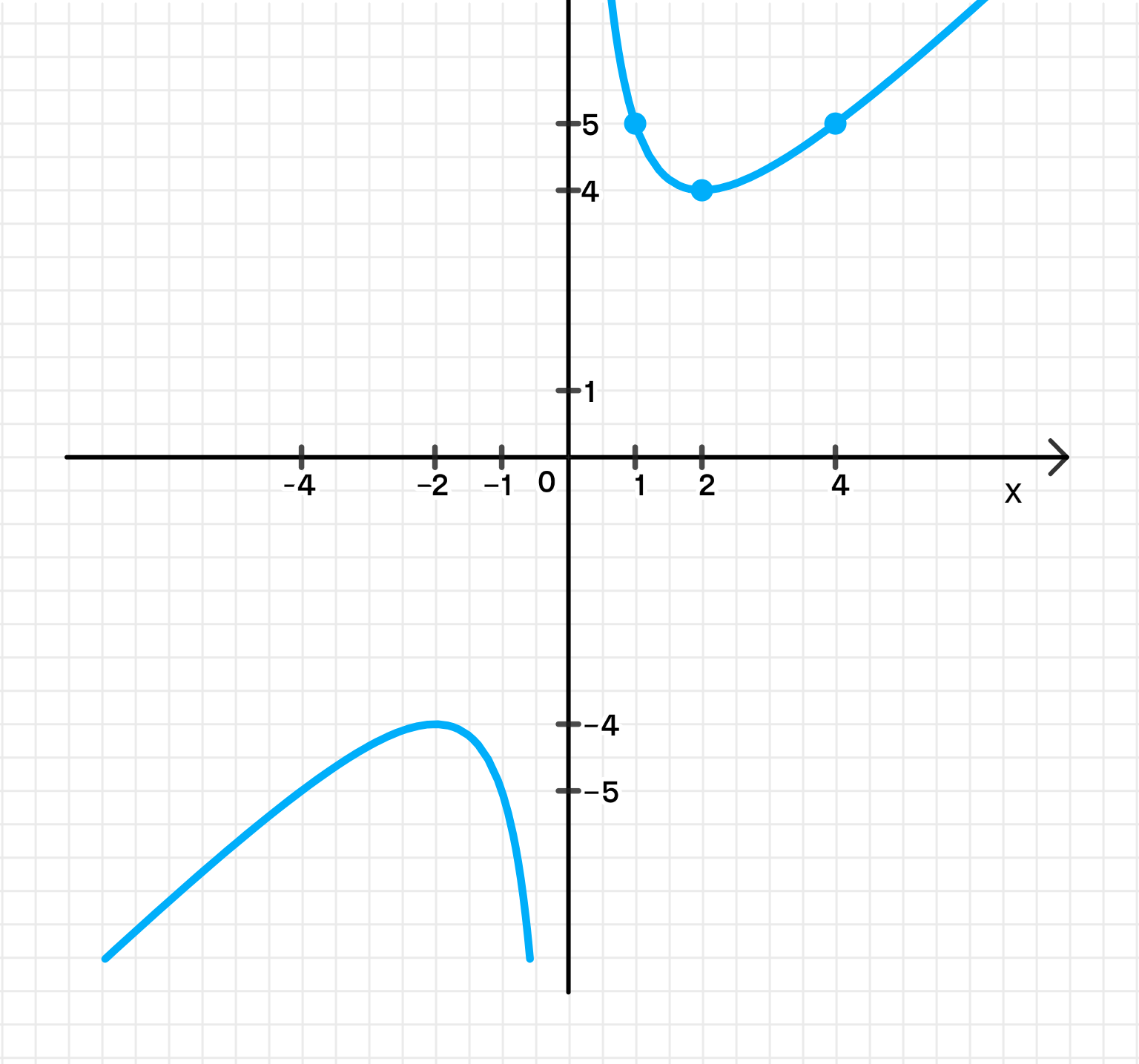ГДЗ по Алгебре 10 Класс Номер 45.3 Профильный Уровень Мордкович — Подробные Ответы

Исследуйте функцию и постройте ее график:

а) $f(x)=\frac{x}{2}+\frac{2}{x}$;

б) $f(x)=\frac{x^2+4}{x}$

а) $f(x)=\frac{x}{2}+\frac{2}{x}$;

$f^{\mathrm{\prime }}(x)=\frac{1}{2}(x{)}^{\mathrm{\prime }}+2{\left(\frac{1}{x}\right)}^{\mathrm{\prime }}=\frac{1}{2}-\frac{2}{x^2};$

Область определения функции:

$$x\mathrm{\ne }0;$$$$D(f)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty });$$

Исследуем функцию на четность:

$$f(-x)=\frac{-x}{2}+\frac{2}{-x}=-(\frac{x}{2}+\frac{2}{x})=-f(x)\text{(нечетная)};$$

Уравнения асимптот:

$$x=0;$$$$y=\underset{x\to \mathrm{\infty }}{\lim }\frac{x}{2}+\frac{2}{x}=+\mathrm{\infty }+0=+\mathrm{\infty }\text{(не существует)};$$

Промежутки монотонности:

$$\frac{1}{2}-\frac{2}{x^2}\ge 0;$$$$\frac{x^2-4}{2x^2}\ge 0;$$$$x^2-4\ge 0;$$$$x^2\ge 4,\text{ отсюда }x\le -2\text{ или }x\ge 2;$$

Возрастает на $(-\mathrm{\infty };-2]\cup [-2;+\mathrm{\infty })$ и убывает на $[-2;0)\cup (0;2]$;

Стационарные точки:

$$y_{\max }=f(-2)=\frac{-2}{2}+\frac{2}{-2}=-1-1=-2;$$$$y_{\min }=f(2)=\frac{2}{2}+\frac{2}{2}=1+1=2;$$

Координаты точек:

$$\overline{)\begin{array}{ccccc}x& 0,5& 1& 3& 5\\ y& 4,25& 2,5& 2,2& 2,9\end{array}}$$

График функции:

б) $f(x)=\frac{x^2+4}{x}=x+\frac{4}{x}$;

$f^{\mathrm{\prime }}(x)=(x{)}^{\mathrm{\prime }}+4{\left(\frac{1}{x}\right)}^{\mathrm{\prime }}=1-\frac{4}{x^2};$

Область определения функции:

$$x\mathrm{\ne }0;$$$$D(f)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty });$$

Исследуем функцию на четность:

$$f(-x)=-x+\frac{4}{-x}=-(x+\frac{4}{x})=-f(x)\text{(нечетная)};$$

Уравнения асимптот:

$$x=0;$$$$y=\underset{x\to \mathrm{\infty }}{\lim }x+\frac{4}{x}=+\mathrm{\infty }+0=+\mathrm{\infty }\text{(не существует)};$$

Промежутки монотонности:

$$1-\frac{4}{x^2}\ge 0;$$$$\frac{x^2-4}{x^2}\ge 0;$$$$x^2-4\ge 0;$$$$x^2\ge 4,\text{ отсюда }x\le -2\text{ или }x\ge 2;$$

Возрастает на $(-\mathrm{\infty };-2]\cup [-2;+\mathrm{\infty })$ и убывает на $[-2;0)\cup (0;2]$;

Стационарные точки:

$$y_{\max }=f(-2)=-2+\frac{4}{-2}=-2-2=-4;$$$$y_{\min }=f(2)=2+\frac{4}{2}=2+2=4;$$

Координаты точек:

$$\overline{)\begin{array}{cccc}x& 1& 4& 6\\ y& 5& 2,9& 6,6\end{array}}$$

График функции:

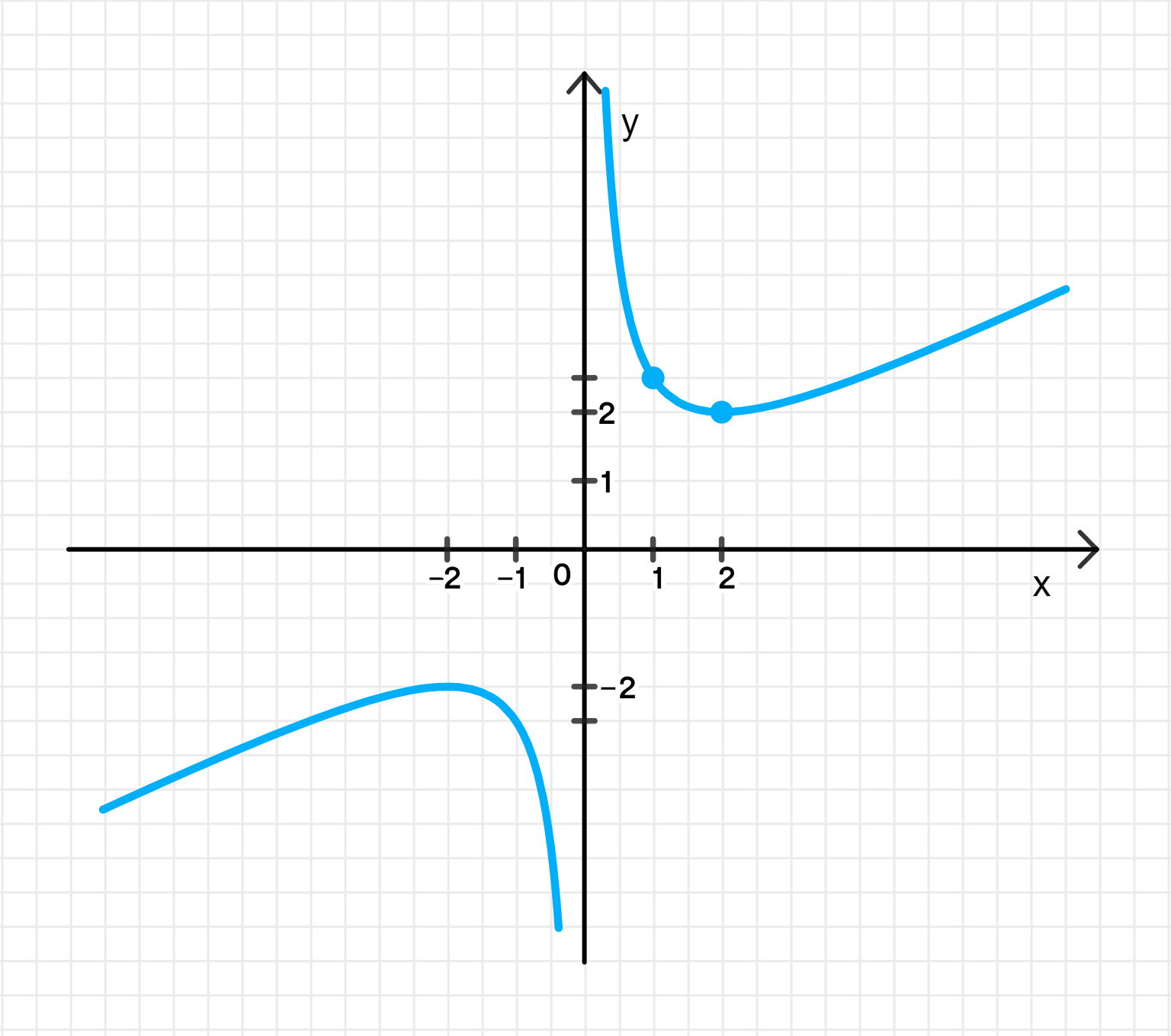
а) $f(x)=\frac{x}{2}+\frac{2}{x}$

Область определения функции:

Рассмотрим функцию $f(x)=\frac{x}{2}+\frac{2}{x}$.

Чтобы найти область определения, необходимо, чтобы знаменатель $x$ в дроби $\frac{2}{x}$ был ненулевым. Таким образом, $x\mathrm{\ne }0$.

Следовательно, область определения функции:

$$D(f)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$$

Это означает, что функция определена для всех значений $x$, кроме $x=0$.

Исследуем функцию на четность:

Проверим, является ли функция $f(x)$ четной. Для этого вычислим $f(-x)$ и сравним его с $f(x)$.

$$f(-x)=\frac{-x}{2}+\frac{2}{-x}=-(\frac{x}{2}+\frac{2}{x})=-f(x)$$

Это означает, что функция $f(x)$ является нечетной, так как $f(-x)=-f(x)$.

Уравнения асимптот:

Теперь найдем асимптоты функции.

• Вертикальная асимптота: Функция имеет вертикальную асимптоту, если знаменатель функции равен нулю. Мы уже знаем, что $x=0$ является точкой, в которой знаменатель $x$ в дроби $\frac{2}{x}$ становится равным нулю. Таким образом, вертикальная асимптота находится в точке $x=0$.
• Горизонтальная асимптота: Чтобы найти горизонтальную асимптоту, нужно вычислить предел функции при $x\to \mathrm{\infty }$ и $x\to -\mathrm{\infty }$.Рассмотрим предел при $x\to \mathrm{\infty }$:

  $$\underset{x\to \mathrm{\infty }}{\lim }(\frac{x}{2}+\frac{2}{x})=\underset{x\to \mathrm{\infty }}{\lim }\frac{x}{2}+\underset{x\to \mathrm{\infty }}{\lim }\frac{2}{x}=+\mathrm{\infty }+0=+\mathrm{\infty }$$

  Таким образом, горизонтальная асимптота отсутствует, так как предел стремится к бесконечности.

  Точно так же, при $x\to -\mathrm{\infty }$, функция также стремится к бесконечности:

  $$\underset{x\to -\mathrm{\infty }}{\lim }(\frac{x}{2}+\frac{2}{x})=-\mathrm{\infty }+0=-\mathrm{\infty }$$

  Таким образом, горизонтальная асимптота также отсутствует.

Промежутки монотонности:

Для исследования монотонности функции найдем её производную $f^{\mathrm{\prime }}(x)$. Используя правила дифференцирования, получаем:

$$f^{\mathrm{\prime }}(x)=\frac{d}{dx}(\frac{x}{2}+\frac{2}{x})=\frac{1}{2}-\frac{2}{x^2}$$

Теперь исследуем знак производной. Для этого решим неравенство $f^{\mathrm{\prime }}(x)\ge 0$:

$$\frac{1}{2}-\frac{2}{x^2}\ge 0$$

Преобразуем неравенство:

$$\frac{x^2-4}{2x^2}\ge 0$$

Умножим обе части неравенства на $2x^2$ (при этом учитываем, что $x^2\ge 0$):

$$x^2-4\ge 0$$

Разрешим это неравенство:

$$x^2\ge 4$$

Это приводит к двум промежуткам:

$$x\le -2\text{или}x\ge 2$$

Таким образом, функция возрастает на интервале $(-\mathrm{\infty };-2]\cup [2;+\mathrm{\infty })$ и убывает на интервале $[-2;0)\cup (0;2]$.

Стационарные точки:

Для нахождения стационарных точек приравняем производную к нулю:

$$f^{\mathrm{\prime }}(x)=0\Rightarrow \frac{1}{2}-\frac{2}{x^2}=0$$

Решаем это уравнение:

$$\frac{2}{x^2}=\frac{1}{2}\Rightarrow x^2=4$$

Таким образом, $x=-2$ и $x=2$ — стационарные точки.

Теперь найдем значения функции в этих точках:

$$y_{\max }=f(-2)=\frac{-2}{2}+\frac{2}{-2}=-1-1=-2$$$$y_{\min }=f(2)=\frac{2}{2}+\frac{2}{2}=1+1=2$$

Координаты точек:

Рассчитаем значения функции для различных значений $x$:

Для $x=0.5$:

$$f(0.5)=\frac{0.5}{2}+\frac{2}{0.5}=0.25+4=4.25$$

Для $x=1$:

$$f(1)=\frac{1}{2}+\frac{2}{1}=0.5+2=2.5$$

Для $x=3$:

$$f(3)=\frac{3}{2}+\frac{2}{3}=1.5+0.6667=2.1667\approx 2.2$$

Для $x=5$:

$$f(5)=\frac{5}{2}+\frac{2}{5}=2.5+0.4=2.9$$

Таким образом, таблица координат будет следующей:

$$\overline{)\begin{array}{ccccc}x& 0.5& 1& 3& 5\\ y& 4.25& 2.5& 2.2& 2.9\end{array}}$$

График функции:

б) $f(x)=\frac{x^2+4}{x}=x+\frac{4}{x}$

Область определения функции:

Рассмотрим функцию $f(x)=x+\frac{4}{x}$.

Аналогично первому примеру, функция будет определена при $x\mathrm{\ne }0$, так как знаменатель $x$ в дроби $\frac{4}{x}$ не может быть равен нулю.

Таким образом, область определения:

$$D(f)=(-\mathrm{\infty };0)\cup (0;+\mathrm{\infty })$$

Исследуем функцию на четность:

Проверим, является ли функция $f(x)$ четной:

$$f(-x)=-x+\frac{4}{-x}=-(x+\frac{4}{x})=-f(x)$$

Это означает, что функция $f(x)$ также является нечетной.

Уравнения асимптот:

• Вертикальная асимптота: Функция имеет вертикальную асимптоту в точке $x=0$, так как $\frac{4}{x}$ становится неопределенной при $x=0$.
• Горизонтальная асимптота: Рассмотрим предел функции при $x\to \mathrm{\infty }$ и $x\to -\mathrm{\infty }$:$$\underset{x\to \mathrm{\infty }}{\lim }(x+\frac{4}{x})=\underset{x\to \mathrm{\infty }}{\lim }x+\underset{x\to \mathrm{\infty }}{\lim }\frac{4}{x}=\mathrm{\infty }+0=\mathrm{\infty }$$

  То же самое при $x\to -\mathrm{\infty }$:

  $$\underset{x\to -\mathrm{\infty }}{\lim }(x+\frac{4}{x})=-\mathrm{\infty }+0=-\mathrm{\infty }$$

  Горизонтальная асимптота отсутствует.

Промежутки монотонности:

Найдем производную:

$$f^{\mathrm{\prime }}(x)=1-\frac{4}{x^2}$$

Теперь исследуем знак производной:

$$1-\frac{4}{x^2}\ge 0\Rightarrow \frac{x^2-4}{x^2}\ge 0$$

Решаем:

$$x^2-4\ge 0\Rightarrow x^2\ge 4$$

То есть:

$$x\le -2\text{или}x\ge 2$$

Таким образом, функция возрастает на интервале $(-\mathrm{\infty };-2]\cup [2;+\mathrm{\infty })$ и убывает на интервале $[-2;0)\cup (0;2]$.

Стационарные точки:

Приравняем производную к нулю:

$$1-\frac{4}{x^2}=0\Rightarrow x^2=4$$

Таким образом, $x=-2$ и $x=2$ — стационарные точки.

Найдем значения функции в этих точках:

$$y_{\max }=f(-2)=-2+\frac{4}{-2}=-2-2=-4$$$$y_{\min }=f(2)=2+\frac{4}{2}=2+2=4$$

Координаты точек:

Для $x=1$:

$$f(1)=1+\frac{4}{1}=1+4=5$$

Для $x=4$:

$$f(4)=4+\frac{4}{4}=4+1=5$$

Для $x=6$:

$$f(6)=6+\frac{4}{6}=6+0.6667=6.6667\approx 6.6$$

Таким образом, таблица координат:

$$\overline{)\begin{array}{cccc}x& 1& 4& 6\\ y& 5& 2.9& 6.6\end{array}}$$

График функции: