ГДЗ по Алгебре 10 Класс Номер 45.8 Профильный Уровень Мордкович — Подробные Ответы

а) $f(x) = 2\sqrt{x} — x$;

$f'(x) = 2(\sqrt{x})’ — (x)’ = \frac{2}{2\sqrt{x}} — 1 = \frac{1}{\sqrt{x}} — 1;$

Область определения функции:

$$x \geq 0;$$

$D(f) = [0; +\infty);$

Исследуем функцию на четность:

$$f(-x) = 2\sqrt{-x} + x \quad \text{— нет};$$

Уравнения асимптот:

$$y = \lim_{x \to \infty} 2\sqrt{x} — x = -\infty \quad \text{— не существует};$$

Промежутки монотонности:

$$\frac{1}{\sqrt{x}} — 1 \geq 0;$$ $$1 — \sqrt{x} \geq 0;$$ $$1 — x^2 \geq 0;$$ $$1 \geq x^2, \quad \text{отсюда } -1 \leq x \leq 1;$$

Возрастает на $[0; 1]$ и убывает на $[1; +\infty)$;

Стационарные точки:

$$y_{\max} = f(1) = 2\sqrt{1} — 1 = 2 — 1 = 1;$$

Координаты точек:

$$\begin{array}{c|c c c c} x & 0 & 0,25 & 2 & 4 & 9 \\ \hline y & 0 & 0,75 & 0,8 & 0 & -3 \\ \end{array}$$

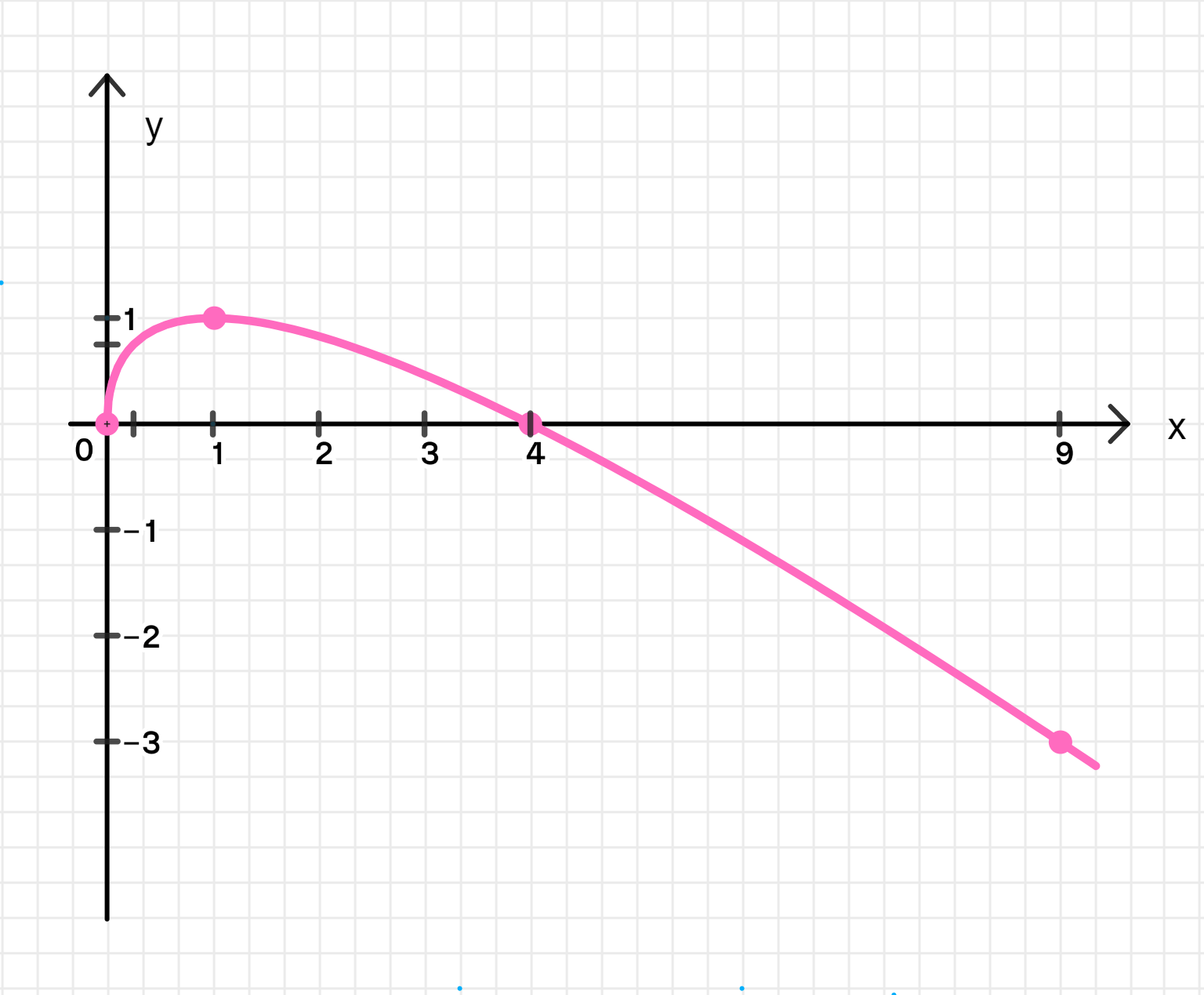
График функции:

б) $f(x) = \sqrt{x+4} + \frac{2}{3}\sqrt{9-3x}$;

$f'(x) = (\sqrt{x+4})’ + \frac{2}{3}(\sqrt{9-3x})’;$

$f'(x) = \frac{1}{2\sqrt{x+4}} — \frac{2}{3} \cdot \frac{1}{2\sqrt{9-3x}} = \frac{1}{2\sqrt{x+4}} — \frac{1}{\sqrt{9-3x}};$

Область определения функции:

$$x + 4 \geq 0, \quad \text{отсюда } x \geq -4;$$ $$9 — 3x \geq 0, \quad \text{отсюда } x \leq 3;$$

$D(f) = [-4; 3];$

Исследуем функцию на четность:

$$f(-x) = \sqrt{-x+4} + \frac{2}{3}\sqrt{9+3x} \quad \text{— нет};$$

Уравнения асимптот:

$$y = \lim_{x \to \infty} \sqrt{x+4} + \frac{2}{3}\sqrt{9-3x} = -\infty \quad \text{— не существует};$$

Промежутки монотонности:

$$\frac{1}{2\sqrt{x+4}} — \frac{1}{\sqrt{9-3x}} \geq 0;$$ $$\frac{\sqrt{9-3x} — 2\sqrt{x+4}}{2\sqrt{x+4} \cdot \sqrt{9-3x}} \geq 0;$$ $$\sqrt{9-3x} — 2\sqrt{x+4} \geq 0;$$ $$9 — 3x — 4(x + 4) \geq 0;$$ $$9 — 3x — 4x — 16 \geq 0;$$ $$-7 \geq 7x, \quad \text{отсюда } x \leq -1;$$

Возрастает на $[-4; -1]$ и убывает на $[-1; 3]$;

Стационарные точки:

$$y_{\max }=f(-1)=\sqrt{3}+\frac{2}{3}\sqrt{12}=\sqrt{3}+\frac{2}{3}\cdot 2\sqrt{3}=$$

$$y_{\max} = f(-1) = \sqrt{3} + \frac{2}{3}\sqrt{12} = \sqrt{3} + \frac{2}{3} \cdot 2\sqrt{3} = \frac{3\sqrt{3} + 4\sqrt{3}}{3} = \frac{7\sqrt{3}}{3} \approx 4;$$

Координаты точек:

$$\begin{array}{c|c|c|c|c|c} x & -4 & -2 & 0 & 2 & 3 \\ \hline y & 3 & 4 & 4 & 3.6 & 2.6 \\ \end{array}$$

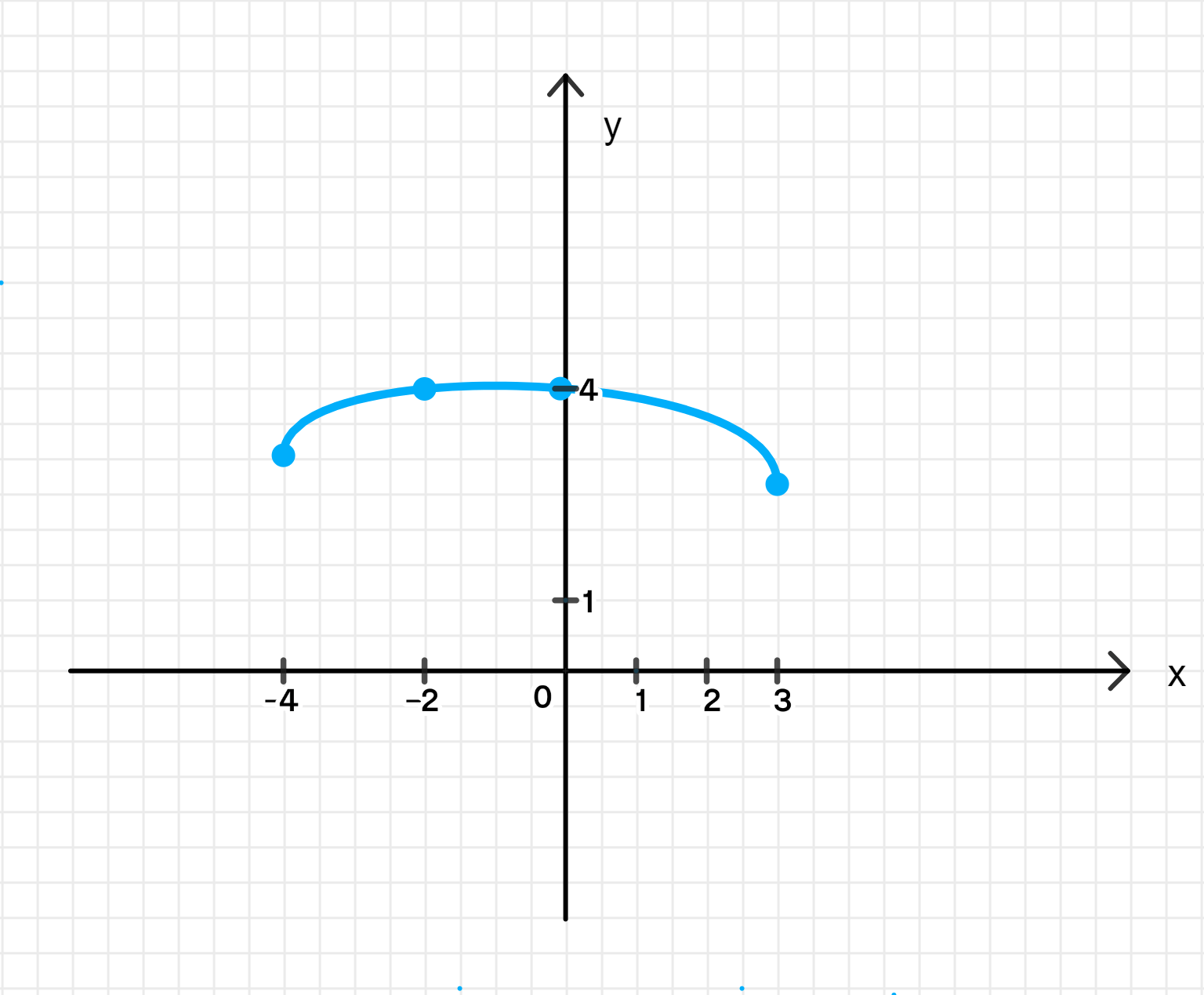
График функции:

а) $f(x) = 2\sqrt{x} — x$

1. Производная функции:

Для нахождения производной функции $f(x) = 2\sqrt{x} — x$, используем стандартные правила дифференцирования.

Дифференцируем первый член $2\sqrt{x}$. Вспомним, что производная функции $\sqrt{x}$ равна $\frac{1}{2\sqrt{x}}$. Тогда:

$$\frac{d}{dx}(2\sqrt{x}) = 2 \cdot \frac{1}{2\sqrt{x}} = \frac{1}{\sqrt{x}}$$

Дифференцируем второй член $-x$. Это стандартная производная:

$$\frac{d}{dx}(-x) = -1$$

Теперь подставим эти значения в общую формулу для производной:

$$f'(x) = \frac{1}{\sqrt{x}} — 1$$

Таким образом, производная функции:

$$f'(x) = \frac{1}{\sqrt{x}} — 1$$

2. Область определения функции:

Для нахождения области определения функции $f(x) = 2\sqrt{x} — x$, нужно, чтобы выражение под квадратным корнем было неотрицательным, то есть:

$$x \geq 0$$

Таким образом, область определения функции:

$$D(f) = [0; +\infty)$$

3. Исследуем функцию на четность:

Проверим, является ли функция четной. Для этого вычислим $f(-x)$ и сравним с $f(x)$.

$$f(-x) = 2\sqrt{-x} — (-x)$$

Но функция $\sqrt{-x}$ не существует для $x > 0$, следовательно, $f(-x)$ не существует на интервале, где $x \geq 0$. Таким образом, функция нечетная.

4. Уравнения асимптот:

Для нахождения асимптот функции $f(x) = 2\sqrt{x} — x$ рассмотрим пределы при $x \to \infty$ и $x \to 0$.

• Горизонтальная асимптота:

  Рассмотрим предел функции при $x \to \infty$:

  $$\lim_{x \to \infty} (2\sqrt{x} — x)$$

  При $x \to \infty$, член $2\sqrt{x}$ растет значительно медленнее, чем $x$, и, следовательно, функция стремится к $-\infty$. Таким образом, горизонтальная асимптота не существует.

• Вертикальная асимптота:

  Рассмотрим предел функции при $x \to 0^+$:

  $$\lim_{x \to 0^+} (2\sqrt{x} — x) = 0 — 0 = 0$$

  Следовательно, вертикальная асимптота отсутствует, так как функция в точке $x = 0$ не расходится.

5. Промежутки монотонности:

Для исследования промежутков монотонности исследуем знак производной $f'(x)$:

$$f'(x) = \frac{1}{\sqrt{x}} — 1$$

Теперь решим неравенство $f'(x) \geq 0$ для нахождения промежутков, где функция возрастает:

$$\frac{1}{\sqrt{x}} — 1 \geq 0 \quad \Rightarrow \quad \frac{1}{\sqrt{x}} \geq 1$$

Умножаем обе стороны на $\sqrt{x}$ (положительное число):

$$1 \geq \sqrt{x} \quad \Rightarrow \quad 1 \geq x$$

Таким образом, функция возрастает на интервале $[0; 1]$ и убывает на интервале $[1; +\infty)$.

6. Стационарные точки:

Стационарные точки находятся, когда производная равна нулю:

$$f'(x) = 0 \quad \Rightarrow \quad \frac{1}{\sqrt{x}} — 1 = 0 \quad \Rightarrow \quad \frac{1}{\sqrt{x}} = 1 \quad \Rightarrow \quad x = 1$$

Теперь вычислим значение функции в точке $x = 1$:

$$y_{\max} = f(1) = 2\sqrt{1} — 1 = 2 — 1 = 1$$

Таким образом, стационарная точка $x = 1$ является точкой максимума.

7. Координаты точек:

Рассчитаем значения функции в нескольких точках:

• Для $x = 0$:

$$f(0) = 2\sqrt{0} — 0 = 0$$

• Для $x = 0.25$:

$$f(0.25) = 2\sqrt{0.25} — 0.25 = 2(0.5) — 0.25 = 1 — 0.25 = 0.75$$

• Для $x = 2$:

$$f(2) = 2\sqrt{2} — 2 \approx 2(1.414) — 2 = 2.828 — 2 = 0.828$$

• Для $x = 4$:

$$f(4) = 2\sqrt{4} — 4 = 2(2) — 4 = 4 — 4 = 0$$

• Для $x = 9$:

$$f(9) = 2\sqrt{9} — 9 = 2(3) — 9 = 6 — 9 = -3$$

Таблица координат:

$$\begin{array}{|c|c|c|c|c|c} \hline x & 0 & 0.25 & 2 & 4 & 9 \\ \hline y & 0 & 0.75 & 0.828 & 0 & -3 \\ \hline \end{array}$$

8. График функции:

б) $f(x) = \sqrt{x+4} + \frac{2}{3}\sqrt{9-3x}$

1. Производная функции:

Для нахождения производной функции $f(x) = \sqrt{x+4} + \frac{2}{3}\sqrt{9-3x}$, воспользуемся правилом дифференцирования для корней:

Производная от $\sqrt{x+4}$:

$$\frac{d}{dx} \left( \sqrt{x+4} \right) = \frac{1}{2\sqrt{x+4}}$$

Производная от $\frac{2}{3} \sqrt{9-3x}$:

$$\frac{d}{dx} \left( \frac{2}{3} \sqrt{9-3x} \right) = \frac{2}{3} \cdot \frac{1}{2\sqrt{9-3x}} \cdot (-3) = -\frac{1}{\sqrt{9-3x}}$$

Теперь подставим эти значения в формулу для производной:

$$f'(x) = \frac{1}{2\sqrt{x+4}} — \frac{1}{\sqrt{9-3x}}$$

2. Область определения функции:

1. $\sqrt{x+4}$ существует, когда $x+4 \geq 0$, то есть $x \geq -4$.
2. $\sqrt{9-3x}$ существует, когда $9 — 3x \geq 0$, то есть $x \leq 3$.

Таким образом, область определения функции:

$$D(f) = [-4; 3]$$

3. Исследуем функцию на четность:

Проверим, является ли функция четной:

$$f(-x) = \sqrt{-x+4} + \frac{2}{3}\sqrt{9+3x} \quad \text{— нет};$$

Таким образом, функция не является четной.

4. Уравнения асимптот:

• Горизонтальная асимптота: Для нахождения горизонтальной асимптоты вычислим предел функции при $x \to \infty$:

$$y = \lim_{x \to \infty} \sqrt{x+4} + \frac{2}{3}\sqrt{9-3x}$$

При $x \to \infty$, первый член $\sqrt{x+4}$ растет, а второй стремится к отрицательному бесконечности, то есть функция стремится к $-\infty$, и горизонтальная асимптота не существует.

• Вертикальная асимптота: Для нахождения вертикальной асимптоты рассмотрим предел при $x \to 3^-$:

$$y = \lim_{x \to 3^-} \sqrt{x+4} + \frac{2}{3}\sqrt{9-3x} = 3 + 0 = 3$$

Таким образом, асимптот не существует.

5. Промежутки монотонности:

Исследуем знак производной $f'(x)$:

$$f'(x) = \frac{1}{2\sqrt{x+4}} — \frac{1}{\sqrt{9-3x}}$$

Для нахождения промежутков монотонности решаем неравенство $f'(x) \geq 0$:

$$\frac{1}{2\sqrt{x+4}} — \frac{1}{\sqrt{9-3x}} \geq 0$$

Преобразуем неравенство:

$$\frac{\sqrt{9-3x} — 2\sqrt{x+4}}{2\sqrt{x+4} \cdot \sqrt{9-3x}} \geq 0$$

Решаем числитель:

$$\sqrt{9-3x} — 2\sqrt{x+4} \geq 0$$

Далее, решая это неравенство, получаем $x \leq -1$.

Таким образом, функция возрастает на $[-4; -1]$ и убывает на $[-1; 3]$.

6. Стационарные точки:

Стационарные точки находятся при $x = -1$, в котором производная равна нулю. Вычислим значение функции в точке $x = -1$:

$$y_{\max }=f(-1)=\sqrt{3}+\frac{2}{3}\sqrt{12}=\sqrt{3}+\frac{2}{3}\cdot 2\sqrt{3}=\frac{3\sqrt{3}+4\sqrt{3}}{3}=$$

$$y_{\max} = f(-1) = \sqrt{3} + \frac{2}{3}\sqrt{12} = \sqrt{3} + \frac{2}{3} \cdot 2\sqrt{3} = \frac{3\sqrt{3} + 4\sqrt{3}}{3} = \frac{7\sqrt{3}}{3} \approx 4$$

7. Координаты точек:

Рассчитаем значения функции для нескольких значений $x$:

• Для $x = -4$:

$$f(-4) = \sqrt{0} + \frac{2}{3}\sqrt{21} \approx 0 + 3 \approx 3$$

• Для $x = -2$:

$$f(-2) = \sqrt{2} + \frac{2}{3}\sqrt{15} \approx 1.414 + 3.872 \approx 4.286$$

• Для $x = 0$:

$$f(0) = \sqrt{4} + \frac{2}{3}\sqrt{9} = 2 + 2 = 4$$

• Для $x = 2$:

$$f(2) = \sqrt{6} + \frac{2}{3}\sqrt{3} \approx 2.449 + 1.155 \approx 3.604$$

• Для $x = 3$:

$$f(3) = \sqrt{7} + \frac{2}{3}\sqrt{0} = 2.646 + 0 = 2.646$$

Таблица координат:

$$\begin{array}{|c|c|c|c|c|c} \hline x & -4 & -2 & 0 & 2 & 3 \\ \hline y & 3 & 4.286 & 4 & 3.604 & 2.646 \\ \hline \end{array}$$

8. График функции: