ГДЗ по Алгебре 10 Класс Номер 46.52 Профильный Уровень Мордкович — Подробные Ответы

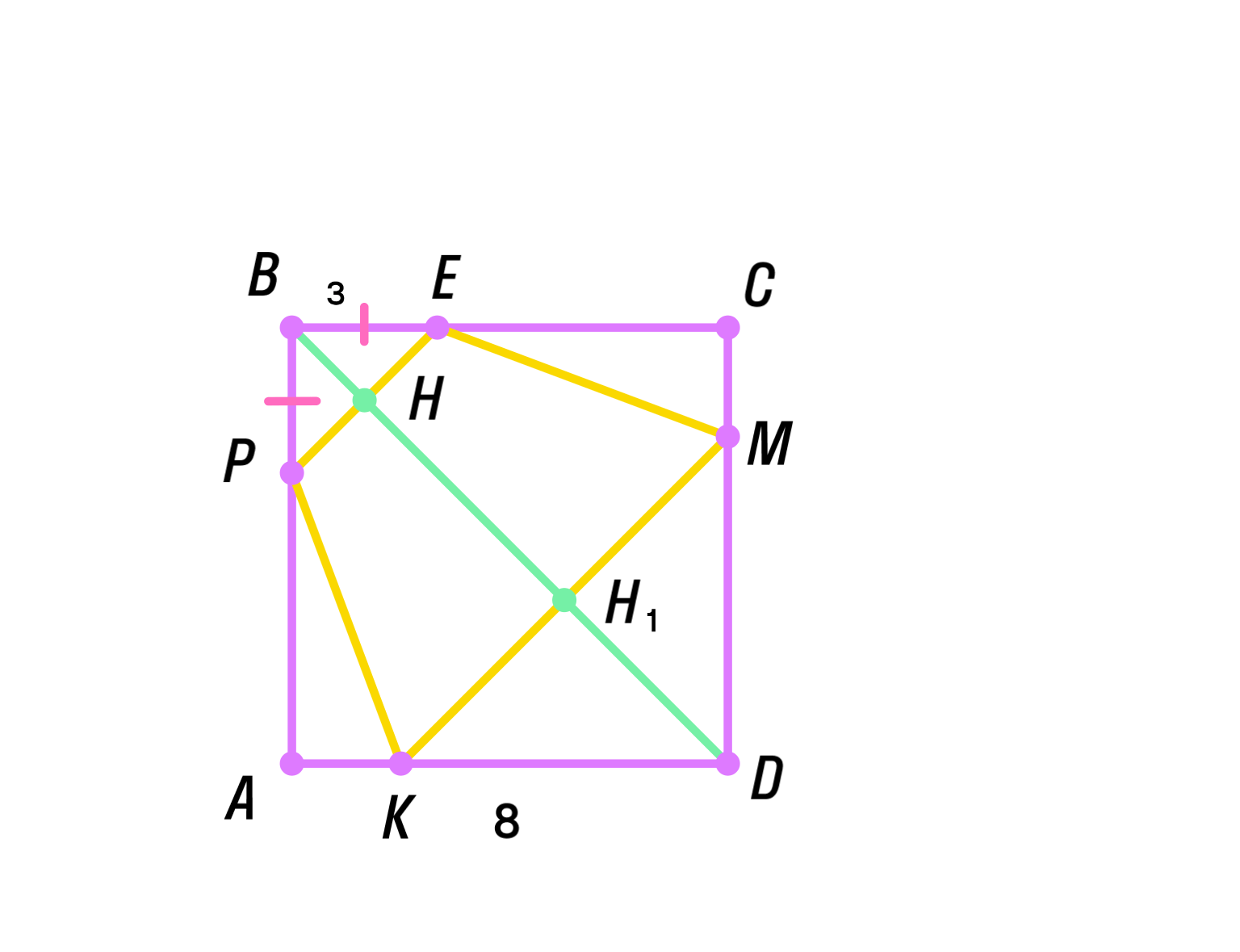
Сторона квадрата $ABCD$ равна 8 см. На сторонах $AB$ и $BC$ взяты соответственно точки $P$ и $E$ так, что $BP = BE = 3$ см. На сторонах $AD$ и $CD$ берутся точки соответственно $K$ и $M$ так, что четырёхугольник $KREM$ — трапеция. Чему равна наибольшая площадь такой трапеции?

Отобразим условие задачи:

Дано: $ABCD$ — квадрат; $AB = BC = CD = AD = 8 \, \text{см}$; $BP = BE = 3 \, \text{см}$; $K \in AD$; $M \in DC$; $KREM$ — трапеция;

Найти: наибольшую площадь трапеции;

Решение:

Рассмотрим прямоугольный треугольник $PBE$:

$$PB = BE, \text{значит } \Delta PBE \text{ — равнобедренный, тогда } \angle BPE = \angle BEP = 45^\circ;$$ $$PE = \sqrt{PB^2 + BE^2} = \sqrt{3^2 + 3^2} = \sqrt{2 \cdot 3^2} = 3\sqrt{2} \, \text{см};$$

$KREM$ — трапеция, значит отрезки $KM$ и $PE$ параллельны, тогда:

$$\angle KMD = \angle DKM = 45^\circ;$$

Рассмотрим равнобедренный и прямоугольный треугольник $KMD$:

$$\text{Пусть } MD = KD = x, \text{тогда } KM = \sqrt{KD^2 + MD^2} = \sqrt{x^2 + x^2} = \sqrt{2x^2} = x\sqrt{2};$$

Проведем диагональ $BD$ квадрата и отметим точки $H$ и $H_1$ на пересечении этой диагонали с отрезками $PE$ и $KM$ соответственно:

$$BD = \sqrt{8^2 + 8^2} = \sqrt{2 \cdot 8^2} = 8\sqrt{2} \, \text{см};$$

Треугольники $PBE$ и $KMD$ равнобедренные и прямоугольные, значит:

$$\angle BHE = \angle DH_1M = 90^\circ, \text{то есть } HH_1 \text{ — высота трапеции};$$

Площадь искомой трапеции:

$$S(x) = \frac{1}{2} HH_1 \cdot (PE + KM) = \frac{1}{2} \left( 8\sqrt{2} — \frac{3\sqrt{2}}{2} — \frac{x\sqrt{2}}{2} \right) (3\sqrt{2} + x\sqrt{2});$$ $$S(x) = \frac{1}{2} \cdot \sqrt{2} \cdot \sqrt{2} \cdot \left( 24 + 8x — \frac{9}{2} — \frac{3x}{2} — \frac{3x}{2} — \frac{x^2}{2} \right) = 19,5 + 5x — \frac{x^2}{2};$$

Производная функции:

$$S'(x) = (19,5 + 5x)’ — \frac{1}{2}(x^2)’ = 5 — \frac{1}{2} \cdot 2x = 5 — x;$$

Промежуток возрастания:

$$5 — x \geq 0, \text{ отсюда } x \leq 5;$$

Наибольшее значение:

$$S(5) = 19,5 + 5 \cdot 5 — \frac{25}{2} = 19,5 + 25 — 12,5 = 32 \, \text{см}^2;$$

Ответ: $32 \, \text{см}^2$.

Отобразим условие задачи:

Дано: Квадрат $ABCD$ с длиной стороны $AB = BC = CD = AD = 8 \, \text{см}$. На сторонах $AB$ и $BC$ взяты точки $P$ и $E$ соответственно так, что $BP = BE = 3 \, \text{см}$. На сторонах $AD$ и $DC$ расположены точки $K$ и $M$ соответственно, так что четырёхугольник $KREM$ является трапецией.

Найти: максимальную площадь трапеции $KREM$.

Шаг 1: Рассмотрение треугольника $PBE$

Рассмотрим прямоугольный треугольник $PBE$ на стороне квадрата $AB$, где $BP = BE = 3 \, \text{см}$. Это равнобедренный прямоугольный треугольник, так как угол $PBE$ равен 90 градусам. Площадь гипотенузы $PE$ можно найти по теореме Пифагора:

$$PE = \sqrt{PB^2 + BE^2} = \sqrt{3^2 + 3^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2} \, \text{см}.$$

Шаг 2: Свойства трапеции $KREM$

Так как $KREM$ — трапеция, отрезки $PE$ и $KM$ параллельны. Следовательно, углы при этих отрезках $\angle KMD = \angle DKM = 45^\circ$, так как $KM$ и $PE$ параллельны, а угол при $K$ и $M$ будет равен $45^\circ$, так как они образуют прямые углы с квадратом.

Шаг 3: Рассмотрение треугольника $KMD$

Рассмотрим треугольник $KMD$, который также является равнобедренным прямоугольным треугольником. Пусть $MD = KD = x$, тогда длина отрезка $KM$ (гипотенуза) будет равна:

$$KM = \sqrt{KD^2 + MD^2} = \sqrt{x^2 + x^2} = \sqrt{2x^2} = x\sqrt{2}.$$

Шаг 4: Диагональ квадрата $BD$

Теперь рассмотрим диагональ квадрата $BD$. Длина диагонали квадрата, который имеет сторону $8 \, \text{см}$, вычисляется по формуле для диагонали квадрата:

$$BD = \sqrt{8^2 + 8^2} = \sqrt{2 \cdot 8^2} = 8\sqrt{2} \, \text{см}.$$

Диагональ пересекает отрезки $PE$ и $KM$ в точках $H$ и $H_1$, соответственно. Эта диагональ разделяет трапецию на два треугольника. Углы $\angle BHE = 90^\circ$ и $\angle DH_1M = 90^\circ$, что значит, что отрезок $HH_1$ — это высота трапеции.

Шаг 5: Площадь трапеции $KREM$

Площадь трапеции можно найти по формуле:

$$S(x) = \frac{1}{2} \cdot HH_1 \cdot (PE + KM),$$

где $HH_1$ — высота трапеции, а $PE$ и $KM$ — основания трапеции.

Теперь найдем выражение для $HH_1$. Внимательно рассматривая диагональ квадрата, мы можем вычислить разницу между длинами отрезков $HH_1$, которая зависит от $x$, так как это связано с положением точек $K$ и $M$.

Высота $HH_1$ вычисляется как разница между длиной диагонали квадрата и длинами отрезков, которые образуют трапецию. Таким образом, $HH_1$ можно выразить как:

$$HH_1 = 8\sqrt{2} — \frac{3\sqrt{2}}{2} — \frac{x\sqrt{2}}{2}.$$

Теперь найдем выражение для площади трапеции:

$$S(x) = \frac{1}{2} \left( 8\sqrt{2} — \frac{3\sqrt{2}}{2} — \frac{x\sqrt{2}}{2} \right) (3\sqrt{2} + x\sqrt{2}).$$

Упростим это выражение:

$$S(x) = \frac{1}{2} \cdot \sqrt{2} \cdot \sqrt{2} \cdot \left( 24 + 8x — \frac{9}{2} — \frac{3x}{2} — \frac{3x}{2} — \frac{x^2}{2} \right),$$ $$S(x) = 19,5 + 5x — \frac{x^2}{2}.$$

Шаг 6: Нахождение максимума площади

Теперь найдем максимальную площадь, найдя производную функции площади $S(x)$. Для этого вычислим производную $S'(x)$:

$$S'(x) = \frac{d}{dx} \left( 19,5 + 5x — \frac{x^2}{2} \right) = 5 — x.$$

Для нахождения критических точек приравняем производную к нулю:

$$5 — x = 0 \implies x = 5.$$

Теперь подставим $x = 5$ в выражение для площади:

$$S(5) = 19,5 + 5 \cdot 5 — \frac{25}{2} = 19,5 + 25 — 12,5 = 32 \, \text{см}^2.$$

Шаг 7: Ответ

Таким образом, наибольшая площадь трапеции $KREM$ равна $32 \, \text{см}^2$.

Ответ: $32 \, \text{см}^2$.