ГДЗ по Алгебре 10 Класс Номер 46.57 Профильный Уровень Мордкович — Подробные Ответы

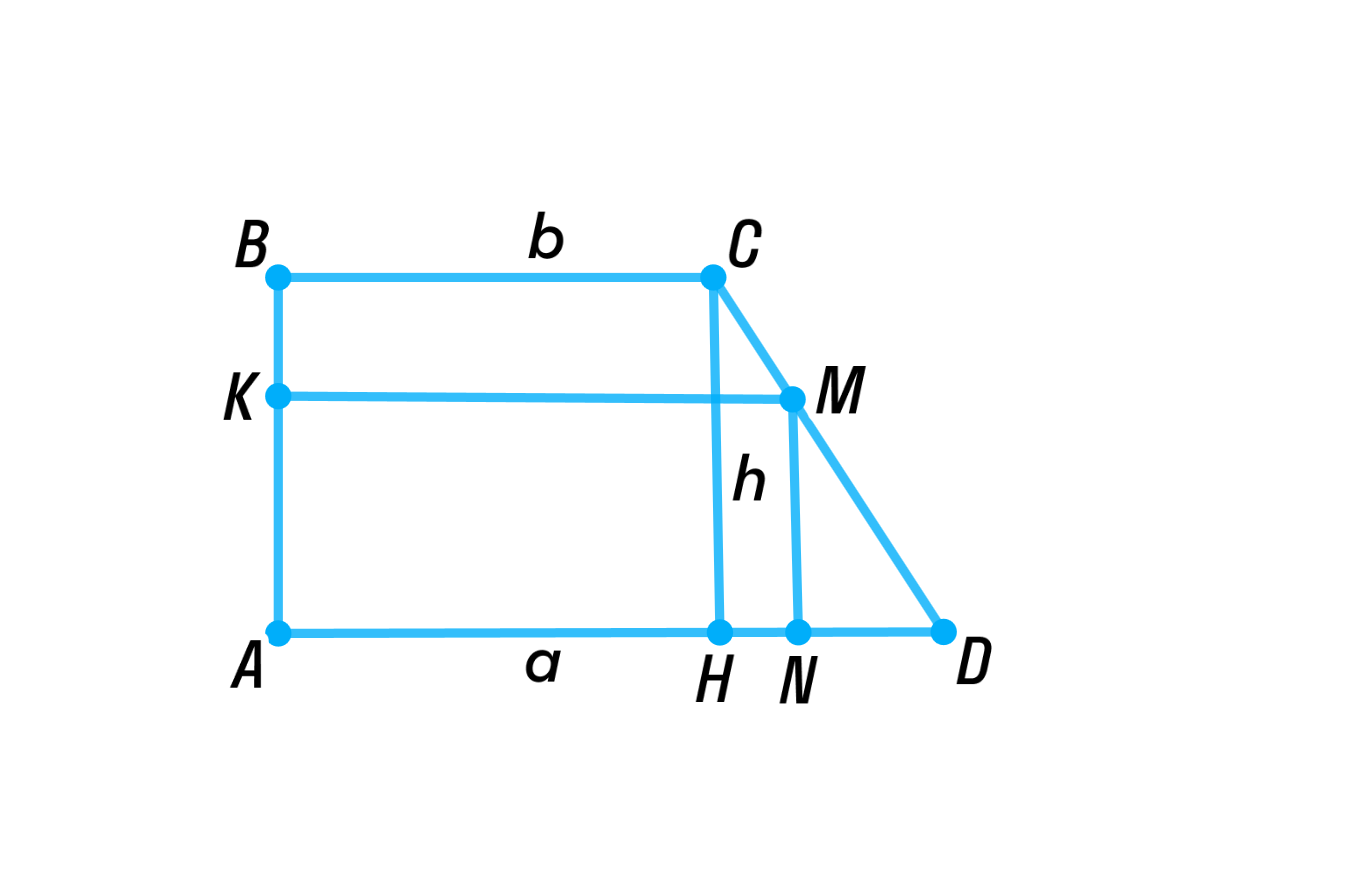
Из прямоугольной трапеции с основаниями $a$ и $b$ и высотой $h$ вырезают прямоугольник наибольшей площади. Чему равна эта площадь, если:

а) $a = 80$, $b = 60$, $h = 100$;

б) $a = 24$, $b = 8$, $h = 12$?

Отобразим условие задачи:

Дано: $ABCD$ — прямоугольная трапеция; $AB = h$; $AD = a$; $BC = b$;

Найти: наибольшую площадь вырезанного прямоугольника;

Решение:

Опустим высоту $CH$ данной трапеции, тогда:
$CH = AB = h;$

Четырехугольник $ABCH$ является прямоугольником, значит:
$AH = BC = b;$
$HD = AD — AH = a — b;$

Пусть точки $A,\ E \in AD,\ F \in CD$ и $M \in AB$ — вершины искомого прямоугольника, при этом $AE = x$, тогда:
$ED = AD — AE = a — x;$

Прямоугольные $\Delta CHD \sim \Delta FED$ по общему острому углу $D$, значит:
$\frac{ED}{HD} = \frac{FE}{CH}, \text{ отсюда } FE = \frac{ED \cdot CH}{HD} = \frac{(a — x) \cdot h}{a — b} = \frac{ah — xh}{a — b};$

Площадь прямоугольника $AMFE$:
$S(x) = AE \cdot FE = x \cdot \frac{ah — xh}{a — b} = \frac{ahx — hx^2}{a — b};$

Производная функции:
$S'(x) = \frac{1}{a — b} \cdot (ah(x)’ — h(x^2)’) = \frac{ah — 2hx}{a — b};$

Промежуток возрастания:

$$\frac{ah — 2hx}{a — b} \geq 0;$$ $$ah — 2hx \geq 0;$$ $$h(a — 2x) \geq 0;$$ $$a — 2x \geq 0;$$ $$a \geq 2x, \text{ отсюда } x \leq \frac{a}{2};$$

Наибольшее значение функции составляет:

$$S\left(\frac{a}{2}\right) = \left(ah \cdot \frac{a}{2} — h \cdot \frac{a^2}{4}\right) : (a — b) = \left(\frac{a^2h}{2} — \frac{a^2h}{4}\right) : (a — b) = \frac{\frac{a^2h}{4}}{a — b} = \frac{a^2h}{4(a — b)};$$

Но если $\frac{a}{2} < b$, тогда наибольшее значение функции равно:

$$S(b) = \frac{ahb — hb^2}{a — b} = \frac{hb(a — b)}{a — b} = hb;$$

а) Если $a = 80$, $b = 60$ и $h = 100$:

$$\frac{a}{2} = \frac{80}{2} = 40 < 60;$$ $$S(60) = 100 \cdot 60 = 6000;$$

б) Если $a = 24$, $b = 8$ и $h = 12$:

$$\frac{a}{2} = \frac{24}{2} = 12 > 8;$$ $$S\left(\frac{a}{2}\right) = \frac{24^2 \cdot 12}{4 \cdot 24 — 4 \cdot 8} = \frac{576 \cdot 12}{96 — 32} = \frac{6912}{64} = 108;$$

Ответ: а) 6000; б) 108.

Дано: $ABCD$ — прямоугольная трапеция; $AB = h$; $AD = a$; $BC = b$.

Необходимо найти: наибольшую площадь вырезанного прямоугольника.

Шаг 1: Определение высоты трапеции

Опустим высоту $CH$ из вершины $C$ трапеции $ABCD$, которая будет перпендикулярна основанию $AB$. Поскольку трапеция прямоугольная, то основание $AB$ является горизонтальным, и высота трапеции $CH$ будет равна высоте $AB$, т.е.:

$$CH = AB = h$$

Это важное замечание, так как высота трапеции будет играть роль в дальнейшем вычислении.

Шаг 2: Геометрия трапеции и прямоугольника

Теперь, зная, что $AB = h$ и что высота $CH = h$, выделим прямоугольник $ABCH$. Этот прямоугольник имеет одну сторону $AB = h$, а вторую сторону $BC = b$. Поэтому:

$$AH = BC = b$$

Кроме того, третья сторона трапеции $AD = a$, а четвертая сторона $HD = AD — AH = a — b$.

Шаг 3: Введение переменной $x$ для ширины прямоугольника

Обозначим переменную $x$ как длину отрезка $AE$, где $E$ — точка на отрезке $AD$, которая будет одной из вершин вырезаемого прямоугольника.

Поскольку точка $A$ на отрезке $AD$, то длина оставшегося отрезка $ED$ равна:

$$ED = AD — AE = a — x$$

Шаг 4: Прямоугольные треугольники и пропорциональность

Теперь рассмотрим два прямоугольных треугольника: $\Delta CHD$ и $\Delta FED$, которые являются подобными. Эти треугольники подобны по общему острому углу $D$.

Для подобных треугольников выполняется пропорциональность соответствующих сторон:

$$\frac{ED}{HD} = \frac{FE}{CH}$$

Из этой пропорции мы можем выразить длину $FE$ — одной из сторон вырезаемого прямоугольника:

$$FE = \frac{ED \cdot CH}{HD} = \frac{(a — x) \cdot h}{a — b}$$

Теперь подставим $ED = a — x$ и $HD = a — b$, получаем:

$$FE = \frac{(a — x) \cdot h}{a — b}$$

Шаг 5: Площадь прямоугольника

Площадь прямоугольника $AMFE$ будет равна произведению его сторон:

$$S(x) = AE \cdot FE = x \cdot \frac{(a — x) \cdot h}{a — b}$$

Раскроем скобки:

$$S(x) = \frac{h \cdot x \cdot (a — x)}{a — b} = \frac{h \cdot (ax — x^2)}{a — b}$$

Это — функция площади прямоугольника $S(x)$ от переменной $x$.

Шаг 6: Нахождение производной

Для нахождения максимума площади, нужно найти производную функции площади $S(x)$ и приравнять её к нулю.

Вычислим производную $S'(x)$:

$$S'(x) = \frac{d}{dx} \left( \frac{h \cdot (ax — x^2)}{a — b} \right)$$

Так как $a — b$ — это константа, она выносится за знак производной:

$$S'(x) = \frac{h}{a — b} \cdot \frac{d}{dx} (ax — x^2)$$

Теперь находим производную от $ax — x^2$:

$$\frac{d}{dx} (ax — x^2) = a — 2x$$

Таким образом:

$$S'(x) = \frac{h \cdot (a — 2x)}{a — b}$$

Шаг 7: Нахождение критической точки

Для нахождения максимума функции площади, приравняем производную $S'(x)$ к нулю:

$$\frac{h \cdot (a — 2x)}{a — b} = 0$$

Так как $h \neq 0$ и $a — b \neq 0$, остаётся:

$$a — 2x = 0$$

Отсюда:

$$x = \frac{a}{2}$$

Шаг 8: Наибольшее значение функции

Теперь подставим $x = \frac{a}{2}$ в функцию площади, чтобы найти максимальную площадь:

$$S\left(\frac{a}{2}\right) = \frac{h \cdot \left(a \cdot \frac{a}{2} — \left(\frac{a}{2}\right)^2\right)}{a — b}$$

Выполним вычисления:

$$S\left(\frac{a}{2}\right) = \frac{h \cdot \left(\frac{a^2}{2} — \frac{a^2}{4}\right)}{a — b}$$ $$S\left(\frac{a}{2}\right) = \frac{h \cdot \frac{a^2}{4}}{a — b}$$

Итак, наибольшая площадь прямоугольника при $x = \frac{a}{2}$ равна:

$$S_{\text{max}} = \frac{a^2 h}{4(a — b)}$$

Шаг 9: Условие для выбора максимальной площади

Однако, существует ещё одно условие: если $\frac{a}{2} < b$, то максимальная площадь будет достигаться при $x = b$, и площадь будет равна:

$$S(b) = \frac{h \cdot b \cdot (a — b)}{a — b} = h \cdot b$$

Применение для конкретных значений

а) $a = 80$, $b = 60$, $h = 100$

Мы знаем, что:

$$\frac{a}{2} = \frac{80}{2} = 40 < 60$$

Так как $\frac{a}{2} < b$, то максимальная площадь будет равна:

$$S_{\text{max}} = h \cdot b = 100 \cdot 60 = 6000$$

б) $a = 24$, $b = 8$, $h = 12$

Здесь:

$$\frac{a}{2} = \frac{24}{2} = 12 > 8$$

Так как $\frac{a}{2} > b$, то максимальная площадь будет равна:

$$S_{\text{max}} = \frac{a^2 h}{4(a — b)} = \frac{24^2 \cdot 12}{4(24 — 8)} = \frac{576 \cdot 12}{64} = 108$$