ГДЗ по Алгебре 10 Класс Номер 46.58 Профильный Уровень Мордкович — Подробные Ответы

У пятиугольника $ABCDE$ углы $A$, $B$ и $E$ — прямые, $AB = a$, $BC = b$, $AE = c$, $DE = m$. Впишите в пятиугольник прямоугольник наибольшей площади, если:

а) $a = 7$, $b = 9$, $c = 3$, $m = 5$;

б) $a = 7$, $b = 18$, $c = 3$, $m = 1$.

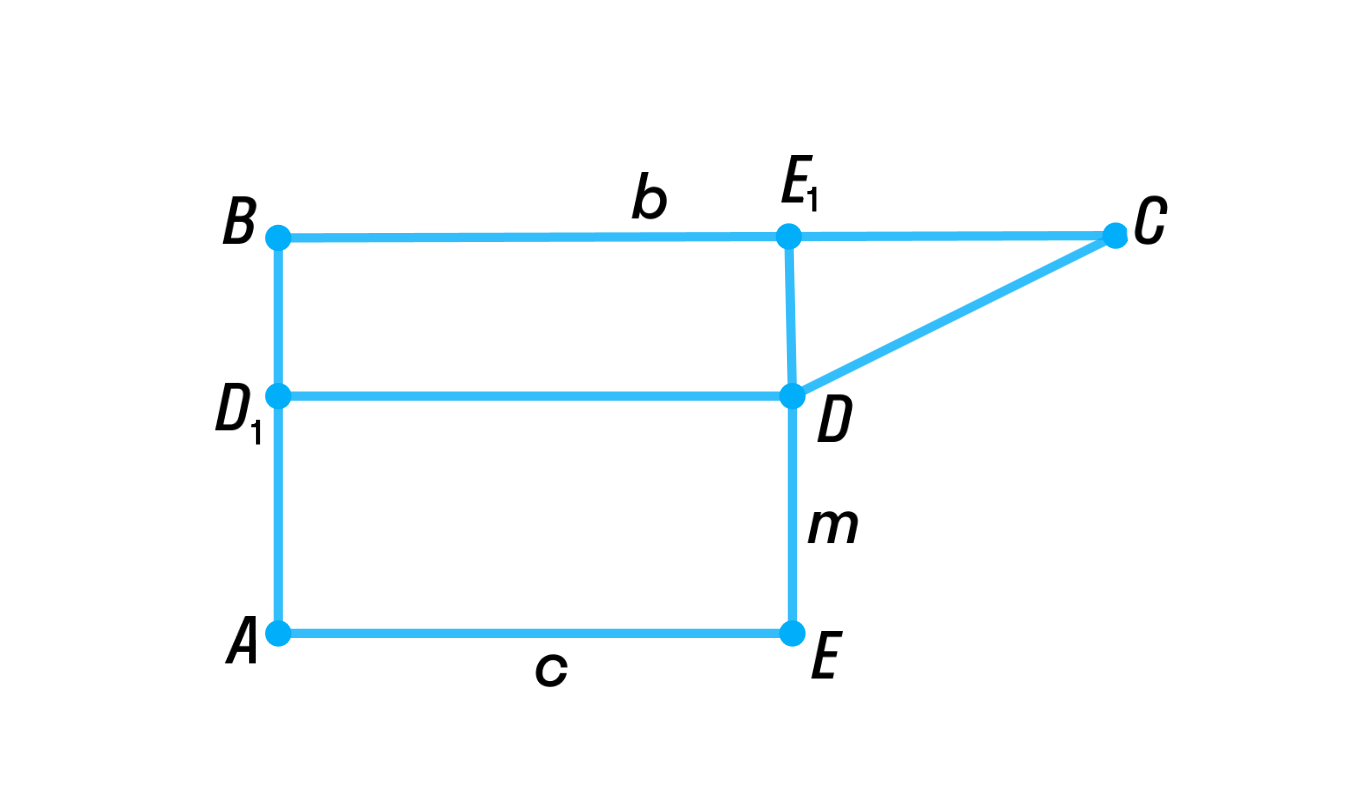
Отобразим условие задачи:

Дано: пятиугольник $ABCDE$; $\angle A = \angle B = \angle E = 90^\circ$; $AB = a$; $BC = b$; $AE = c$; $DE = m$;

Найти: прямоугольник с наибольшей площадью;

Решение:

1. Опустим перпендикуляры $DE_1$ на сторону $BC$ и $DD_1$ на сторону $AB$;
2. Наибольшую площадь имеет либо прямоугольник $ABE_1E$, либо прямоугольник, вписанный в прямоугольную трапецию $BD_1DC$;
3. Площадь прямоугольника $ABE_1E$ равна:
   $S_{ABE_1E} = AB \cdot BE = a \cdot c;$
4. Площадь трапеции $B_1D_1DC$ равна:
   $S_{B_1D_1DC} = \frac{1}{2} DE_1 \cdot (BC + DD_1) = \frac{1}{2} (AB — DE)(BC + AE) = \frac{1}{2}(a — m)(b + c);$
5. Во втором случае воспользуемся формулой, полученной в задаче 46.57:
   $S\left(\frac{b}{2}\right) = \frac{b^2 \cdot (a — m)}{4b — 4c};$

а) Если $a = 7$, $b = 9$, $c = 3$ и $m = 5$:

$S_{ABE_1E} = 7 \cdot 3 = 21;$
$S_{BD_1DC} = \frac{1}{2}(7 — 5)(9 + 3) = \frac{1}{2} \cdot 2 \cdot 12 = 12;$
$S_{ABE_1E} > S_{BD_1DC}, \text{значит } S_{\text{max}} = 21;$

б) Если $a = 7$, $b = 18$, $c = 3$ и $m = 1$:

$S_{ABE_1E} = 7 \cdot 3 = 21;$
$S_{BD_1DC} = \frac{1}{2}(7 — 1)(18 + 3) = \frac{1}{2} \cdot 6 \cdot 21 = 63;$
$S_{BD_1DC} > S_{ABE_1E} \text{ и } \frac{b}{2} = \frac{18}{2} = 9 > c \text{ значит:}$
$S_{\text{max}} = \frac{18^2 \cdot (7 — 1)}{4 \cdot 18 — 4 \cdot 3} = \frac{324 \cdot 6}{72 — 12} = \frac{1944}{60} = 32,4;$

Ответ: а) 21; б) 32,4.

Дано: пятиугольник $ABCDE$, в котором углы $\angle A = \angle B = \angle E = 90^\circ$, стороны $AB = a$, $BC = b$, $AE = c$, $DE = m$.

Необходимо найти прямоугольник с наибольшей площадью, вписанный в данный пятиугольник.

Решение:

1. Определение геометрической фигуры

Данный пятиугольник состоит из двух прямых углов (в точках $A$ и $B$) и одного прямого угла в точке $E$. Мы будем искать прямоугольник наибольшей площади, который можно вписать в этот пятиугольник.

Обозначим вершины пятиугольника следующим образом:

• $A$ — точка, где угол $A$ прямой.
• $B$ — точка, где угол $B$ прямой.
• $E$ — точка, где угол $E$ прямой.
• $C$ и $D$ — точки на сторонах $BC$ и $DE$, соответственно.

2. Строим вспомогательные элементы

Для поиска наибольшего прямоугольника мы будем использовать несколько вспомогательных перпендикуляров, которые позволят нам разделить фигуру на более простые элементы, с помощью которых можно будет вычислить площадь.

Шаг 1: Опустим перпендикуляр $DE_1$ с точки $D$ на сторону $BC$, а также перпендикуляр $DD_1$ с точки $D$ на сторону $AB$.

Эти перпендикуляры помогут нам разбить фигуру на прямоугольники и трапеции, что упростит нахождение максимальной площади.

Шаг 2: Наибольшую площадь может иметь либо прямоугольник $ABE_1E$, либо прямоугольник, вписанный в прямоугольную трапецию $BD_1DC$.

Теперь вычислим площадь этих двух фигур и сравним их.

3. Вычисление площади прямоугольника $ABE_1E$

Площадь прямоугольника $ABE_1E$ равна произведению его сторон. Одна сторона этого прямоугольника — это сторона $AB = a$, а другая сторона — это длина отрезка $BE = c$.

Таким образом, площадь прямоугольника $ABE_1E$ можно выразить как:

$$S_{ABE_1E} = AB \cdot BE = a \cdot c$$

4. Вычисление площади трапеции $BD_1DC$

Площадь трапеции $BD_1DC$ можно вычислить по формуле площади трапеции, которая имеет вид:

$$S_{\text{трапеции}} = \frac{1}{2} \cdot (основание_1 + основание_2) \cdot высота$$

В нашем случае основания трапеции — это отрезки $DE_1$ и $DD_1$, а высотой является расстояние между основаниями, которое равно сумме $BC + AE = b + c$.

Таким образом, площадь трапеции можно выразить как:

$$S_{B_1D_1DC} = \frac{1}{2} \cdot (AB — DE) \cdot (BC + AE)$$ $$S_{B_1D_1DC} = \frac{1}{2} \cdot (a — m) \cdot (b + c)$$

5. Применение формулы для прямоугольника, вписанного в трапецию

Для второго случая, когда наибольшая площадь будет у прямоугольника, вписанного в трапецию $BD_1DC$, мы воспользуемся формулой, полученной в задаче 46.57. Эта формула позволяет вычислить площадь прямоугольника, вписанного в трапецию с основанием $b$, высотой $c$ и параметром $m$, при котором достигается максимальная площадь.

Формула имеет вид:

$$S\left( \frac{b}{2} \right) = \frac{b^2 \cdot (a — m)}{4b — 4c}$$

6. Подставляем значения и вычисляем для каждого случая

а) Когда $a = 7$, $b = 9$, $c = 3$ и $m = 5$:

Площадь прямоугольника $ABE_1E$:

$$S_{ABE_1E} = 7 \cdot 3 = 21$$

Площадь трапеции $BD_1DC$:

$$S_{BD_1DC} = \frac{1}{2} \cdot (7 — 5) \cdot (9 + 3) = \frac{1}{2} \cdot 2 \cdot 12 = 12$$

Сравниваем площади:

$$S_{ABE_1E} = 21, \quad S_{BD_1DC} = 12$$

Так как $S_{ABE_1E} > S_{BD_1DC}$, максимальная площадь в этом случае равна $S_{\text{max}} = 21$.

б) Когда $a = 7$, $b = 18$, $c = 3$ и $m = 1$:

Площадь прямоугольника $ABE_1E$:

$$S_{ABE_1E} = 7 \cdot 3 = 21$$

Площадь трапеции $BD_1DC$:

$$S_{BD_1DC} = \frac{1}{2} \cdot (7 — 1) \cdot (18 + 3) = \frac{1}{2} \cdot 6 \cdot 21 = 63$$

Сравниваем площади:

$$S_{ABE_1E} = 21, \quad S_{BD_1DC} = 63$$

Так как $S_{BD_1DC} > S_{ABE_1E}$, теперь используем формулу для прямоугольника, вписанного в трапецию:

$$S_{\text{max}} = \frac{18^2 \cdot (7 — 1)}{4 \cdot 18 — 4 \cdot 3}$$ $$S_{\text{max}} = \frac{324 \cdot 6}{72 — 12} = \frac{1944}{60} = 32,4$$

Ответ:

а) 21

б) 32,4