ГДЗ по Алгебре 10 Класс Номер 46.59 Профильный Уровень Мордкович — Подробные Ответы

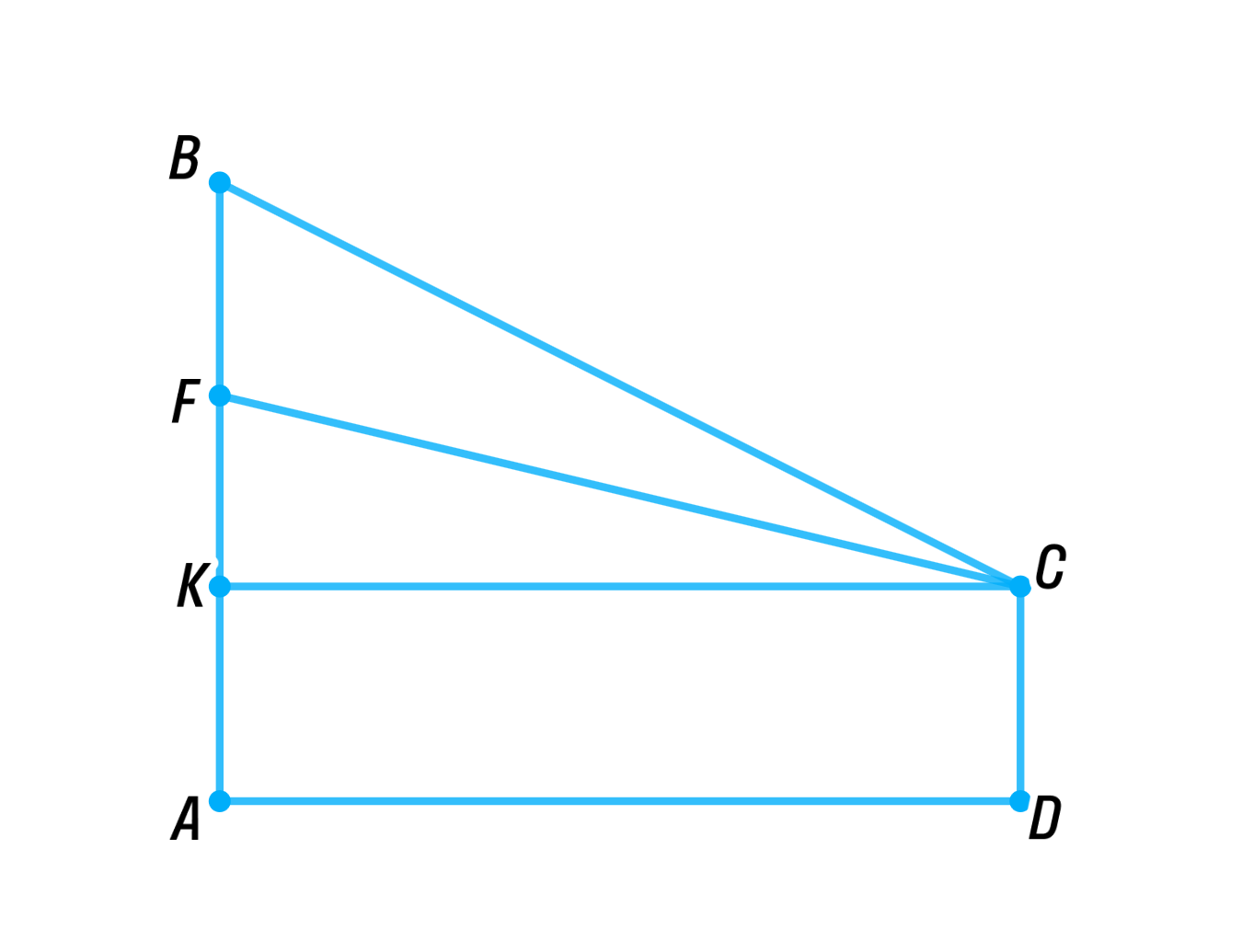
Памятник состоит из статуи и постамента. К памятнику подошёл человек. Верхняя точка памятника находится выше уровня глаз человека на $a$ м, а верхняя точка постамента — на $b$ м. На каком расстоянии от памятника должен стать человек, чтобы видеть статую под наибольшим углом?

Отобразим условие задачи:

Решение:

Пусть $x$ — искомое расстояние между человеком и статуей, отрезок $AB$ — сама статуя и точка $C$ — глаза человека;

Опустим перпендикуляр $CH$ на прямую $AB$, тогда:

$$CH = x, \quad AH = a \quad \text{и} \quad BH = b;$$ $$\operatorname{tg} \angle BCH = \frac{BH}{CH} = \frac{b}{x};$$ $$\operatorname{tg} \angle ACH = \frac{AH}{CH} = \frac{a}{x};$$

Пусть тангенс угла $ACB$ равен $z$, тогда:

$$\operatorname{tg} \angle ACH = \operatorname{tg} (\angle ACB + \angle BCH) = \frac{\operatorname{tg} \angle ACB + \operatorname{tg} \angle BCH}{1 — \operatorname{tg} \angle ACH \cdot \operatorname{tg} \angle BCH};$$ $$\operatorname{tg} \angle ACH = \frac{z + \frac{b}{x}}{1 — z \cdot \frac{b}{x}} = \frac{b + zx}{x(1 — zb)} = \frac{b + zx}{x — zb};$$

Получаем уравнение:

$$\frac{b + zx}{x — zb} = \frac{a}{x};$$ $$x(b + zx) = a(x — zb);$$ $$xb + zx^2 = ax — azb;$$ $$zx^2 + azb = ax — xb;$$ $$z(x^2 + ab) = x(a — b);$$ $$z = \frac{x(a — b)}{x^2 + ab};$$

Производная функции:

$$z'(x) = \frac{(a — b)(x)'(x^2 + ab) — x(a — b)(x^2 + ab)’}{(x^2 + ab)^2};$$ $$z'(x) = \frac{(a — b)(x^2 + ab) — x(a — b) \cdot 2x}{(x^2 + ab)^2};$$ $$z'(x) = \frac{(a — b)(x^2 + ab — 2x^2)}{(x^2 + ab)^2} = \frac{(a — b)(ab — x^2)}{(x^2 + ab)^2};$$

Промежуток возрастания:

$$\frac{(a — b)(ab — x^2)}{(x^2 + ab)^2} \geq 0;$$ $$ab — x^2 \geq 0;$$ $$ab \geq x^2;$$ $$-\sqrt{ab} \leq x \leq \sqrt{ab};$$

Точка максимума: $x = \sqrt{ab}$;

Ответ: $\sqrt{ab}$.

Задача:
Памятник состоит из статуи и постамента. Человек подошёл к памятнику так, что верхняя точка памятника находится выше уровня его глаз на $a$ метров, а верхняя точка постамента — на $b$ метров. Нужно найти, на каком расстоянии от памятника человек должен стать, чтобы увидеть статую под наибольшим углом.

Решение:

1. Пусть $x$ — это расстояние между человеком и статуей (то есть искомое расстояние).
2. Точка $A$ — верхняя точка памятника, $B$ — верхняя точка постамента, а $C$ — глаза человека.
3. Опустим перпендикуляр $CH$ на прямую $AB$, где $H$ — это точка пересечения перпендикуляра с прямой $AB$.
4. Тогда:
   • $AH = a$ — высота памятника.
   • $BH = b$ — высота постамента.
   • $CH = x$ — расстояние между человеком и памятником.

Мы будем искать максимальный угол $\angle ACB$, который человек видит, смотря на статую.

Шаг 1: Углы и тангенсы

1. Тангенс угла $\angle BCH$ (угол между линией зрения человека к точке $B$ и горизонтом):

   $$\operatorname{tg} \angle BCH = \frac{BH}{CH} = \frac{b}{x}.$$

2. Тангенс угла $\angle ACH$ (угол между линией зрения человека к точке $A$ и горизонтом):

   $$\operatorname{tg} \angle ACH = \frac{AH}{CH} = \frac{a}{x}.$$

Шаг 2: Угол между линиями

Для нахождения угла $\angle ACB$ между двумя линиями $AC$ и $BC$, используем формулу для тангенса угла между двумя прямыми:

$$\operatorname{tg} \angle ACB = \frac{\operatorname{tg} \angle ACH + \operatorname{tg} \angle BCH}{1 — \operatorname{tg} \angle ACH \cdot \operatorname{tg} \angle BCH}.$$

Подставляем выражения для тангенсов:

$$\operatorname{tg} \angle ACB = \frac{\frac{a}{x} + \frac{b}{x}}{1 — \frac{a}{x} \cdot \frac{b}{x}} = \frac{\frac{a + b}{x}}{1 — \frac{ab}{x^2}}.$$

Упростим:

$$\operatorname{tg} \angle ACB = \frac{a + b}{x — \frac{ab}{x}} = \frac{(a + b)x}{x^2 — ab}.$$

Шаг 3: Максимизация функции тангенса

Теперь необходимо найти значение $x$, при котором функция $\operatorname{tg} \angle ACB$ будет максимальной. Для этого вычислим производную функции по $x$ и приравняем её к нулю.

Производная от $\frac{(a + b)x}{x^2 — ab}$ по $x$ — это:

$$\frac{d}{dx} \left( \frac{(a + b)x}{x^2 — ab} \right) = \frac{(x^2 — ab)(a + b) — (a + b)x \cdot 2x}{(x^2 — ab)^2}.$$

Упростим числитель:

$$= \frac{(a + b)(x^2 — ab) — 2x^2(a + b)}{(x^2 — ab)^2} = \frac{(a + b)(-x^2 — ab)}{(x^2 — ab)^2}.$$

Чтобы найти максимальное значение, приравняем производную к нулю:

$$(a + b)(-x^2 — ab) = 0.$$

Решение этого уравнения даёт:

$$x^2 + ab = 0.$$

Так как $x^2 \geq 0$ и $ab \geq 0$, это означает, что $x = \sqrt{ab}$.

Ответ:

Человек должен стоять на расстоянии $\sqrt{ab}$ от памятника, чтобы видеть статую под наибольшим углом.

Ответ: $x = \sqrt{ab}$.