ГДЗ по Алгебре 10 Класс Номер 47.8 Профильный Уровень Мордкович — Подробные Ответы

Ученик помнит, что в формуле азотной кислоты подряд идут буквы Н, N, О и что есть один нижний индекс — то ли двойка, то ли тройка.

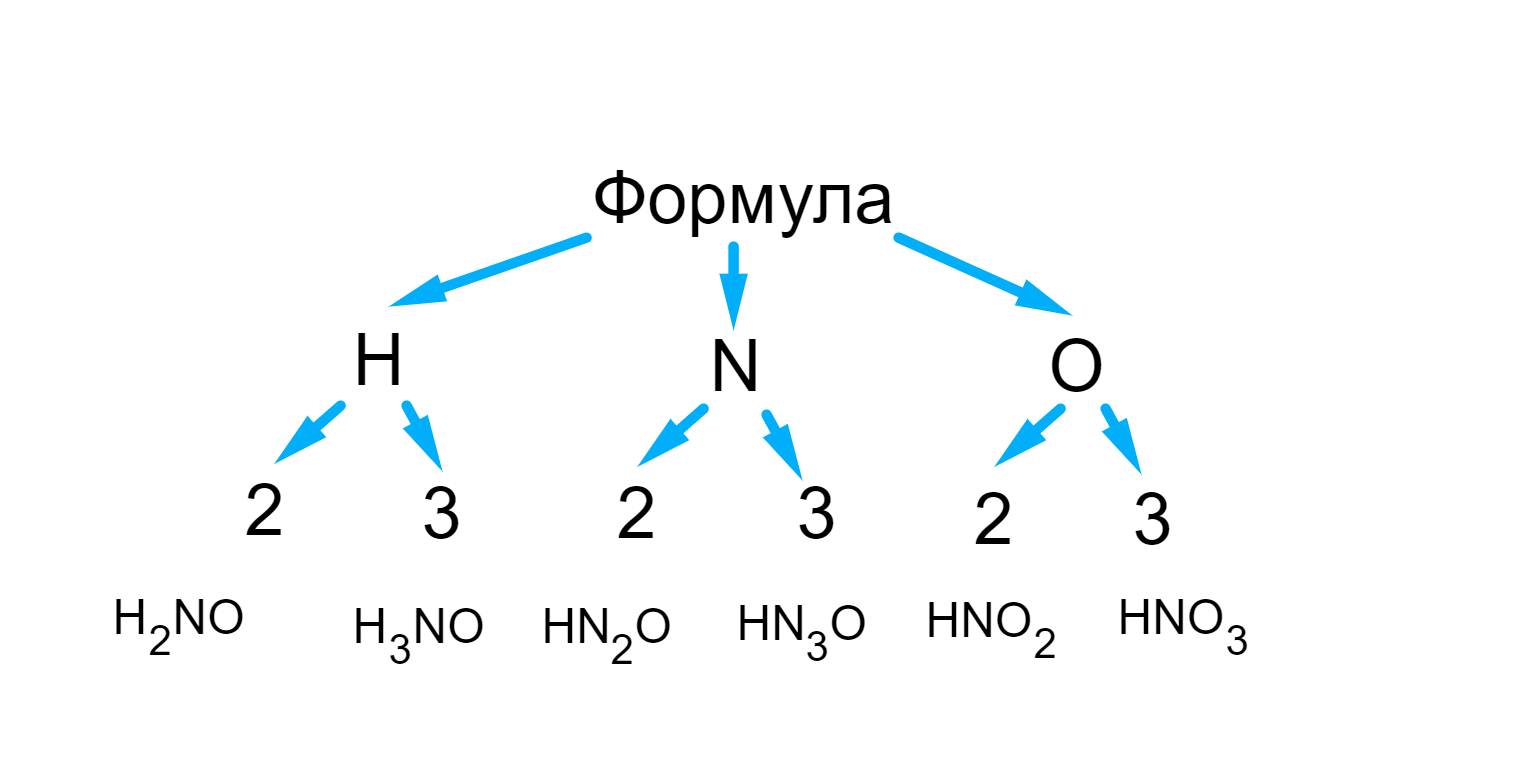
a) Нарисуйте дерево возможных вариантов, из которых ученику придется выбирать ответ.

б) Сколько среди них тех, в которых индекс стоит не втором месте?

в) Как изменится дерево вариантов, если ученик помнит что на первом месте точно стоит Я, а порядок остальных букв забыл?

г) Как изменится дерево вариантов, если буквы могут идти в любом порядке?

Формула азотной кислоты состоит из букв $HNO$ и одного из нижних индексов 2 или 3;

а) Дерево всех возможных вариантов формулы:

б) Индекс стоит не на втором месте в четырех вариантах:
$N = \{HN2O; HN3O; HNO2; HNO3\} = 4;$

в) Если ученик помнит только, что на первом месте стоит $H$, но порядок остальных букв забыл, то появится еще две ветви — одна для буквы $O$, стоящей на втором месте и одна для буквы $N$, стоящей на третьем месте, тогда число вариантов увеличится на $N = 2 \cdot 2 = 4$;

г) Если все буквы могут идти в любом порядке, то данное дерево вариантов увеличится в $P_3 = 3 \cdot 2 = 6$ раз;

Необходимо рассмотреть все возможные варианты формулы азотной кислоты. Формула состоит из букв $H$, $N$ и $O$, причем один из индексов (после $N$ или $O$) может быть 2 или 3.

Шаг 1: Дерево всех возможных вариантов формулы

а) Дерево всех возможных вариантов формулы:

В начале мы имеем 3 буквы: $H$, $N$, $O$. К каждой из них могут быть добавлены индексы $2$ или $3$. Поскольку $H$ всегда стоит на первом месте, рассматриваем только варианты для букв $N$ и $O$. У нас могут быть следующие варианты:

• $HN_2O_2$
• $HN_2O_3$
• $HN_3O_2$
• $HN_3O_3$
• $HNO_2$
• $HNO_3$

В общем случае, дерево вариантов будет включать такие ветви, где для $N$ и $O$ стоят индексы $2$ или $3$. Итого, для каждой из букв $N$ и $O$ мы имеем по 2 варианта, что дает 4 возможных комбинации.

Шаг 2: Индекс не на втором месте

б) Индекс стоит не на втором месте в четырех вариантах:

Первые варианты — это те, где индекс не стоит на втором месте, то есть:

1. $HN_2O_2$
2. $HN_2O_3$
3. $HN_3O_2$
4. $HN_3O_3$

Итак, мы видим, что индекс стоит не на втором месте в четырех вариантах. Это те варианты, где индексы размещаются только на местах после $N$ и $O$. В этих вариантах индексы находятся в позициях, которые не изменяют основной порядок (то есть индекс $2$ или $3$ не ставится на второй букве, и они остаются после $N$ или $O$).

Шаг 3: Порядок букв на 2-3 позиции

в) Если ученик помнит только, что на первом месте стоит $H$, но порядок остальных букв забыл:

Предположим, что ученик помнит, что на первом месте точно стоит $H$, но не помнит порядок букв $N$ и $O$. В этом случае возможны два расположения букв $N$ и $O$:

• $HNO$ (где на втором месте $N$ и на третьем $O$)
• $HON$ (где на втором месте $O$ и на третьем $N$)

В этом случае появятся новые ветви для каждого из этих расположений. То есть, если мы добавляем индексы $2$ или $3$, то число вариантов увеличивается. Каждый из двух вариантов $HNO$ и $HON$ можно дополнить двумя индексами для каждой из букв $N$ и $O$:

1. Для $HNO$: возможны варианты $HN_2O_2$, $HN_2O_3$, $HN_3O_2$, $HN_3O_3$.
2. Для $HON$: возможны варианты $H_2NO_2$, $H_2NO_3$, $H_3NO_2$, $H_3NO_3$.

Таким образом, мы получаем $2 \times 2 \times 2 = 8$ вариантов (по 4 для каждой из комбинаций). Однако важным моментом является тот факт, что здесь увеличение числа вариантов происходит именно из-за возможности менять порядок букв $N$ и $O$.

Шаг 4: Все буквы могут быть в любом порядке

г) Если все буквы могут идти в любом порядке:

Теперь рассмотрим случай, когда буквы $H$, $N$ и $O$ могут располагаться в любом порядке. Это означает, что мы можем переставлять их местами, получая 6 различных комбинаций, поскольку все буквы различны. Порядок будет следующим:

1. $HNO$
2. $HON$
3. $NHO$
4. $NOH$
5. $OHN$
6. $ONH$

Таким образом, число вариантов увеличится в 6 раз. Для каждой из этих комбинаций мы можем установить индексы $2$ или $3$ для $N$ и $O$. Это увеличивает количество вариантов на $P_3 = 6$ раз.$$6 \times 4 = 24 \text{ варианта}.$$