ГДЗ по Алгебре 10 Класс Номер 47.9 Профильный Уровень Мордкович — Подробные Ответы

В урне лежат три неразличимых на ощупь шара, два белых и один черный. При вытаскивании черного шара его возвращают обратно, а вытащенный белый шар откладывают в сторону. Такую операцию производят два раза подряд.

a) Нарисуйте дерево возможных вариантов.

б) В скольких случаях оба вытащенных шара будут черными?

в) В скольких случаях вытащенные шары будут разного цвета?

г) Нарисуйте дерево возможных вариантов для трех вытаскиваний из двух черных и двух белых шаров.

В урне лежат три шара — два белых и один черный;

При вытаскивании черного шара, его возвращают обратно, а вытащенный белый шар откладывают в сторону, такую операцию проводят два раза;

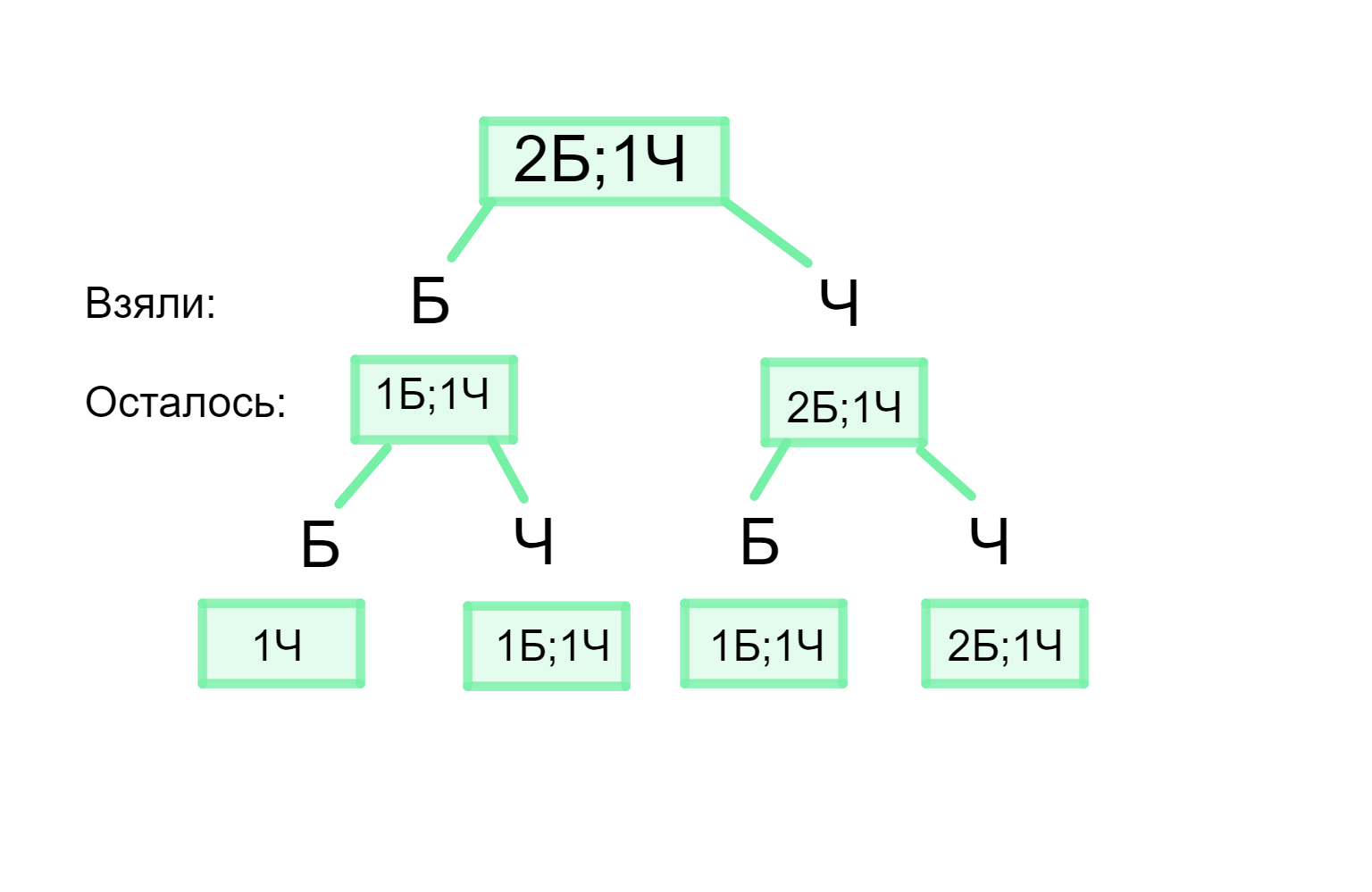
а) Дерево всех возможных вариантов вытаскиваний:

б) Оба вытащенных шара будут черными в одном случае:

$N = \{\text{ЧЧ}\} = 1$;

в) Вытащенные шары будут разного цвета в двух случаях:

$N = \{\text{БЧ; ЧБ}\} = 2$;

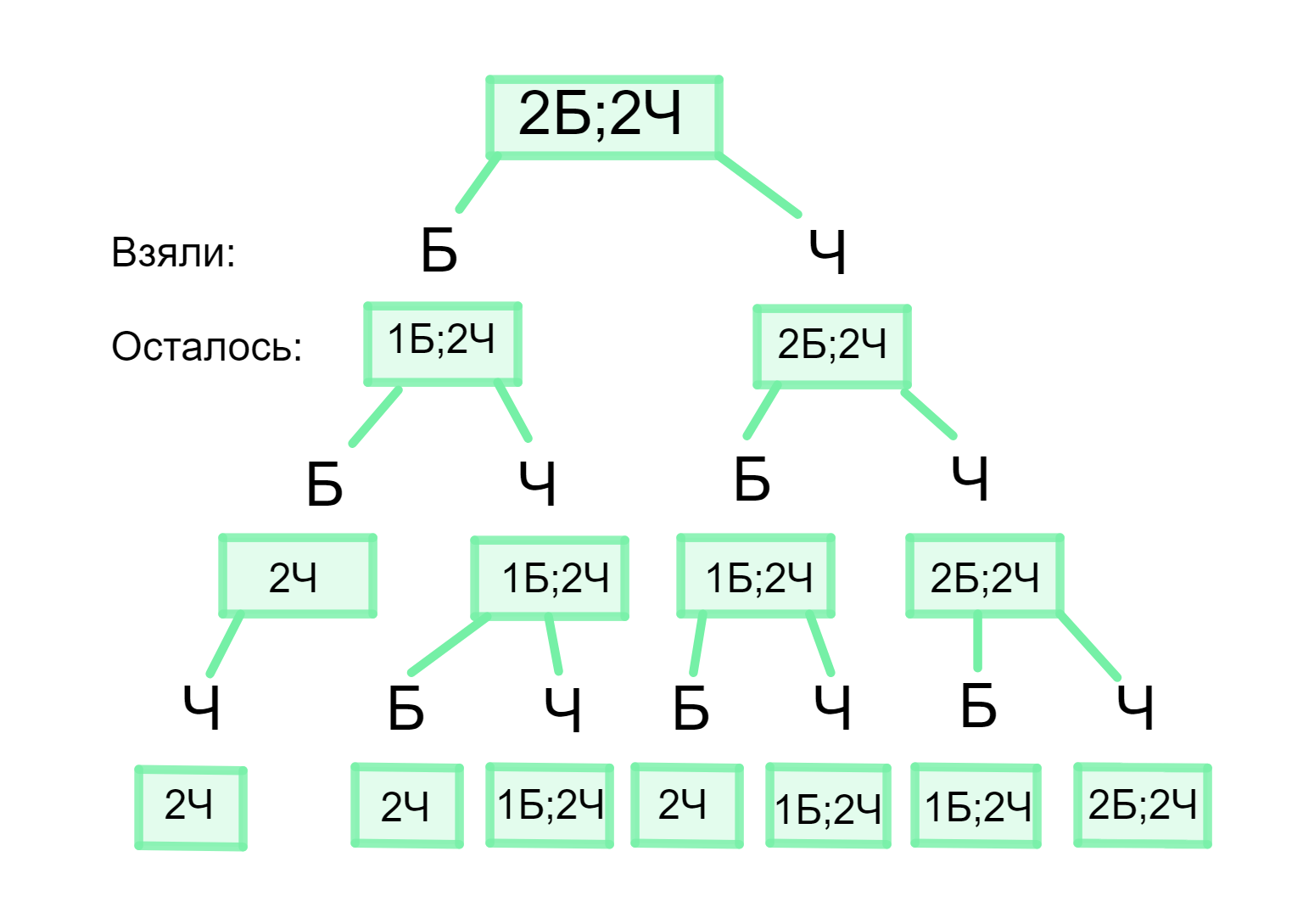
г) Дерево возможных вариантов для трех вытаскиваний из двух черных и двух белых шаров:

Исходные данные:

• В урне три шара: два белых (Б) и один черный (Ч).
• При вытаскивании черного шара его возвращают обратно, а белый шар откладывают в сторону.
• Операцию вытаскивания производят дважды подряд.

а) Дерево возможных вариантов вытаскиваний:

Мы будем рисовать дерево возможных событий для каждого вытаскивания.

1. Первое вытаскивание:

• Возможные результаты:
  • Белый шар (Б)
  • Черный шар (Ч)

2. Второе вытаскивание:

• Если в первом вытаскивании был белый шар (Б), то мы продолжаем вытаскивать из оставшихся двух шаров (один белый и один черный), то есть возможные результаты:
  • Белый шар (Б)
  • Черный шар (Ч)
• Если в первом вытаскивании был черный шар (Ч), то его возвращаем обратно, и снова можно вытащить либо белый (Б), либо черный (Ч).

Таким образом, дерево возможных вариантов выглядит следующим образом:

б) В скольких случаях оба вытащенных шара будут черными?

Рассмотрим все варианты, когда оба вытащенных шара будут черными.

• В первом вытаскивании должен быть вытащен черный шар (Ч).
• Во втором вытаскивании также должен быть вытащен черный шар (Ч).

Только один путь ведет к тому, чтобы оба шара были черными: первый раз — черный (Ч), второй раз — черный (Ч).

Ответ: 1 случай.

в) В скольких случаях вытащенные шары будут разного цвета?

Рассмотрим случаи, когда шары будут разного цвета. Это возможно, если в одном из вытаскиваний будет белый (Б), а в другом — черный (Ч). Мы должны учитывать порядок вытаскивания.

• В первом вытаскивании — белый (Б), во втором — черный (Ч).
• В первом вытаскивании — черный (Ч), во втором — белый (Б).

Таким образом, два варианта, когда вытащенные шары будут разного цвета:

1. Первый белый (Б), второй черный (Ч)
2. Первый черный (Ч), второй белый (Б)

Ответ: 2 случая.

г) Дерево возможных вариантов для трех вытаскиваний из двух черных и двух белых шаров:

Теперь нам нужно рассмотреть ситуацию, когда из урны вытаскивают 3 шара подряд, в урне всего 2 белых и 2 черных шара.

При этом операция извлечения будет без возврата (то есть шары не возвращаются обратно в урну). Возможные варианты выглядят следующим образом:

1. Первое вытаскивание:

• Возможности:
  • Белый шар (Б)
  • Черный шар (Ч)

2. Второе вытаскивание:

• Если в первом вытаскивании был белый шар (Б), то остаются шары: один белый (Б) и один черный (Ч).
• Если в первом вытаскивании был черный шар (Ч), то остаются шары: два белых (Б).

3. Третье вытаскивание:

• После второго вытаскивания остаются разные комбинации оставшихся шаров.

Дерево для этого случая будет выглядеть так:

Итак, дерево для трех вытаскиваний из двух черных и двух белых шаров:

• Первый шаг: Выбираем белый (Б) или черный (Ч).
• Второй шаг: Если был белый, то выбираем из оставшихся белых и черных. Если был черный, то выбираем из оставшихся двух белых.
• Третий шаг: В зависимости от предыдущих выборов, выбираем из оставшихся.