ГДЗ по Алгебре 10 Класс Номер 48.18 Профильный Уровень Мордкович — Подробные Ответы

Пусть $y(n) = \frac{C_n^3}{A_{n-1}^3}, \, n \geqslant 4$.

а) Укажите дробно-линейную функцию, на графике которой лежат все точки $(n; y(n))$.

б) Постройте график этой функции.

в) Укажите наибольшее $n$, при котором $y(n) > 0.25$.

г) Укажите наименьшее $n$, при котором $y(n)$ отличается от $\frac{1}{6}$ менее чем на 0.01.

Пусть $y(n) = \frac{C_n^3}{A_{n-1}^3}$, где $n \geq 4$;

а) Дробно-линейная функция, которой принадлежат точки $(n; y(n))$:

$$y(n) = \frac{n!}{3! \cdot (n-3)!} : \frac{(n-1)!}{(n-1-3)!} = \frac{n(n-1)!}{3! \cdot (n-3)!} \cdot \frac{(n-4)!}{(n-1)!} = \frac{n}{6(n-3)}.$$

Ответ: $y = \frac{x}{6(x-3)}$.

б) График этой функции:

$$x_0 — 3 = 0, \text{ отсюда } x_0 = 3;$$ $$y_0 = \lim_{x \to \infty} \frac{x}{6(x-3)} = \lim_{x \to \infty} \frac{1}{6} \cdot \frac{1}{1 — \frac{3}{x}} = \frac{1}{6} \cdot \frac{1}{1 — 0} = \frac{1}{6}.$$

Таблица значений:

в) Наибольшее число $n$, при котором $y(n) > 0,25$:

$$\frac{n}{6(n-3)} > 0,25;$$ $$n > 1,5(n-3);$$ $$n > 1,5n — 4,5;$$ $$-0,5n > -4,5, \text{ отсюда } n < 9;$$

Ответ: $n = 8$.

г) Наименьшее $n$, при котором $y(n)$ отличается от $\frac{1}{6}$ менее, чем на 0,01:

$$\left| \frac{n}{6(n-3)} — \frac{1}{6} \right| < 0,01;$$ $$\left| \frac{n — n + 3}{6(n-3)} \right| < 0,01;$$ $$\left| \frac{1}{2(n-3)} \right| < \frac{1}{100};$$ $$2(n-3) > 100;$$ $$n — 3 > 50, \text{ отсюда } n > 53;$$

Ответ: $n = 54$.

Пусть $y(n) = \frac{C_n^3}{A_{n-1}^3}$, где $n \geq 4$.

а) Дробно-линейная функция, которой принадлежат точки $(n; y(n))$:

Рассмотрим выражение для $y(n)$:

$$y(n) = \frac{C_n^3}{A_{n-1}^3}$$

Здесь $C_n$ и $A_{n-1}$ — это биномиальные коэффициенты, которые можно выразить через факториалы.

Разложим биномиальные коэффициенты:

$$C_n = \binom{n}{3} = \frac{n!}{3!(n-3)!}$$

и

$$A_{n-1} = \binom{n-1}{3} = \frac{(n-1)!}{3!(n-4)!}$$

Подставим эти выражения в формулу для $y(n)$:

$$y(n) = \frac{\left( \frac{n!}{3!(n-3)!} \right)^3}{\left( \frac{(n-1)!}{3!(n-4)!} \right)^3}$$

Упростим дробь:

$$y(n) = \frac{\frac{n!^3}{(3!)^3 (n-3)!^3}}{\frac{(n-1)!^3}{(3!)^3 (n-4)!^3}}$$

Учитывая, что $(3!)^3$ сокращается, получаем:

$$y(n) = \frac{n!^3}{(n-3)!^3} \cdot \frac{(n-4)!^3}{(n-1)!^3}$$

Упростим выражение дальше:

$$y(n) = \frac{n!}{(n-1)!} \cdot \frac{(n-4)!}{(n-3)!}$$

$\frac{n!}{(n-1)!} = n$ и $\frac{(n-4)!}{(n-3)!} = \frac{1}{n-3}$, следовательно:

$$y(n) = \frac{n}{6(n-3)}$$

Таким образом, дробно-линейная функция, которой принадлежат точки $(n; y(n))$, имеет вид:

$$y = \frac{x}{6(x-3)}$$

где $x$ — это переменная, вместо $n$.

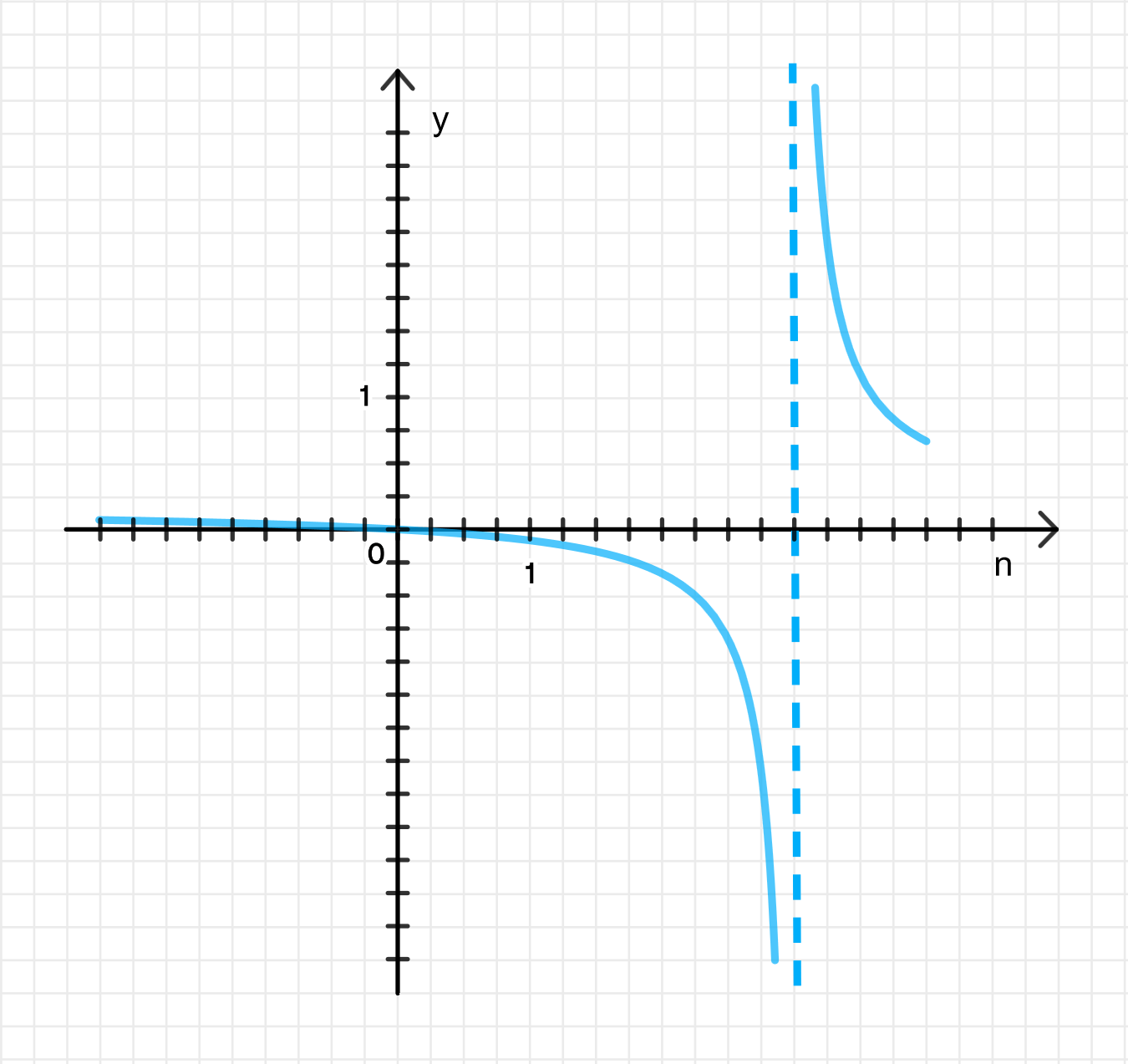
б) Построение графика функции:

Теперь давайте определим ключевые моменты для построения графика функции $y(x) = \frac{x}{6(x-3)}$.

Область определения:
Функция определена при $x \neq 3$, так как в точке $x = 3$ знаменатель обращается в ноль. Таким образом, $x = 3$ — это асимптота функции.

Предел при $x \to \infty$:
Рассмотрим предел функции при $x \to \infty$:

$$\lim_{x \to \infty} \frac{x}{6(x-3)} = \frac{1}{6} \cdot \lim_{x \to \infty} \frac{x}{x-3} = \frac{1}{6} \cdot 1 = \frac{1}{6}.$$

Таким образом, горизонтальная асимптота функции — это линия $y = \frac{1}{6}$.

Поведение функции около точки $x = 3$:
Когда $x$ стремится к 3 с левой стороны, значение функции стремится к минус бесконечности, а когда $x$ стремится к 3 с правой стороны — к плюсу бесконечности. Таким образом, $x = 3$ — вертикальная асимптота.

Примерные значения функции:
Подставим несколько значений $x$ в функцию $y(x)$:

в) Наибольшее число $n$, при котором $y(n) > 0.25$:

Необходимо решить неравенство:

$$\frac{n}{6(n-3)} > 0.25$$

Умножим обе стороны на $6(n-3)$ (при условии, что $n > 3$):

$$n > 0.25 \cdot 6(n-3)$$

Упростим правую часть:

$$n > 1.5(n-3)$$

Раскроем скобки:

$$n > 1.5n — 4.5$$

Переносим все слагаемые с $n$ в одну сторону:

$$-0.5n > -4.5$$

Разделим обе стороны на $-0.5$ (не меняя знака неравенства):

$$n < 9$$

Таким образом, наибольшее $n$, при котором $y(n) > 0.25$, равно $n = 8$.

г) Наименьшее $n$, при котором $y(n)$ отличается от $\frac{1}{6}$ менее, чем на 0.01:

Нужно решить неравенство:

$$\left| \frac{n}{6(n-3)} — \frac{1}{6} \right| < 0.01$$

Упростим выражение:

$$\left| \frac{n}{6(n-3)} — \frac{1}{6} \right| = \left| \frac{n — (n-3)}{6(n-3)} \right| = \left| \frac{3}{6(n-3)} \right| = \frac{1}{2(n-3)}$$

Неравенство принимает вид:

$$\frac{1}{2(n-3)} < 0.01$$

Умножим обе стороны на $2(n-3)$:

$$1 < 0.02(n-3)$$

Разделим обе стороны на 0.02:

$$50 < n-3$$

Следовательно:

$$n > 53$$

Таким образом, наименьшее $n$, при котором $y(n)$ отличается от $\frac{1}{6}$ менее, чем на 0.01, равно $n = 54$.

Ответы:

а) $y = \frac{x}{6(x-3)}$.

б) Построен график функции.

в) Наибольшее $n$, при котором $y(n) > 0.25$, равно $n = 8$.

г) Наименьшее $n$, при котором $y(n)$ отличается от $\frac{1}{6}$ менее, чем на 0.01, равно $n = 54$.